|
||||||||||||||||||||||||||||||||||||
![]()
|
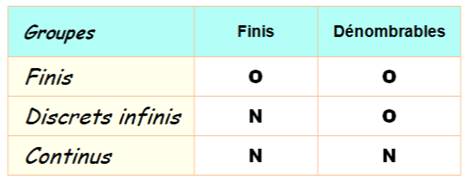
TYPES DE GROUPES
|
|
|
|
|
|
|
|
|
|
|
Exemple: racines quatrièmes
de l'unité G = {+ 1, – 1, + i, – i} avec multiplication + i = (+ i)1, − 1 = (+ i)2, − i = (+ i)3, 1 = (+ i)4 Élément générateur: aussi bien + i que – i.
Groupes de permutations ou de symétries Les permutations
déplacent les n éléments de toutes les façons possibles, soit n! (factorielle n) possibilités.
Toutes ces possibilités forment le groupe des permutations Sn.
Voir Exemple
Voir Développements Groupes alternés Le groupe alterné de degré n, noté An, est un
sous-groupe de permutations composé des éléments résultant d'une quantité
paire de transpositions. Utilisé pour démontrer la résolution du taquin ou du cube de Rubik. A4 laisse invariant le tétraèdre et dodécaèdre
réguliers; A5, l'icosaèdre. Groupes simples finis exceptionnels au nombre de 26 en tout et pour tout, dont le
Monstre. Voir historique
de leur découverte Groupes simples finis, familles de groupes de
transformations liées à l'algèbre linéaire, comme les groupes linéaires
(espaces vectoriels). |
|
|
du triangle équilatéral
– S3 |
|
|
Le triangle equilateral présente six cas de symétries:
Le groupe de symétrie du triangle équilatéral est isomorphe à S3.
Il est d'ordre 6 et non-commutatif (non-abélien). Suite en Groupes de permutation |
|
|
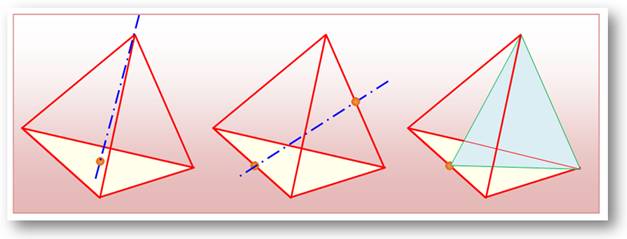
du tétraèdre – S4 |
|
|
Le tétraèdre présente 24 cas de
symétries:
Ces transformations
(symétries) effectuent toutes les permutations des quatre sommets. Le groupe de symétrie du tétraèdre est isomorphe à S4. Il
est d'ordre 24 et non-commutatif (non-abélien). |
|
|
des polygones réguliers
– Dn |
|
|
Le polygone régulier à n
côtés présente 2n cas de symétries. C'est une généralisation du cas du
triangle.
Par exemple: le pentagone
régulier appartient aux groupe D5. Il présente 10 cas de
symétries: cinq rotations et cinq
réflexions. Le groupe de symétrie du polygone régulier à n côtés est noté Dn.
Il est non-commutatif (non-abélien). Suite en Groupes de permutation / Équation quintique |
|
|
|
|
|
Ce sont par exemples tous
les groupes arithmétiques qui souvent sont plus que groupe: anneaux ou corps. Suite en Groupes de nombres |
|
|
|
|
|
Ce sont par exemple:
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Outils/Outils/Structur/GrCycliq.htm
|
![]()