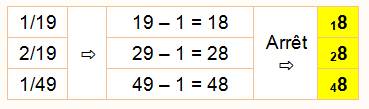|
|||||||||||||||||||||||||||||||||||
|
CALCUL VÉDIQUE de 1/..9 Les Indiens anciens avaient
des méthodes rapides de calcul de
cette fraction unitaire dont le dénominateur est terminé par 9. Il est vraisemblable que vous n'utiliserez
jamais cette méthode de calcul. Pourtant, lisez cette page
pour vous rendre compte comme le monde des nombres est fascinant. Après un
exposé de la méthode, on expliquera pourquoi ça marche. Puis on généralisera
la méthode de calcul. |
|
Concerne
le nord de l'Inde. Période:
- 2000 à – 500. Écriture
des textes védas, hindouistes, en sanscrit védique. Formation
des royaumes de l'Inde ancienne. À
partir de 320 av. J.-C viendra l'âge d'or de l'hindouisme et de la
littérature sanskrite classique. |
D'après Wikipédia
|
|
|||
|
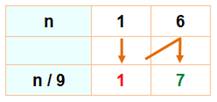
Observation Aviez
vous remarquez que la division par 9 d'un nombre de deux chiffres est immédiate:
|
16 = 1 x 9 + 7 52 = 5
x 9 + 7
57 = 6 x 9 + 3 |
||
|
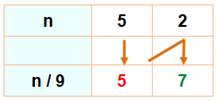
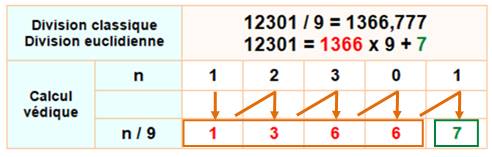
Avec la
méthode védique la division par 9 est particulièrement rapide. Partant
de la gauche vers la droite, elle est réalisable mentalement. Le second
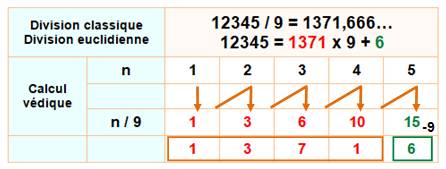
exemple montre le traitement des retenues, en prenant soin de retirer 9 (et
non pas10) au reste. |
Chiffre = somme
du précédent avec celui du dessus Un premier
fictif est à 0; le dernier est le reste.
|
||
Voir Nombre 9 /
Divisibilité
par 9 / Preuve
par 9 / Brève
559
|
|
|
|
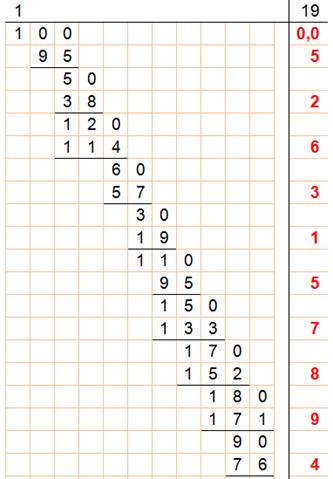
Comment
calculer une fraction comme 1/19? Observation
La seconde
partie ajoutée à la première donne un résultat composé de 9. Principe On
introduit ici une notation indienne qui indique que le cycle des décimales
est terminé. Ainsi, " i " veut dire que le prochain
chiffre est 1 et que le cycle des mêmes décimales se répète. Actuellement, on
signale cette répétition des décimales en les surlignant. A ce
niveau la division donne un quotient égal à 1 et un reste égal à 1. Puis, on
repart avec la division 1/19 comme au début. |
|
Voir Nombre
1/19 = 0,0526…
Voir Division
décimale
|
|
||
|
Première étape: chiffre de calcul Dans 19,
on prend le 1 et on lui ajoute 1 qui donne 2,
le chiffre du calcul. Deuxième étape: itérations |
||
|
Le dernier
chiffre du cycle sera 1. |
1 |
|
|
Le suivant
sera ce dernier multiplié par 2. |
2
1 |
|
|
On
continue à multiplier par 2 le chiffre de
gauche. |
4
2 1 |
|
|
Idem. |
8
4 2 1 |
|
|
Encore,
mais en faisant attention à la dizaine 2x8=16. |
1
6 8 4 2 1 |
|
|
Insistons,
poursuivons... en prenant la retenue 2x3+1=13. |
1
3 1 6 8 4 2 1 |
|
|
On
multiplie et on prend la retenue. |
7
1 3 1 6 8 4 2 1 |
|
|
On
s'arrête lorsqu'on retrouve le " 1 " du début. 1
1 0 5 1 2 6 3 1 1 1 5 1
7 1 8 9 1 4 7 1 3 1 6 8 4
2 1 1/19 = 0,052631578947368421 … |
||
|
Notez qu'on peut facilement écrire le résultat d'un seul
trait, en écrivant de droite à gauche. |
||
|
|
|
|
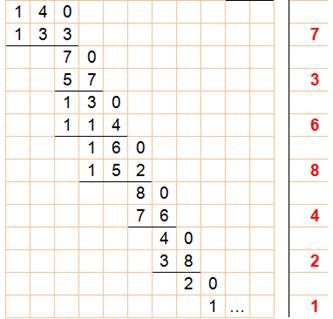
Dans ce
cas on prend le 2 de 29, on lui ajoute 1; le chiffre du calcul sera 3. On procède
comme ci-dessus en multipliant par 3.
1/29 = 0,0344827586206896551724137931 034 … |
|
Voir Nombre
1/29 = 0,0344…
Voir Tables – Index
|
|
|||
|
Type de fractions |
Le dénominateur
est un nombre premier, et |
Exemple: 1/19 |
|
|
Valeurs
de références |
1) n
= dénominateur (D) – 1 2) m
= n/2 3) x
= dizaines de D + 1 |
n = 18 m =
9 x =
2 |
|
|
Initialisation |
4) Décimale
d = 1 |
d = 1 N = …1 |
|
|
Calculs
itératif |
5) Multipliez
d par x. 6) S'il
y a une retenue, la conserver pour l'ajouter au coup suivant. |
d = 1 x 2 = 2 N = … 21 r = 0 |
|
|
7) Faites
ces opérations m fois. 8) Prenez
son complément à 9. |
N
= …947368421 => 052631578 |
||
|
Finalisation |
9) Concaténez
et placez la virgule. |
N
= 0,052631578 947368421 … |
|
Voir Algorithmes
Période maximale
|
La
période maximale d'un
nombre par un nombre premier P est égale à P – 1. En effet, tous les restes
possibles de la division par 19 sont épuisés après au maximum 18 essais. La
division suivante donne un reste déjà connu et, avec lui, la suite des
divisions déjà connues. |
|
|
||
|
Deux
phénomènes |
L'effet d'une série géométrique Une sorte de reconstitution d'un
nombre décimal. |
|
|
(r0 = 1 a été placé à droite) |
|
|
|
Avec r
< 1 |
|
|
|
Supposons
que le rationnel x/y soit cette limite |
|
|
|
Si ce
nombre est 1/19 |
|
|
|
Reprenons
S |
|
|
|
Mise en
évidence des puissances de 10 |
|
|
|
Nous
reconnaissons la numération décimale |
|
|
|
Parallèle
montrant les décimales de 19, aux retenues près. |
|
|
|
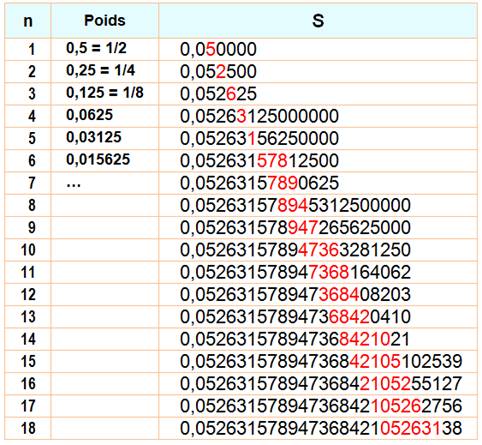
Construction de la série Le premier
terme (n = 1) a
Ce qui donne un premier terme égal à
1/20 = 0,05. Le premier chiffre est
5. Le
deuxième a un poids de 0,25 en position 1/100 soit une valeur de 0,0025, qui
ajouté au premier donne un cumul de 0,0525. La suite
des chiffres se construit progressivement de cette manière jusqu'à 19 – 1) 18
itérations. |
|
|
|
Finale en 1 |
Remarquez que Période x Dénominateur
= 999 …9 Ex:
pour 1/7: 0,142857 x 7 = 0,999 999… = 1 En
fin de période, le reste revient au 1 initial du numérateur. Voir Exemple de la division par 7. |
|
|
Sans
surprise, la règle est généralisable. Tout
nombre rationnel est exprimable sous la forme d'une série géométrique
infinie. Transformons
la fraction en mettant en évidence une puissance de 10, puis une terminaison
en 9:
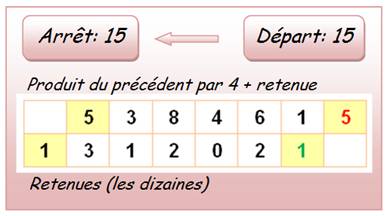
Le
départ est 15 et le multiplicateur est 4. Soit la suite des opérations:
La
suite des décimales est 38461 et en tenant compte du 1/10: 1/26 = 0,038461 38461 … |
|
Suite |
|
|
Voir |
|
|
Livre |
Ce livre acheté à
NewDehli en 1998 m'avait coûté 125 roupees (1,6 euro). |
|
Site |
|
|
Cette page |
