Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/12/2021 M'écrire Brèves de Maths

INDEX Triangles Géométrie Opérations sur les puissances	Théorème de Pythagore - Démonstrations
	Débutants	Nomenclature – Types de démonstrations		Applications
	Toute figure	Approche	Calcul Aires	Dissections
	Triplets de P.	Historiques	Similitudes	Hypoténuse
	Pappus-Clairaut	Chinoise (Chou Pei)	Algébrique	Pyramide

Théorème de Pappus-Clairaut Une généralisation du théorème de Pythagore aux parallélogrammes associés aux côtés d'un triangle quelconque.
	Sommaire de cette page >>> Théorème de Pappus-Clairaut >>> Théorème de Pythagore >>> À partir du théorème de Pythagore	Débutants Géométrie Glossaire Géométrie

Anglais: Pappus Area Theorem

Voir Types de démonstrations du théorème de Pythagore

Théorème de Pappus-Clairaut		haut
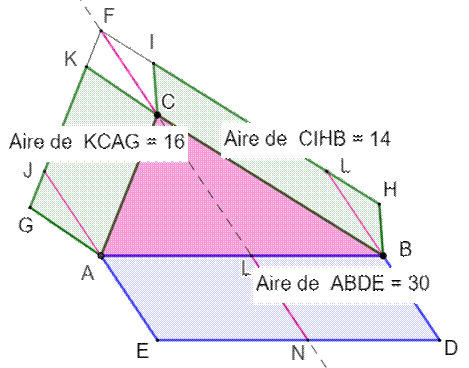
Construction Triangle ABC. Parallélogramme bleu (ABDE). Parallèle en C à AE. Point F tel que: FC = AE = BD Parallèles en F à AC et à BC. Choix de K et I sur ces parallèles. Parallélogrammes verts (KGAC et ICBH). Théorème Aire du parallélogramme bleu = Aire des parallélogrammes verts. Historique Pappus présente cette propriété en prenant le parallélogramme AJLB en haut, et non celui du bas. Le théorème, en France, est attribué à Clairaut, frère du célèbre mathématicien. C'est Ozanam qui en aurait retrouvé l'origine chez Pappus.
Démonstration Aires des parallélogrammes verts	Aire KCAG = Aire FCAJ = idem pour tout point K, car la longueur de la base FJ = KG est constante, et la hauteur entre les parallèles GF et AC est constante. Aire ICBH = Aire FCBL = idem pour tout point I, et cela pour les mêmes raisons.
Aires du parallélogramme bleu = deux composantes = ALNE + LBDN	Les aires côté gauche sont égales: Aire LNEA = Aire FCAJ: bases LN et CF égales, et hauteurs entre les parallèles FN et JE sont égales. Les aires côté droit sont égales pour les mêmes raisons.
Rapprochement	Aire ALNE = Aire AGKC Aire LBDN = Aire BCIH Aire ABDE = Aire AGKC + Aire BCIH.

Merci à François Boucher pour ses remarques

Vers théorème de Pythagore		haut
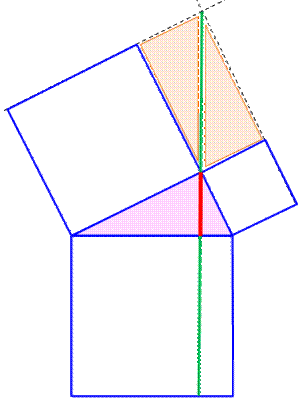
Propriété Le théorème de Pythagore est un cas particulier du théorème de Pappus-Clairaut. Conditions: le triangle rose est rectangle, et les parallélogrammes sont des carrés. On retrouve bien une longueur égale pour les deux segments en vert. Application du théorème de Pappus-Clairaut: Aire des deux carrés du haut = aire du carré du bas. Voir Propriétés de cette figure

À partir du théorème de Pythagore		haut
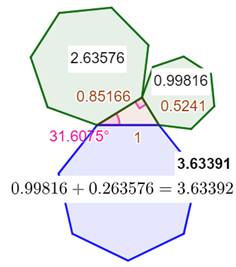
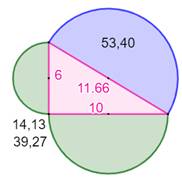
On sait démontrer le théorème de Pythagore sans le théorème de Pappus-Clairaut. Alors, dans un triangle rectangle, on a : a² + b² = c²; et plusieurs résultats en découlent. Polygones réguliers Tout triplet de polygones réguliers avec côté a, b et c est tel que la somme des aires des deux plus petits vaut l'aire du plus grand. Exemple avec ces trois heptagones: la relation entre les aires est bien celle attendue. 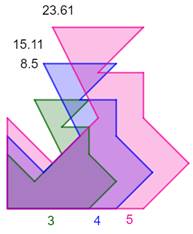Le cas des demi-cercles apposés aux côtés du triangle rectangle est bien connu. Figures semblables Soit deux figures semblables de rapport homothétie k, alors les aires sont dans le rapport k². Dans le cas du triangle rectangle apposer trois figures semblables dans les proportions des longueurs des côtés, créera trois figures dont la somme des aires des deux plus petites vaudra l'aire de la plus grande. Voir Application du théorème de Pythagore à tout triplet de figures semblables Autres figures Voir le cas des triangles quelconques >>> Voir le cas des triangles parallélogrammes >>>

Merci à Alain Goupil pour cette suggestion

Haut de page

Retour	Théorème de Pythagore
Suite	Démonstrations historiques du théorème de Pythagore
Voir	Théorème de Pappus
Sites	Théorème de Clairaut (géométrie) – Wikipédia Voir liste des liens
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/Pappus.htm