|
Édition du: 15/01/2020 |
|
INDEX |
Géométrie – RECTANGLES |
||
![]()
|
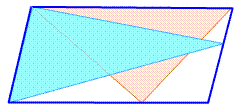
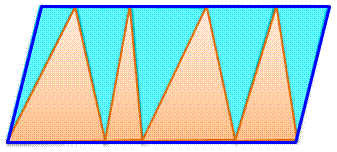
Parallélogramme DIVISÉ en TRIANGLES
Propriétés
concernant l'aire des triangles inscrits dans un parallélogramme. Objet d'une
fameuse énigme réputée difficile. Sur
cette figure: Aire bleue = Aire
ocre = ½ Aire parallélogramme |
||
|
|
Sommaire de cette page >>> Parallélogramme
dans parallélogramme >>> Moitié de parallélogramme >>> Quart de parallélogramme >>> Trois triangles et plus >>> Énigme |
Débutants Glossaire |
|
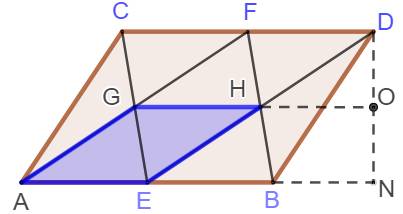
Problème Un
parallélogramme ABDC. Les points milieux E et F et les segments les reliant
aux sommets. Démontrer
que le quadrilatère AEHG est un parallélogramme. Solution Quadrilatère AEDF: AE est parallèle à DF et AE =
FD: c'est un parallélogramme et AG est parallèle à EH. Les quadrilatères AEFC et EBDF sont des
parallélogrammes égaux (homothétiques); leurs diagonales sont de même
longueur et se coupent en leur milieu: AG = EH. Avec AG parallèle à EH et AG = EH, le
quadrilatère AEHG est un parallélogramme. |
|
|
|
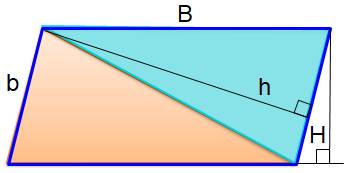
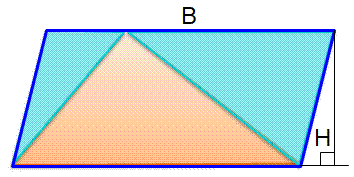
Partage par une diagonale Chacune
des diagonales du parallélogramme le divise en deux parties d'aires égales. Pour
chacun des deux triangles les bases (B) sont égales et ils ont même hauteur (H);
les aires sont égales. Valable dans l'autre sens. Aire parallélogramme = B.H = b.h Aire triangle ocre = ½ B.H = ½ b.h Aire triangle bleu = ½ B.H = ½ b.h |
|
|
|
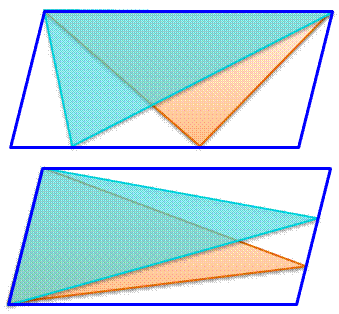
En conservant la base Si la
base est conservée et que le troisième sommet se déplace sur l'autre côté du parallélogramme,
la hauteur est conservée et avec elle, l'aire du triangle. Sur ces figures, et quelle que soit la position
du sommet sur l'autre côté du parallélogramme, les aires valent la moitié de celle du parallélogramme. |
|
|
Voir Aire du
parallélogramme – Introduction et développements
|
Partage par les deux diagonales Les
traits pointillés partagent le parallélogramme en moitié dans un sens ou
l'autre. Pour
chacun des triangles, les bases sont conservées et la hauteur à été divisée
par deux. Aire parallélogramme = B.H = b.h Aire d'un triangle ocre = ¼ b. h/2 = ¼
b.h Aire d'un triangle bleu = ¼ B. H/2 = ¼ B.H Même
constat en prenant chaque quart de parallélogramme et leurs diagonales. |
Sur cette figure,
l'aire de chacun des triangles est égale au quart
de celle du parallélogramme. |
|
|
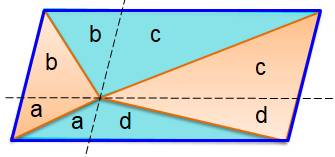
Partage à partir d'un point interne Les
traits pointillés partagent le parallélogramme en huit triangles égaus deux à
deux (effet de la diagonale des petits parallélogrammes). Aire ocre = a + b + c + d Aire bleue = b + c+ a + d Aire ocre = aire bleue = ½ aire du
parallélogramme |
|
|
Voir Partage
du parallélogramme
|
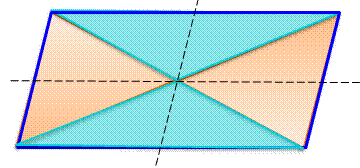
Partage par deux sécantes On a vu
que l'aire du triangle ocre vaut la moitié de celle du parallélogramme
complet. Par
différence, celle des deux triangles bleus vaut également la moitié. Aire bleue = Aire ocre = ½ Aire parallélogramme |
|
|
|
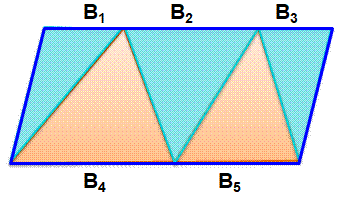
Partage par trois sécantes Aire des
trois triangles bleus: Aire bleue = ½ B1.H + ½ B2.H
+ ½ B3.H Aire des
deux triangles ocre: Aire ocre = ½ B4.H + ½ B5.H
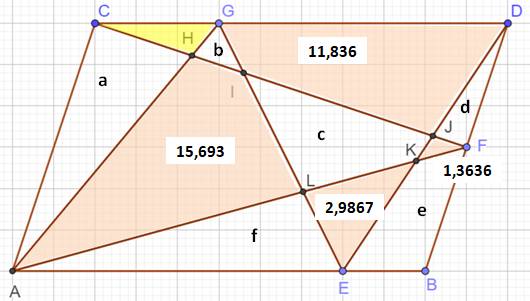
= ½ B.H Sur de telles figures: |
|
|
|
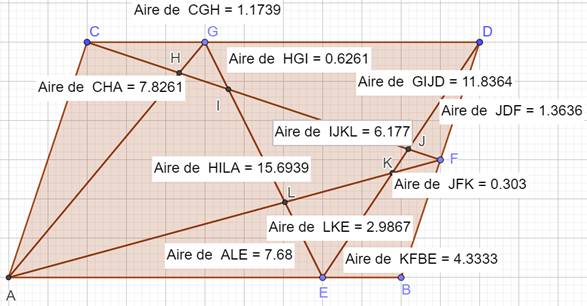
Avec ces seules données
(aires), déterminer l'aire du triangle jaune. Le problème semble impossible à résoudre avec si peu d'informations. Pensez aux propriétés vues ci-dessus et la solution devient presque
évidente. |
|
|||
|
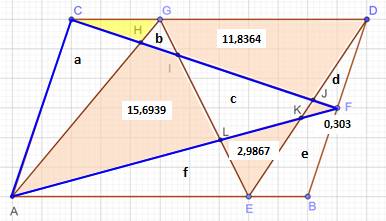
Solution Avec le
triangle bleu A/2 = a + 15,6939 + c + 0,303 Avec les
triangles rouges: A/2 = x + a + 11,8364 + c + 2,9867 En
rapprochant ces deux égalités a + 15,6939 + c
+ 0,303 = x + a +
11,8364 + c + 2,9867 Les aires
a et c disparaissent, laissant une valeur numérique pour x: x = 15,6939 + 0,303
– 11,8364 – 2,9867 x = 1,1738 |
|
|||
|
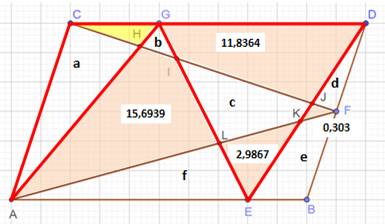
Figure complète pour information La valeur calculée pour x est confirmée par GeoGebra: x = 1,1739 à l'arrondi près. |
|
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |