|
|||||||||||||||||||||||||||||||||||
![]()
|
Construction du DODÉCAGONE Le dodécagone
est un polygone à douze côtés.
|
|
CONSTRUCTION
du dodécagone régulier à
partir d'un hexagone |
|
|
Vous
savez construire l'hexagone.
Tracez des carrés sur les
côtés. Joignez
les sommets extérieurs de ces carrés.
|
|
|
CONSTRUCTION du dodécagone régulier avec
un carré |
|
|
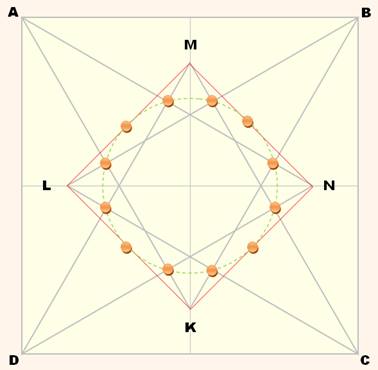
Construire un carré. Construire les quatre triangles équilatéraux sur les côtes
du carré.
Dessiner
le carré ayant pour sommets les pointes des triangles équilatéraux. Tracer
les milieux
des côtés de ce dernier carré. Joindre
les points comme indiqués sur la figure et le dodécagone est construit. En
prenant un sommet sur deux, on construit l'hexagone. Autre
présentation (avec repérage par lettres)
Marquer
le milieu des quatre segments du type LM. Repérez
le milieu des huit
segments du type AK. Ces
douze points sont les sommets d'un dodécagone Voir Démonstration |
|
|
|
|
|
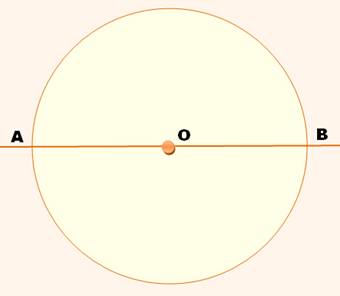
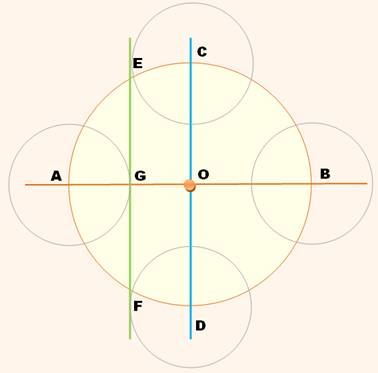
Construire une droite
et un cercle
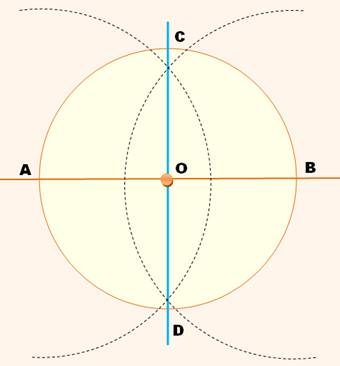
Construire la médiatrice de AB avec deux
arcs de cercle de centre A et de centre B avec une ouverture du compas
supérieure à AO. La médiatrice (en bleu) coupe le cercle en C et D.
Construire le cercle de centre A de rayon AO. Il coupe le cercle en E et F; tracer la droite EF
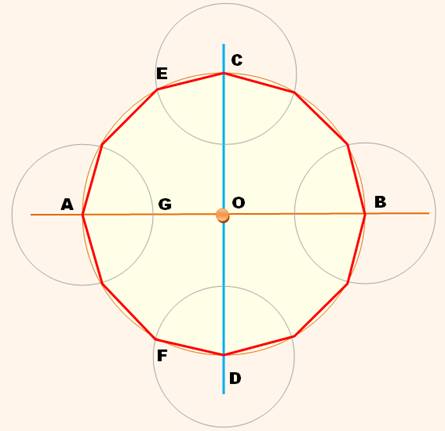
(médiatrice de AO) qui coupe AO en G. Construire le cercle de centre A de rayon AG. Puis la même chose en B, C et D. Les centres des petits cercles et leurs intersections
avec le grand cercle forment les sommets du dodécagone:
Principe Pour construire l'hexagone (6 côtés), il faut
diviser le cercle en six avec des
cercles de rayon unité. Pour le dodécagone (12 côtés), il faut diviser le
cercle en douze avec des cercles de rayon un demi.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()