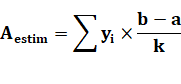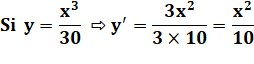|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
Humour
|
Deux mathématiciens au restaurant s'interrogent
sur la connaissance en maths de la population. Le niveau moyen est tristement faible,
dit l'un. Mais, non ! dit l'autre. Ils en viennent à parier le prix du repas,
en prenant la serveuse comme cobaye. Pendant que le premier se rend aux
toilettes, le second dit à la serveuse: - Vous aurez 50 euros si vous
répondez "un tiers de x au cube" à la question que je vous poserai. L'autre rentre et le premier apostrophe la
serveuse: - dites-moi, jeune demoiselle, savez-vous qu'elle est l'intégrale
de x au carré ? La serveuse réfléchit, tourne la tête et finalement énonce:
"un tiers de x au cube". Le perdant bon joueur admet qu'il doit
payer le repas. La serveuse quitte les deux mathématiciens en
murmurant: - il ne faut oublier la constante ! |
|
|
Avec le lait comme base:
|
|
Voir Pensées et Humour
|
Intégration – Approche
Calcul intégral ou intégration, c'est quoi en un mot ? Simplement,
un calcul de surface ! Oui, mais dans des cas un peu
problématiques comme la surface sous une tranche de parabole ou comme l'aire
de la partie ocre sous la courbe de la figure. |
Voir Découverte
progressive du calcul intégral
|
|
||
|
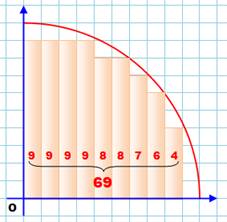
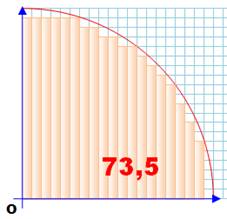
Méthode classique Elle consiste à comparer l'aire à estimer avec
des surfaces d'aire connue, comme ici avec des bandes rectangulaires
verticales. Exemple Avec un quart de cercle de rayon 10, l'aire est
connue: Pi x 10² / 4 = 78,54. Mais sans cette connaissance, comment l'évaluer
? En haut, l'aire est encadrée par une valeur
minimale (69) et une valeur maximale(85). Une bonne estimation consiste à
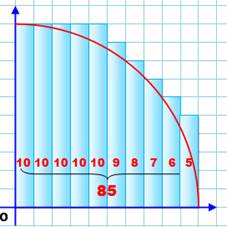
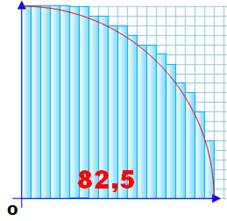
prendre la moyenne: (69 + 85) / 2 = 77. En prenant des bandes plus fines (deux fois plus
petites, en bas), l'aire minimale devient 73,5 et maximale 82,5; pour une
moyenne de 78. En prenant des bandes de plus en plus fines,
l'aire estimée converge vers l'aire réelle. |
Notez que plus la bande verticale
est fine et plus elle sont voisine de la bande moyenne. |
|
Voir Méthode
d'Archimède pour la parabole / Algorithme
d'Archimède pour le cercle (Pi)
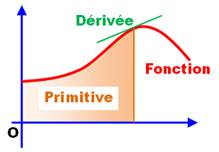
Dérivée
et intégrale: une explication simple et rapide
|
Air sous la
courbe = Intégrale |
|||
|
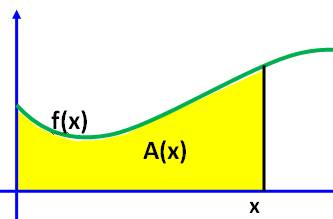
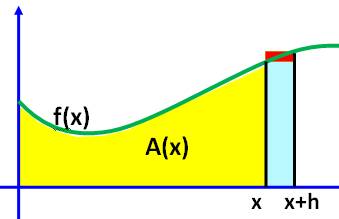
Question Pourquoi l'intégrale
représente l'aire sous la courbe (en jaune), alors que la dérivée est la
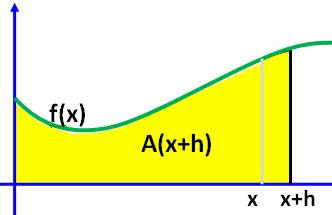
pente ? Réponse La figure est complétée pour obtenir une surface
jaune légèrement supérieure. Nous allons évaluer l'augmentation de l'aire
A(x+h) – A(x) par encadrement.
Encadrement
En divisant par h, non nul:
Voyons pour h de plus en plus petit. Alors l'expression centrale
correspond à la définition de la dérivée A'(x):
|
|
||
|
Passage à la limite:
Conclusion
|
La dérivée est bornée par la même quantité f(x) à
droite et à gauche. Elle est égale à cette borne: A'x = f(x). Alors:
|
||
|
|
|||
|
Après avoir noté comment estimer l'aire d'une
surface complexe, voyons comment exprimer le calcul. Surface de calcul On souhaite connaitre l'aire sous la courbe
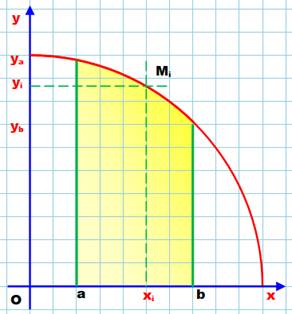
depuis l'abscisse a jusqu'à b. Pour ces deux abscisses, la courbe se situe aux
ordonnées ya et yb et, d'une manière générale un point Mi
d'abscisse xi se trouve à l'ordonnée yi. Caractérisation des rectangles En décidant de prendre k bandes fine entre a et b,
la largueur de la bande est égale à (b – a ) / k et la hauteur de la bande
moyenne en xi est yi. L'aire d'un rectangle devient:
Somme des aires A = somme des aires de toutes les bandes. |
|
||
|
Calcul discret (= discontinu) |
|
||
|
Calcul continu (passage à la
limite) L'aire réelle sera atteinte lorsque les bandes
seront les plus fines possibles, idéalement d'épaisseur nulle; c'est la
notion de limite. La notation introduit le symbole "porte-manteau"
en indiquant la plage de calcul (a et b) et en adoptant le symbole dx pour
indiquer que les bandes ont une largeur dx très fine. Avec la connaissance de l'équation de la courbe (le cercle
dans notre exemple), il est possible de développer une technique de calcul
qui donnera directement l'aire sous la courbe. Cette technique s'appelle le calcul intégral. Le symbole en
'porte-manteau" est appelé signe somme, signe d'intégration, signe
intégral ou intégrateur; il a été introduit par Leibniz. |
Général
Équation du cercle et intégrale
|
||
Résumé: intégration et primitive
|
L'aire sous une courbe peut être estimée par un pavage de bandes fines
rectangulaires. La valeur estimée est d'autant plus proche de la valeur
réelle que les bandes sont fines. La technique d'intégration résulte d'un
passage à des bandes d'épaisseur mathématique nulle. Un passage à la limite qui se prête à une technique opératoire
appelée intégration et faisant appel à la primitive d'une fonction. La primitive étant en quelques sorte la dérivée inverse d'une fonction; dit-autrement:
connaissant la dérivée retrouver la fonction. |
|
|
||
|
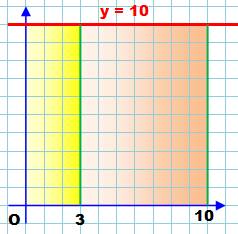
Aire du rectangle avec la méthode
d'intégration Il s'agit de calculer l'aire pour la droite
d'équation y = 10 dans deux cas: aire en jaune et aire en ocre. L'équation est connue y = 10. Nous devons connaitre la primitive, inverse de la
dérivée. Autrement dit: quelle est la fonction qui donne la constante 10
comme dérivée
?
La règle du calcul pratique dit que: L'aire cherchée est égale à la différence entre
les valeurs de la primitive au deux bornes de la plage.
|
Le calcul par intégration restitue bien les
valeurs classiques des aires des rectangles: Jaune: 3 x 10 = 30 Ocre: 7
x 10 = 70 |
|
|
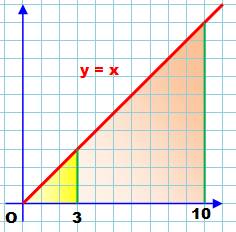
Aire du triangle
|
Jaune: ½ (3 x 3) = 4,5 Ocre: ½
(10 x 10) – 4,5 = 45,5 |
|
|
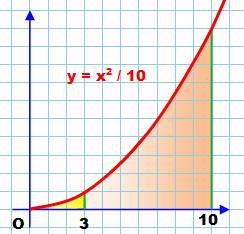
Aire du segment de parabole
|
|
|
Voir Brève
769 / Autre exemple de calcul par
intégral avec y = x²
|
Si nous connaissons les dérivées nous
pouvons en déduire les primitives correspondantes et, en appliquant la
méthode proposée (non justifiée à ce niveau d'initiation), nous pouvons
calculer l'aire sous une courbe quelconque dont nous connaissons l'équation. La méthode ne marche, évidemment, que si la
courbe varie régulièrement (la fonction est continue). Et après … À ce niveau d'explication, la notion
d'intégration est relativement simple. Son usage devient vite un casse-tête
pour des fonctions plus élaborées et, surtout, pour les calculs comportant
plusieurs niveaux d'intégration (calcul de volumes et plus). Mais, pas moyen
d'y échapper, c'est le seul outil vraiment efficace pour un grand nombre de
problèmes: là où on connait le comportement local ou instantané et que l'on
veut en déduire le comportement général. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Analyse/Primitiv/IntAppro.htm
|
![]()