|
|||||||||||||||||||||||||||||||||||
![]()
|
INTRODUCTION
Les exponentielles, des fonctions mathématiques que
vous retrouvez dans la croissance du
nénuphar ou le calcul de vos intérêts à la banque. |
|
||||||
|
Une
bestiole se dédouble toutes les secondes et remplit la boite de culture en
une minute. La laborantine en place quatre dans la boite. Combien de temps
pour remplir la boite? |
|
|
||
Alternative
|
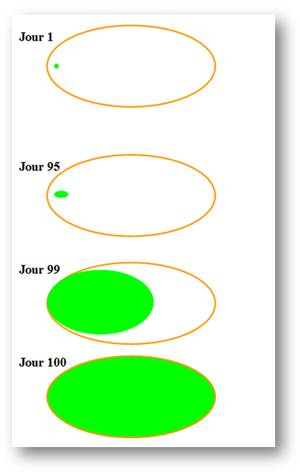
Le
nénuphar double sa surface tous les ans. À la vingtième année, il couvre toute
la nappe d'eau. Si on avait mis deux nénuphars au départ, quand aurait été
recouverte la nappe d'eau. Dix-neuf ans, bien entendu. Il recouvre chacun la
moitié. l'année précédente, il recouvrait chacun le quart. |
|
P
double de surf ch
|
|
|
1 pour mille
Rien durant 9/10 du
temps
|
Voir Vitesse
|
|
||||||||||
|
|
|
|||||||||
|
|
Voir Dérivée |
|||||||||||||||
|
|
Voir
"e" et la banque |
||||||||
|
de
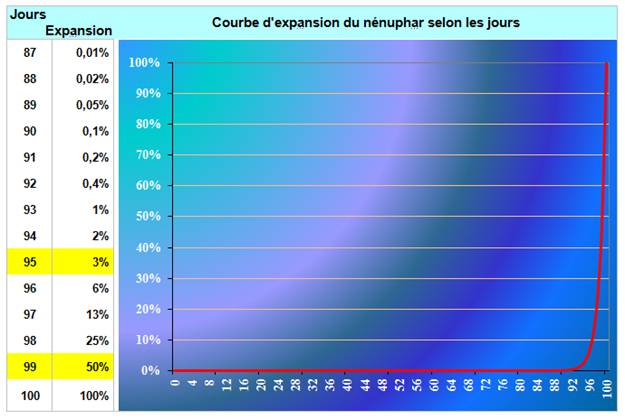
croissance du nénuphar |
|
|
Paramètres
Valeur de y y100 = 1 y99 = 1/2
y0 = T y1 = 2 T y2 = 22 T yn = 2n T
T = 1/ 2100 = 1/ 1,26 1030
= 7,88 … 10-31 Équation de croissance
du nénuphar y = 7,88 10-31 . 2x
y =
7,88 10-31 . e 0,69 x Pour info: ln(2)
= 0,69314718055994530942… T = 1 / 2100 = 1 /
1267650600228229401496703205376 |
|
Car:
2 x 299 = 21 x 299 = 21 + 99 = 2100 |
||||||
|
Question Une
bestiole se dédouble toutes les secondes et remplit la boite de culture en
une minute. La laborantine en place quatre dans la boite. Combien de temps
pour remplir la boite? Réponse En
prenant le processus par le début:
Le
temps de remplissage est donc 60 – 2 = 58 s |
|
Dans
l'Écume des Jours, la chambre où se meurt peu à peu Chloé rétrécit à mesure
que grandit dans son poumon le nénuphar qui
la tue. |
Voir Poésie
![]()
|
Suite en |
|
|
|
|
|
Livre |
|
|
Cette page |
![]()