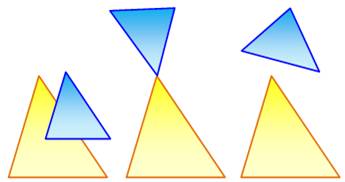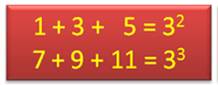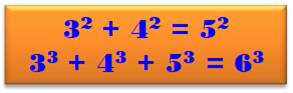NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 6

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

100. Parité des puissances
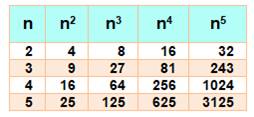
Pour toutes les puissances Un nombre et ses puissances sont de même parité. Nombre pair 2a: (2a)^k = 2^k . a^k Un nombre comprenant une puissance de 2 est divisible par 2; cette puissance est paire comme le nombre dont elle est issue. Nombre impair 2a + 1: (2a + 1)^k = A + 1 Malgré l'élévation à une puissance le 1 final persiste; le nombre porté à la puissance k reste impair comme le nombre.		Exemples Avec de l'algèbre Calcul de la différence entre N^k – N en utilisant une identité remarquable: N^k – N = N (N^k – 1 – 1) = N (N – 1) . M La différence est divisible par le produit de deux nombres consécutifs. L'un d'eux est pair. La différence est bien divisible par 2.
Pour en savoir plus	>>> Nombres pairs et nombres impairs >>> Puissance des nombres >>> Puissances de 2		>>> Développement de n^k – n >>> Identités remarquables >>> Divisibilité de produits

101. Trois infinis ou deux?
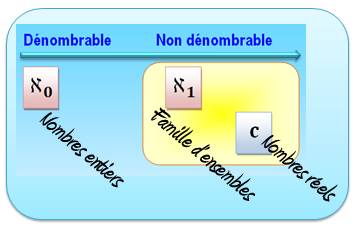
Deux infinis Les nombres entiers La suite des nombres entiers se prolonge autant que l'on veut sans jamais finir. On dit qu'ils sont en quantité infinie. Les nombres pairs, les impairs, les premiers ou encore les fractions sont tous en quantité infinie. On montre qu'il s'agit du même type d'infini, noté (aleph 0). Famille de nombres Si on prend les nombres un par un, deux par deux … ou même n'importe comment, on forme une famille d'ensembles de nombres. F = {{0}, {1}, {10,52}, (17, 1000, 12345} …} Georg Cantor a démontré que tous ces ensembles sont plus nombreux que les nombres entiers eux-mêmes. On note cet infini: . Premier paradoxe L'infini c'est l'infini, non? Ce fut bien embarrassant d'admettre qu'il y avait plusieurs niveaux d'infinis. On les appelé des transfinis. Le premier infini est dit dénombrable. Le deuxième est non-dénombrable, et il est le plus petit de ce type. Dit autrement, aucune quantité infinie ne viendra se mettre au milieu.		Troisième infini Les nombres réels Les nombres entiers avec les fractions forment l'ensemble des nombres rationnels. Avec, en plus, les nombres irrationnels (comme les racines des nombres) ou les transcendants (comme ), on a les nombre réels Les nombres réels sont très, très nombreux! à tel point que leur quantité est un infini plus grand que celui des nombres entiers. Il est noté c. Où se situe ce nouvel infini? On sait qu'il est plus grand ou égal à celui des familles de nombres. Second paradoxe Les mathématiciens pensent que les deux infinis sont les mêmes. Ils font ce qu'il est convenu d'appeler l'hypothèse du continu. Gödel et Chen ont démontré qu'on ne saura jamais si cette hypothèse est vraie ou fausse.
Pour en savoir plus	>>> Infini >>> Transfinis >>> Grands nombres (gogol et plus) >>> Georg Cantor		>>> Aleph >>> Compter les ensembles >>> Hypothèse du continu

102. Nombres triangulaires
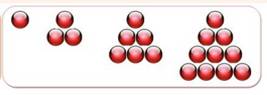
Origine On connait les nombres carrés (4^2 = 16), on connait les nombres cubes (4^3 = 64), mais les nombres triangulaires ? Dans l'Antiquité, les savants essayaient de trouver une signification aux nombres en les organisant en figures géométriques. Nombres triangulaires Les nombres sont symbolisés par des billes. On forme les nombres triangulaires en superposant les plus petits nombres sur les plus grands. Le troisième nombre triangulaire est égal à 3 + 2 + 1 = 6. Pour obtenir le suivant, on ajoute 4: 6 + 4 = 10. Question Quel est le plus petit nombre triangulaire et carré? 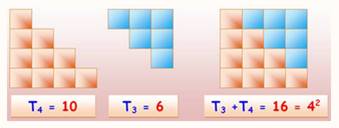C'est 36 = 6^2 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8		Somme des nombres de 1 à n Le énième nombre trianglaire est égal à la somme de tous les nombres de 1 à n. On montre que cette somme vaut Tn = ½ n (n + 1) Ainsi le dixième nombre triangulaire est T10 = ½ (10 x 11) = 55 Triangulaires et carrés Deux triangulaires voisins s'associent pour faire un carré. Trois triangulaires Il suffit de faire la somme de trois triangulaires (au plus) pour obtenir tous les nombres entiers. Démontré en 1796 (Gauss)
Brèves liées	>>> Nombres triangulaires – Calcul de la formule
Pour en savoir plus	>>> Nombres triangulaires >>> Décade de Pythagore		>>> Nombres géométriques >>> Somme des entiers

103. Carré et deux triangles
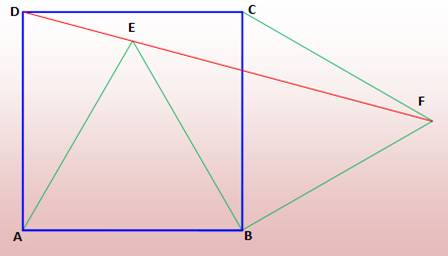
Un carré ABCD et deux triangles équilatéraux AEB et BFC. Montrez que les points D, E et F sont alignés. (DEF – en rouge – est une droite). Il existe de nombreuses démonstrations: Comparaison des angles autour de E (démonstrations simples); Calcul avec les coordonnées des points; Emploi des relations d'Al Kashi; Constat de symétrie avec duplication de la figure et rotation; etc.
Pour en savoir plus	>>> Triangles équilatéraux et carré

104. Algo. d’Euclide – Calcul du PGCD
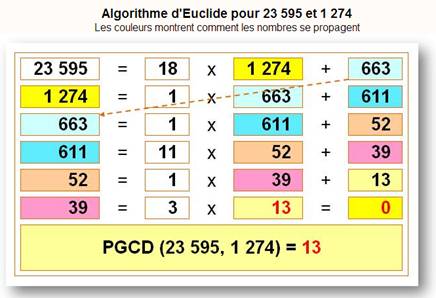
PGCD Plus grand commun diviseur: le nombre le plus grand qui divise à la fois plusieurs nombres Algorithme d'Euclide Méthode systématique pour la recherche d’un facteur commun à deux nombres quelconques. Sur la première ligne, on cherche combien de fois le plus petit nombre est contenu dans le plus grand. C’est la division euclidienne. On recommence sur la ligne suivante avec les valeurs trouvées sur la première ligne. Le procédé est utilisé jusqu’à un reste nul ou alors un facteur unité, auquel cas les deux nombres sont premiers entre eux.		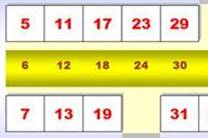Méthode pratique Observez la propagation des nombres en oblique vers la gauche. 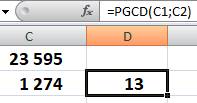Tableur Un tableur fournit directement le PGCD de plusieurs nombres =>
Brèves liées	>>> Identité de Bachet-Bézout – B161
Pour en savoir plus	>>> Diviseurs >>> PGCD >>> Algorithme d’Euclide		>>> Euclide (vers 300 av. J.-C.) >>> Division euclidienne >>> Identité de Bachet-Bézout

105. Carl Friedrich GAUSS (1777-1855 )
Le prince des mathématiques Sa devise: Pauca sed matura: peu de choses, mais des choses mûres.		Né à Brunswick en Allemagne. À huit ans, il calcule rapidement la somme de mille entiers successifs en inventant lui-même la méthode. À dix-huit ans, il démontre l’impossibilité de construire l’heptagone régulier avec règle et compas. Pour sa thèse, il démontre le théorème fondamental de l’algèbre donnant la quantité de solutions possibles des équations algébriques: la quantité de racines, réelles et complexes, d'un polynôme est égale à son degré. Gauss sera titulaire de la chaire de mathématiques de l’université de Göttingen. Il est, également astronome, est aussi le directeur de l’observatoire de cette même université. En physique son nom reste attaché à l’unité d’intensité du champ magnétique (le gauss, remplacé par le tesla) et à un théorème fondamental de l’électrostatique. En statistique, on connait la courbe de Gauss et ses lois de distribution de probabilités. En théorie des nombre, il écrit : Disquisitiones arithmeticae. Nous sommes en 1801 et il a 24 ans. Dans ce livre, il introduit l’arithmétique modulaire. La suite donne la solution à de nombreux problèmes jusqu’alors non résolus. Parfois, il apporte même plusieurs démonstrations.
Pour en savoir plus	>>> Gauss >>> Gauss – Somme des entiers >>> Théorème fondamental de l'algèbre >>> Arithmétique modulaire		>>> Théorème de Gauss sur la constructibilité >>> Heptagone >>> Courbe de Gauss

106. Somme des deux âges
Énigme Gilbert et son fils Théo. Ajoutez les deux âges puis les deux années de leur naissance. Vous prétendez connaitre le total. Si nous sommes en 2016, ce sera 4 032.		Réponse En effet, disons que Gilbert a 40 ans; il est né en (2016 – 40); Théo à 10 ans; il est né en (2016 – 10). L'opération demandée est la suivante: 40 + 10 + (2016 – 40) + (2016 – 10) = 2 x 2016 = 4 032. Commentaire Il est évident que l'âge d'une personne ajouté à son année de naissance donne l'année en cours. Avec deux personnes, deux fois l'année en cours. On aurait pu en mettre trois ou quatre … pour tromper son public.
Pour en savoir plus	>>> Âge deviné		>>> Énigmes classiques >>> Jeux et énigmes

107. Nombres PARFAITS
Définition Un nombre est parfait s'il est égal à la somme de ses diviseurs propres Quantité On ne connait que 49 nombres parfaits en 2016, mais on conjecture qu'ils sont une infinité. Ils sont tous pairs et on ne connait pas encore de nombres parfaits impairs Liste des plus petits nombres parfaits 6, 28, 496, 8 128, 33 550 336 … Particularités des nombres parfaits pairs Ils se terminent tous par 6 ou 28. Ils sont tous triangulaires. Ils sont somme des cubes des nombres impairs consécutifs, sauf 6: 28 = 1^3 + 3^3.			Exemples 6 = 2 x 3 Diviseurs propres: 1, 2, 3 Somme: 1 + 2 + 3 = 6 28 = 2 x 2 x 7 Diviseurs pourpres: 1, 2, 4, 7, 14 Somme: 1 + 2 + 4 + 7 + 14 = 28 Forme 6 = 2^1 x (2^2 – 1) 28 = 2^2 x (2^3 – 1) P = 2^k-1 x (2^k – 1) Tous les nombres parfaits pairs sont de cette forme avec 2^k – 1, un nombre de Mersenne premier.
Brèves liées	>>> Diviseurs >>> Nombres triangulaires	>>> Nombres 6 et 28 – Parfaits
Pour en savoir plus	>>> Nombres parfaits >>> Nombres de Mersenne	Nombre 6 Nombre 28

108. Nombre 6 – SIX
Propriétés Le nombre 6 est pair. Il est composé: 6 = 2 x 3 Il est triangle et factorielle: 1 x 2 x 3 = 1 + 2 + 3 = 6. Le produit de deux nombres se terminant par 6 se termine par 6: 16 x 26 = 416 Son carré est égal à la somme des trois premiers nombres au cube: 6² = 1^3 + 2^3 + 3^3 = 1 + 8 + 27 = 36 Nombre parfait Le nombre 6 est divisible par 1, 2 et 3 et la somme de ces trois nombres est égale justement à 6. Voisin des nombres premiers Tous les nombres premiers à partir de 6 sont voisins d'un multiple de 6. Ex: 11 et 13 sont voisins de 12.		Biologie Tous les insectes ont six pattes (hexapode). Les araignées en ont huit. Chimie L'atome de carbone le plus abondant possède 6 électrons, 6 protons et 6 neutrons. Un élément fondamental de la vie avec l'hydrogène, l'oxygène et l'azote. Découvert comme élément chimique en 1789 par Lavoisier.
Brèves liées	>>> Nombre 5 >>> Nombre 7 >>> Nombres triangulaires		>>> Nombres parfaits >>> Nombres premiers
Pour en savoir plus	>>> Nombre 6– Culture >>> Nombre 6 – Maths >>> Barre magique des premiers		>>> Factorielles >>> Nombres triangulaires >>> Carbone >>> Insectes

109. Multiplication de nombres entiers
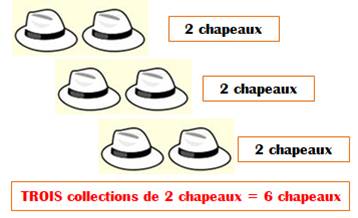
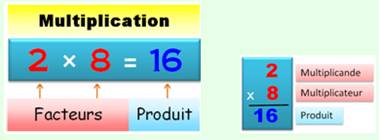
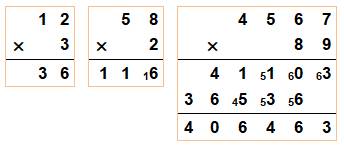
Principe La multiplication consiste à rapprocher plusieurs collections comportant la même quantité d'objets et à compter les objets de la nouvelle collection. Trois fois 2 = 2 + 2 + 2 = 6 Multiplication Application: calcul des aires L'aire d'un rectangle est obtenue en multipliant la longueur par la largeur (les puristes diront: la mesure de la longueur par la mesure de la largeur).		Multiplication posée On effectue successivement: 3x2 = 6 puis 3x1 = 3, en partant toujours des chiffres de droite. Si le résultat présente une dizaine, on la note en petit (ou on la retient mentalement). Avec un multiplicateur à plusieurs chiffres, on forme des étages en décalant chacun d'un cran vers la gauche, puis on additionne le tout. Multiplication en ligne 2 x 58 = 58 x 2 = 116 On peut échanger les facteurs. 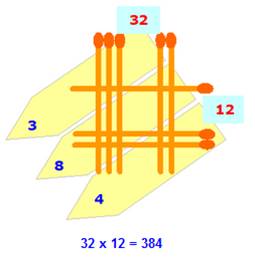La multiplication est commutative. Multiplication amusante
Brèves associées	>>> Addition >>> Soustraction		>>> Moins par moins = plus >>> Tables de multiplication
Pour en savoir plus	>>> Multiplication >>> Multiplication avec allumettes, égyptienne, musulmane …		>>> Opérations – Index >>> Aire du rectangle

110. Moins par moins = PLUS
Règle des signes dans un produit Analogie J'ai (+) une dette (-), c'est de l'argent négatif (-). On me retire (-) ma dette (-), c'est du positif (+) pour moi		Poème d'Hervé Bazin (1911−1996)
Brèves associées	>>> Multiplication
Pour en savoir plus	>>> Moins par moins		>>> Bases de l'algèbre

111. Multiplication et parenthèses
Priorité de la multiplication Par convention, la multiplication est prioritaire sur l'addition et la soustraction. 1 + 2 x 3 = 1 + 6 = 7 (et non: 3 x 3 = 9). Pour éviter toute ambiguïté, on peut placer des parenthèses: 1 + (2 x 3) = 7 ou alors (1 + 2) x 3 = 3 x 3 = 9 Autre exemple: 20 – (2 x 3) = 20 – 2 x 3 = 20 – 6 = 14 Curiosités 1 + 2 x 3 x 4 = 1 + 24 = 25 = 5² L'opération et son résultat utilisent les cinq premiers nombres. 1 + (2 + 3 + 4) x (5 + 6) = 100 Le nombre cent obtenu avec une opération impliquant les six premiers nombres dans l'ordre.		Opérations composites (exemples)
Brèves associées	>>> Multiplication >>> Opérations et parenthèses		>>> Règle des signes
Pour en savoir plus	>>> Bases de l'algèbre		>>> Obtenir 100 avec les chiffres de 1à 9

112. Théorème de Thalès
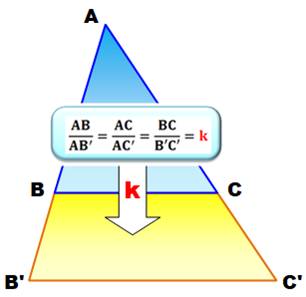
Ce que dit le théorème en bref Dans un effet de loupe les proportions sont conservées. Toutes les dimensions sont augmentées dans le même rapport, le rapport de grossissement k. En géométrie des triangles Sur la figure de droite, on observe que les angles des triangles ABC et AB'C' sont égaux deux à deux. On dit que les triangles sont semblables ou mieux, homothétiques. Les mêmes proportions sont observées même si ces deux triangles sont séparés.		Théorème de Thalès Les droites portant BC et B'C' sont parallèles. Si ces proportions sont observées, alors les droites portant BC et B'C' son parallèles. Exemple AB = 6, AC = 8 et BC = 10 Avec k = 1,5 AB' = 9, AC' = 12 et BC' = 15
Brèves associées	>>> Théorème de Pythagore
Pour en savoir plus	>>> Théorème de Thalès >>> Thalès (de – 625 à – 547)		>>> Triangles semblables >>> Homothétie

113. Premiers jumeaux
Sandwiche en multiple de 6 Nous savons que les nombres premiers sont tous voisins d'un multiple de 6, à un près. Ils de la forme 6k – 1 ou 6k + 1. Lorsque le multiple de 6 est accompagné de deux nombres premiers, on dit qu'ils sont jumeaux. L'écart entre les deux valeurs est égal à 2. Au départ … Seuls les deux plus petits nombres premiers (2 et 3) se suivent. Ensuite, la distance minimale entre deux nombres premiers est 2. Le nombre intermédiaire est non seulement pair, mais divisible par 6. La somme de deux premiers jumeaux est divisible par 12. En effet: (6k – 1) + (6k + 1) = 12k. Conjecture des nombres jumeaux On conjecture (on parie) que la quantité des premiers jumeaux est infinie. Mais personne n'a réussi à le démontrer. En 1912, le mathématicien Landau a mis cette démonstration dans le top 4 des problèmes les plus durs à résoudre sur les nombres premiers.		Les plus petits nombres jumeaux autour d'un multiple de 6 Couple de nombres premiers jumeaux jusqu'à 100 (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73) … Autre conjecture Sauf pour un nombre fini d'exceptions, les nombres pairs sont la somme de deux nombres parmi les premiers jumeaux. Somme des inverses La somme des inverses des nombres premiers converge vers 1,902, le nombre de Brun: 1/3 + 1/5 + 1/5 + 1/7 + 1/11 + … 1,902
Brèves associées	>>> Nombres premiers >>> Premiers en 6k+1 et 6k+5		>>> Nombres pairs et impairs
Pour en savoir plus	>>> Premiers jumeaux >>> Nombre de Brun		>>> Les quatre problèmes de Landau >>> Conjectures

114. Les échecs
Jeu classique d'échecs La légende de sa création Le roi indien Shirham accorde une récompense au grand vizir pour avoir inventé le jeu d'échec. Celui-ci demande un grain de blé sur la première case et le double sur les cases suivantes, jusqu'à la 64^e. La quantité est astronomique! Le roi avisé lui accorde à condition qu'il compte lui-même les grains. Le jouer d'échecs – Edgar Poe Edgar Poe a écrit le joueur d’échecs de Maelzel en 1836: histoire d'un automate joueur d’échecs, dans laquelle, en fait, un nain y est caché. La machine de Babbage (1834) existait déjà. Mais, Edgar Poe pense qu'il est plus difficile de concevoir une machine qui sait jouer aux échecs qu'une machine qui calcule. Il rêve: "si elle existait, ce serait la plus extraordinaire invention de l’humanité".		Quantité de parties Il est totalement illusoire d'analyser toutes les parties possibles aux échecs. Il y en a plus de 10^120 (un 1 suivi de 120 zéros). Il faudrait faire fonctionner tous les ordinateurs actuels pendant des milliards d'années pour faire le tour de toutes les parties. Historique En 1967, les programmes sur ordinateurs atteignent un bon niveau de jeu. En 1997, l'ordinateur Deeper Blue d'IBM bat le champion du monde Garry Kasparov. En 2017, les machines à apprentissage profond, type AlphaGo, surpassent tout joueur humain. Machines du type Deeper Blue Bien sûr, il existe une analyse des coups à partir des règles du jeu. L'ordinateur calcule même une note d'efficacité des coups. Mais, la clé de la réussite: une bibliothèque d'ouvertures basée sur un grand nombre de parties jouées dans le passé. Machines du type AlphaGo Seules sont implémentées les règles du jeu, et c'est l'apprentissage profond et les ajustements automatiques des réseaux neuronaux qui font le reste. Le programme devient opérationnel après un apprentissage durant lequel la machine se forge sa logique propre.
Brèves associées	>>> Puissance de 2 et échiquier
Pour en savoir plus	>>> Échecs – Jeu >>> Échecs – Ordinateurs >>> Échecs – Légende		>>> Babbage et son calculateur >>> Apprentissage profond

115. Dessin du carré avec Scratch
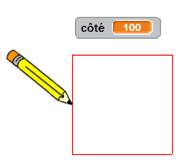
But Dessiner un carré centré dont on précise la longueur du côté. Programme ultrasimple pour s'initier. Rappel: le téléchargement de ce logiciel est gratuit. Préparation Choisir un nouveau lutin pour remplacer le chat par un crayon (facultatif). Créer une variable nommée "côté". Accès en cliquant sur "données". Initialisation du dessin On demande d'effacer tout au démarrage, lorsqu'on clique sur le drapeau vert. Le crayon est placé en position centrale (x = 0 et y = 0), stylo levé pour ne rien écrire. On demande de spécifier la longueur du côté. Une boite de dialogue s'ouvre en bas de l'écran. Indiquez une valeur avec le clavier numérique et faites "entrée". On place cette valeur (réponse) dans la variable "côté".
Position de départ du tracé Le crayon est envoyé au milieu gauche du carré (x = côté/2). On se prépare à dessiner le carré en rouge. Dessin du carré Suite d'instructions simples demandant à avancer vers le haut d'une longueur égale à côté/2 Puis vers la droite d'une longueur égale à côté. Etc. Pour finir par fermer le carré avec une progression vers le haut d'une longueur égale à côté/2. Les temporisations d'un dixième de seconde servent à laisser le temps d'observer le mouvement du crayon qui, sinon, est instantané.
Brèves associées	>>> Mon premier programme Scratch
Pour en savoir plus	>>> Programmation – Débutant >>> Programmation – Index	>>> Programmation avec Scratch

116. Triangle isocèle
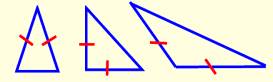
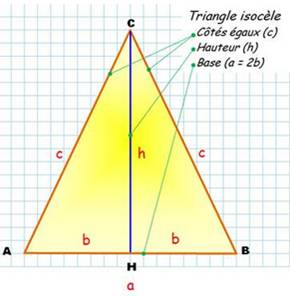
Types de triangle isocèle Le triangle isocèle a deux côtés de même longueur. Il a aussi deux angles égaux. Le troisième angle, dit au sommet, peut être aigu, droit ou obtus. Le côté opposé à l'angle au sommet est la base du triangle isocèle. Avec un angle droit, le triangle est isocèle rectangle. Avec un angle au sommet égal à 60°, le triangle est équilatéral Avec un angle au sommet de 36°, c'est un triangle isocèle d'or. Hauteur CH La droite CH est à la fois hauteur du triangle ABC médiane du triangle ABC médiatrice de AB bissectrice de l'angle au sommet axe de symétrie Caractéristiques Périmètre: P = a + 2c Aire: A = ½ a . h = ½ c² . sin C Angle à la base:			Théorème des médianes Dans un triangle isocèle les médianes issues de A et B sont de même longueur. Réciproquement, si deux médianes sont de même longueur, le triangle est isocèle.
Brèves associées	>>> Triangles	>>> Triangle rectangle
Pour en savoir plus	>>> Triangle isocèle >>> Triangles isocèles d'or	>>> Angles – Types

117. Pépites numériques
Cinq nombres en suivant Sommes avec les six premiers nombres impairs Dix et cent avec les quatre premiers nombres Carré et cube avec 3, 4, 5 et 6		Multiplication des uns Tout en huit
Brèves associées	>>> Nombres pannumériques		>>> Nombres uniformes
Pour en savoir plus	>>> Pépites numériques		>>> Nombres de Demlo

118. Alphabet grec
Lettres grecques utilisée en math et en physique: en jaune cerclé
Pour en savoir plus	>>> Alphabet grec	>>> Langues – Index

119. Chapeaux – Énigme
Devinette Trois personnes sortent du restaurant un peu éméchés. Ils reprennent leur chapeau au hasard. Quelle est la probabilité que deux seulement aient pris leur chapeau ?		Réponse Probabilité nulle car, si deux personnes portent leur propre chapeau, le troisième aussi.
Brèves associées	>>> Énigme des lapins et des canards >>> Énigme des trois filles
Pour en savoir plus	>>> Énigmes de chapeaux >>> Énigmes des chaussettes		>>> Énigmes classiques >>> Jeux et énigmes

Retour	Brèves de maths – Page 5
Suite	Brèves de maths – Page 7
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve06.htm