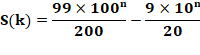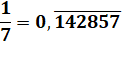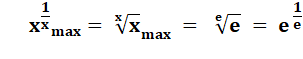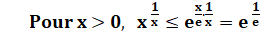NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 40 (780-799)		Page 41 (800-819)		Page 42 (820-839)		Page 43 (840-859)		Page 44 (860-879)
	Page 45 (880-899)		Page 46 (900-919)		Page 47 (920-939)		Page 48 (940-959)		Page 49 (960-979)

BRÈVES de MATHS – Page 41

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

800. Somme des nombres à k chiffres
Somme avec un ou deux chiffres S(1) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 S(2) = 100 + 101 + … + 999 = 4 905 La somme des nombres à deux chiffres est égale à 4 905. C'est la somme de tous les nombres jusqu'à 999, diminuée de la somme de ceux jusqu'à 99. Formules de calcul Allure des nombres pour k > 2 S(k) = 494 99…9_k-3 55 00…0_k-2		Table des sommes des nombres à k chiffres (k, S)
Brèves associées	>>> Somme des carrés des entiers	>>> Brèves Calculs – Index
Pour en savoir plus	>>> Somme des nombres à k chiffres	>>> Calcul de sommes – Index

801. Construire 1 connaissant 2
Problème On dispose d'une règle avec deux marques espacées d'une distance disons de 2 unités. Construire un segment de longueur unité avec cette seule règle. Solution Tracer deux droites sécantes (bleues). Porter deux fois de suite la longueur 2 sur chacune (ici symbolisée par des cercles). Tracer les deux segments (verts) joignant les marques. Porter la longueur 2 sur le plus grand segment et joindre cette marque au sommet du triangle (rose). L'intersection sur le petit segment définit un segment de longueur unité.		Figure Explication Les triangles verts sont dans une homothétie de rapport 1/2. Les segments verts sont dans le même rapport.
Brèves associées	>>> Carré passant par quatre points		>>> Brèves Construction – Index
Pour en savoir plus	>>> Construction de 1 en connaissant 2		>>> Constructions des nombres

802. Transformation Powertrain
Procédé Création d'un nouveau nombre à partir des chiffres d'un nombre: c'est le produit de chaque chiffre de rang impair élevé à la puissance du chiffre de rang pair. Exemple		Trajectoire Le procédé est répété sur les images obtenues et il est arrêté sur un point fixe ou la création d'une boucle. Exemple de trajectoire avec le nombre 55 55, 3125, 96, 531441, 500, 0 Le nombre 2 592 est le seul dont l'image est lui-même.
Brèves associées	>>> Cycle de Collatz généralisé		>>> Brèves Itérations – Index
Pour en savoir plus	>>> Transformation Powertrain		*>>> Nombre 2 592 dit faute de frappe.*

803. Super-Harshad
Un nombre de Harshad est divisible par la somme de ses chiffres. Un nombre super-Harshad reste Harshad avec ses puissances successives.		Le nombre 6 est Harshad jusqu'à la puissance 10.
Brèves associées	>>> Nombres de Harshad >>> Nombres de Harshad et 200		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres super-Harshad		>>> Nombres de Harshad

804. Premiers avec équi-éloignés
On cherche les nombres comme 4 qui sont le rang k d'un nombre premier tel qu'à la distance k de part et d'autres du nombre premier P_k on retrouve deux nombres premiers. P_k – k = Premier P_k + k = Premier		Exemple avec k = 4 Exemple avec k = 2022
Brèves associées	>>> Premiers équilibrés		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Premiers équi-éloignés >>> Nombre et année 2022		>>> Types de premiers – Index

805. Pannumériques divisibles par 11
Exemple 123495768 est divisible par 11. En fait: la somme des cinq chiffres de rang impair (1, 3, 9, 7 et 8) est 28, et celle des quatre chiffres de rang pair (2, 4, 5, 6) est 17. La différence 28 – 17 = 11 indique que ce nombre est divisible par 11. Quantité Le tableau montre les 11 possibilités de somme 17 et 28. Pour chaque ensemble des quatre nombres, il y a 4! = 24 permutations et pour ceux à cinq nombres il y en a 5! = 120. Bilan: 11 x 24 x 120 = 31 680 pannumériques divisibles par 11.
Brèves associées	>>> Divisibilité par 11 – Dominos	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Pannumériques divisibles par 11	>>> Divisibilité par 11

806. Comparez 99! et 50⁹⁹
Face à ces grands nombres, la comparaison ne semble pas facile sans avoir recours à une calculette. Pourtant, un peu d'astuce permet de montrer que 50⁹⁹ est bien plus grand que 99! La démonstration passe par cette écriture développée en constatant que le 50 est au milieu en haut comme en bas, ce qui offre une symétrie à exploiter:		Valeurs numériques et rapport entre elles Une propriété bien utile
Brèves associées	>>> Équation avec racines cubiques		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Comparaison – Solution		>>> Algèbre – Index

807. Carrés et factorielles
Différence de factorielles successives La différence entre deux factorielles successives est égale: au produit de la plus petite par ce nombre sans factorielle, et au carré de la plus petite multiplié par la factorielle du nombre inférieur. 3! – 2! = 2 × 2! = 2² × 1! 4! – 3! = 3 × 3! = 3² × 2! … 11! – 10! = 10 × 10! = 10² × 9! 12! – 11! = 11 × 11! = 11² × 10!		Carré et trois factorielles successives
Brèves associées	>>> Carré = Somme de cubes		>>> Brèves Identités – Index
Pour en savoir plus	>>> Carrés et factorielles		>>> Factorielles

808. Racine numérique des carrés
Théorème La racine numérique des carrés est toujours 1, 4, 7 ou 9. Si la racine numérique n'est pas l'un de ces chiffres, le nombre n'est pas un carré.				Exemples 4² = 16 et RN = 1 + 6 = 7 5² = 25 et RN = 2 + 5 = 7 6² = 36 et RN = 3 + 6 = 9
Programme Maple		Commentaire RN est une procédure, une fonction qui retourne la racine numérique de n. Le nombre n est converti en sa suite de chiffres, lesquels sont additionnés en s. Si cette somme s est à deux chiffres, elle est réinjectée dans la procédure RN (principe du calcul récursif). La valeur finale de s est retournée vers le programme d'appel. Le programme principal compose un ensemble – présence des accolades { } – des diverses valeurs prises par la racine numérique des carrés. Le point virgule final implique une impression.
Brèves associées	>>> Factorielle		>>> Brèves Programmes – Index
Pour en savoir plus	>>> Racine numérique des puissances >>> Racine numérique – Propriétés		>>> Programmation >>> Récursivité

809. Nombre 24 en trois chiffres
Un jeu classique consiste à atteindre un nombre donné en utilisant les opérations ordinaires et des chiffres imposés. Cet exemple montre comment atteindre le nombre 24 avec trois fois le même chiffre. On profite du fait que: 24 = 4x3x2x1 = 4! On utilise l'astuce: .1 surligné = 0,111… Alors 0,111… = 1 / 9 avec 9 le carré de 3. Un exemple célèbre demande d'atteindre tous les nombres successivement en utilisant quatre fois le chiffre 4.
Brèves associées	>>> Nombre et ses chiffres	>>> Brèves Jeux – Index
Pour en savoir plus	>>> Nombre 4 >>> Nombre 24	>>> Jeu du quatre 4 >>> Jeux avec les chiffres – Index

810. Points de Lagrange
Forces de gravitation La loi de la gravitation indique que deux objets ayant une masse s'attirent mutuellement. Nous-mêmes sommes attirés vers le centre de la Terre. Prenons un objet (un satellite artificiel) placé entre le Soleil et la Terre. L'attraction de l'un et l'attraction de l'autre se combinent. Il existe un point sur l'axe Soleil-Terre où ces forces sont égales. C'est le premier point de Lagrange (L₁). Les cinq points de Lagrange Une étude approfondie des lois de l'attraction, menée en premier par Joseph Lagrange (1736-1813), a conduit à identifier cinq points d'équilibre: trois sont situés sur l'axe entre les deux objets et deux à un angle de 60° de l'axe et sur l'orbite de la Terre. Ces cinq point existent pour tout astre qui orbite autour d'un autre.
Mouvement Notez que l'ensemble Terre et points de Lagrange orbitent autour du Soleil. Le centre de gravité Soleil-Terre étant légèrement à l'écart du centre du Soleil, lui aussi sera animé d'un mouvement de rotation.		Télescope James Webb En fin 2021, le successeur de Hubble sera placé au point de Lagrange L₂ situé à 1,5 million de km de la Terre. En position d'équilibre instable, un minimum d'énergie suffira à le recaler: réservoir d'ergol pour une autonomie de 10 ans.
Brèves associées	>>> Galileo & GPS	>>> Brèves Sciences – Index
Pour en savoir plus	>>> Points de Lagrange >>> Gravitation	>>> Télescope James Webb >>> Centre de Gravite Soleil-Terre – Animation

811. Oméga 3 et oméga 6
Oméga 3 désigne des acides gras qui possèdent une double liaison au niveau du troisième atome de carbone en partant de la fin de la chaine. Idem avec oméga 6, pour le sixième carbone. Les acides gras sont des molécules à longue chaines d'atomes de carbone avec une liaison simple (acides gras saturés) ou double (acides gras saturés en hydrogène). Parmi les insaturés, il des molécules à liaison double droites (dits "trans") ou à liaison coudées (dits("cis"). Les "trans" sont d'origine animale et sont plutôt à bannir (objectif OMS pour 2023). Les "cis" sont essentiels à la santé, comme les oméga 3 et les oméga 6 que l'on trouve dans les huiles végétales et les poissons gras.
Brèves associées	>>> Quantité de sable dans l'Univers	>>> Brèves Sciences – Index
Pour en savoir plus	>>> Diététique	>>> Biologie – Index

812. Repunits et premiers
Théorème Tout nombre premier supérieur à 5 divise un repunit formé de p – 1 fois le chiffre"1". Le nombre premier 7 divise le repunit 111 111, de longueur 6. Le quotient 15 873 multiplié par 9 donne la période de la fraction 1/7		Exemples
Brèves associées	>>> Divisibilité de Aⁿ – Bⁿ		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Repunits et premiers		>>> Repdigits et repunits

813. Multiplication magique
Le tour Sorte de tour de magie ou de calcul mental éclair. Une personne inscrit un nombre de trois chiffres sur le tableau. Je le répète. Il en choisit un second. Je forme son complément à 9, sans le dire, bien sûr ! Je prétends calculer instantanément la somme des produits de ces nombres. Le calcul Je retire 1 au premier nombre (566) et j'en prends le complément à 9 (433). C'est fini !
Brèves associées	>>> Multiplication magique par 91	>>> Brèves Magie – Index
Pour en savoir plus	>>> Multiplication magique	>>> Magie – Index

814. Division mystérieuse
Le mystère Un internaute me sollicite pour comprendre le mystère de 1/168 qui "attire" les décimales répétitives de 1/7 = 0, 142857 … ou ses permutations circulaires. Explication du mystère Il se trouve que toutes les fractions en 1/7, y compris les fractions en 1 sur multiple de 7, produisent un développement décimal avec ces chiffres répétitifs. Or, en l'occurrence, le nombre proposé est un multiple de 7. En effet: 168 = 2³ x 3 x 7. Pas étonnant d'y retrouver les chiffres répétitifs de 1/7. Dans le tableau du bas, des "0" ont été ajoutés pour obtenir une constante entière.
Brèves associées	>>> Division par 7 – Nombre 142 857	>>> Brèves Opérations – Index
Pour en savoir plus	>>> Nombre 142857 >>> Nombre 168	>>> Nombres périodiques

815. Problème de Steiner: x^1/x
Problème de Steiner Ce problème a été formulé et résolu par Jakob Steiner en 1850: quelle est la valeur qui maximalise la valeur de la racine énième de x ? Démonstration Sur le graphe présenté: Le"vert" est en dessous de "rouge": En élevant à la puissance 1/x:
Brèves associées	>>> Volume maximal de la boite	>>> Brèves Analyse – Index
Pour en savoir plus	>>> Problème de Steiner	>>> Racine

816. Rang des Fibonacci

Sur ce tableau quatre nombres (0, 1, 5 et 10) sont des nombres de Fibonacci dont la racine numérique (Rn) est égale au rang du nombre de Fibonacci (R).

Le plus petit non trivial

F₁₀ = 55 et Rn(F₁₀) = 5 + 5 = 10

On pense qu'il n'existe que 20 tels nombres avec les rangs

0, 1, 5, 10, 31, 35, 62, 72, 175, 180, 216, 251, 252, 360, 494, 504, 540, 946, 1188, 2222.

Le plus grand connu

F₂₂₂₂ = 10496 …9561 Il compte 465 chiffres.

R	F_R	Rn
0	0	0
1	1	1
2	1	1
3	2	2
4	3	3
5	5	5
6	8	8
7	13	4
8	21	3
9	34	7
10	55	10
11	89	17

Brèves associées

>>> Mot de Fibonacci et sa fractale

>>> Brèves Itérations – Index

Pour en savoir plus

>>> Fibonacci et racine numérique

>>> Nombres de Fibonacci

>>> Racine numérique

817. Marguerite magique des nombres premiers
Propriété Les multiples de 6 sont inscrits sur la barre centrale jaune. Tous les nombres premiers, à partir de 5, sont situés sur la barre du haut ou du bas (rouge) Dit autrement: un nombre premier, outre 2, 3 et 5, est toujours de la forme 6k – 1 ou 6k + 1. En gris, les exceptions.		Un truc pour retrouver les nombres premiers jusqu'à 100 Agrandir l'image
Brèves associées	>>> Algorithme de recherche		>>> Brèves Premiers – Index
Pour en savoir plus	>>> Barre magique des premiers		>>> Nombres premiers

818. Marguerite magique des nombres premiers
Propriété Les nombres successifs sont inscrits sur cette roue à 30 rayons ou marguerite à 30 pétales. Sur cette marguerite, seuls huit pétales sont susceptibles de contenir des nombres premiers (à partir de 7). Ils sont tous voisins de pétales contenant des multiples de 6. Intérêt Cette propriété est exploitée pour réaliser le crible de la roue (wheel sieve). Seuls les nombres dans ces pétales sont à examiner pour identifier les nombres premiers.		Agrandir l'image
Brèves associées	>>> Nombre premier – Trouvez-le		>>> Brèves Premiers – Index
Pour en savoir plus	>>> Crible de la roue		>>> Nombres premiers

819. Les crayons emmêlés
Énigme Le journal Ouest-France propose cette énigme: combien de crayons sur cette image: 9, 10, 11 ou 12 ? Le journal commente: mais croyez-nous lorsque nous vous disons que 75% des gens n’ont pas donné la bonne réponse lors de leur première tentative. Indice Ne comptez pas les crayons, vos yeux vont se brouiller. Mais, comptez les mines. Réponse >>>
Brèves associées	>>> Crayons côte à côte – Angle ?	>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Un seul trait de crayon	>>> Énigmes et jeux – Index

Retour	Brèves de maths – Page 40
Suite	Brèves de maths – Page 42
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve41.htm

Il y a 6 + 5 = 11 crayons

>>>

800. Somme des nombres à k chiffres

801. Construire 1 connaissant 2

802. Transformation Powertrain

803. Super-Harshad

804. Premiers avec équi-éloignés

805. Pannumériques divisibles par 11

806. Comparez 99! et 5099

807. Carrés et factorielles

808. Racine numérique des carrés

809. Nombre 24 en trois chiffres

810. Points de Lagrange

811. Oméga 3 et oméga 6

812. Repunits et premiers

813. Multiplication magique

814. Division mystérieuse

815. Problème de Steiner: x1/x

816. Rang des Fibonacci

817. Marguerite magique

des nombres premiers

818. Marguerite magique

des nombres premiers

819. Les crayons emmêlés

806. Comparez 99! et 50⁹⁹

815. Problème de Steiner: x^1/x