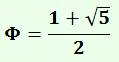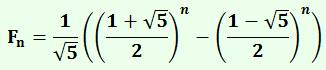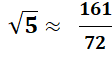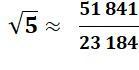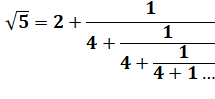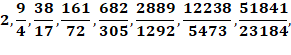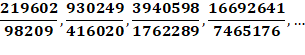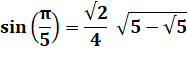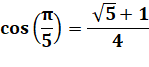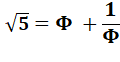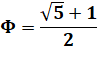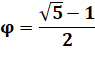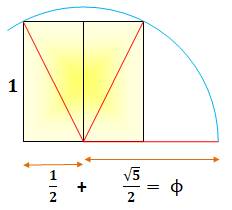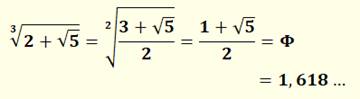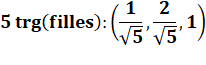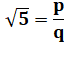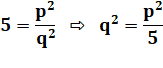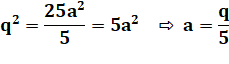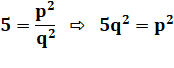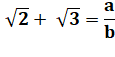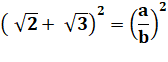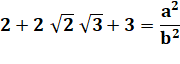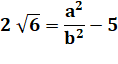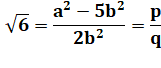|
Édition du: 12/01/2022 |
|
INDEX |
RACINES
CARRÉES |
|||
![]()
|
RACINE CARRÉE de 5
Valeur précise à 99,99% Nombre algébrique
, irrationnel |
||
|
|
Sommaire de cette page >>> Valeur de Racine de 5 >>> Fraction continue >>> Trigonométrie >>> Nombre d'or >>> Fraction continue >>> Géométrie >>> Racine de 5, irrationnelle >>> Racine de 2 plus racine de 3, irrationnelle |
Débutants Glossaire |
En bref
|
Ce nombre est une composante du nombre d'or. |
Ce nombre est une composante de la formule de Binet donnant les nombres de Fibonacci. |
|
|
|
|
Note: le symbole radical
implique que la racine positive. Si on veut aussi la racine négative, on écrit: x² = 5 à pour racines: |
=
2, 2360679774 9978969640 9173668731 2762354406 1835961152 5724270897
2454105209 2563780489 9414414408 3787822750 … On connait plus de 2
000 milliards de décimales. |
|
|
Binaire Hexadécimal |
10,0011110001101110... 2,3C6EF372FE94F82C... |
|
|
|
à
10-4 près. |
|
|
|
à
0,41 10-9 près. Voir Calcul de Brahmagupta |
|
|
|
=
0, 4472135954 9995793928 1834733746
2552470881 2367192230 … |
|
|
|
=
1, 6625077511 0981371435 9869856452 5407368890 1393900844 … |
|
|
|
||
|
Voir Fractions
continues |
|
|
|
Réduites de racine de 5 Anglais: convergents Voir Réduites |
|
|
|
|
=
0, 5877852522 9247312916 8705954639
0727685976 5243764314 … |
|
|
|
0,
8090169943 7494742410 2293417182
8190588601 5458990288 … |
|
|
Angles en Pi/5, Pi/10 et Pi/20 |
||
|
Nombre d'or Voir Nombre
d'or Convention pour PHI
majuscule et PHI minuscule, parfois inversée |
|
|
|
|
Nombre d'or en puissance. |
|
||
|
Fibonacci et Lucas Réduites: Lucas
au numérateur et Fibonacci au dénominateur. |
|
||
|
Pentagone |
Angle Pi/5
= 72° C'est un des angles
du pentagone |
|
|
Triangle |
|
|
|
Supposons que |
|
||
|
Égalité portée
au carré de chaque côté. |
|
||
|
Le nombre 5,
nombre premier, divise le carré de l'entier p²; il divise aussi le nombre
lui-même*. Le nombre 5 est
un facteur de p. |
|
||
|
En remplaçant: |
|
||
|
Le nombre 5
divise q. Donc, 5 est un facteur de q |
|
||
|
Bilan: les nombres
p et q sont divisibles par 5 et ne seraient donc pas premiers entre eux. |
Contradiction ! Racine de 5 est irrationnelle. |
||
|
Notez ce théorème: |
La racine de tout nombre, non-carré
parfait, est irrationnelle. |
||
Voir Démonstrations
pour racine de 2
* Divisibilité d'un carré
|
Exemple: n² = 3² x 5² = 225 est divisible par 3, 5, 9,
15, 25, 45 ou 75 Alors que n n'est divisible que par les nombres premiers 3 et 5 et par
15, leur produit. Un produit de ses facteurs comportant une puissance ne
divise pas n. On retient à minima: si un nombre
premier divise le carré d'un nombre, il divise ce nombre. Démonstration de si P|Q², avec P premier, alors
P|Q Théorème
fondamental de l'arithmétique: Q est de produit de nombres premiers
distincts:
Q et Q² sont le produit de premiers distincts appartenant à l'ensemble
{P1, P2, …, Pk}. Si P est l'un de ces premiers, il divise à la fois Q et Q². |
La barre verticale signifie divise
|
Racine de 5, irrationnelle – Autre démo |
||
|
Supposons que |
|
|
|
Égalité portée
au carré de chaque côté. |
|
|
|
La quantité de
facteurs d'un nombre au carré est toujours paire. |
p² a une quantité paire de facteurs. q² a une quantité paire de facteurs. |
|
|
Compte tenu de
l'égalité: |
5q² et p² ont les mêmes facteurs, |
|
|
Or, 5, nombre
premier compte pour un facteur. |
5q² a une quantité impaire de facteurs. |
|
|
Bilan: d'un côté
un nombre impair de facteurs et de l'autre un nombre pair: |
Contradiction ! Racine de 5 est irrationnelle. |
|
Merci à Jean-Marc Deshayes
|
Tout d'abord,
c'est évident, mais notez bien que: |
1, 414… + 1, 732… = 3,146… |
|
|
Supposons que ce
nombre soit rationnel. |
|
|
|
Au carré et
calculs |
|
|
|
Au numérateur un
nombre car les produits et différences d'entiers sont des entiers. Au dénominateur
un nombre non nul. |
|
|
|
Or, nous avons démontré
que toute racine est irrationnelle. |
Irrationnel = Rationnel |
|
|
Notre hypothèse
est fausse: |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |