|
|||||||||||||||||||||||||||||||||||
![]()
|
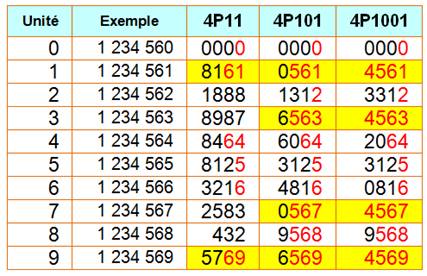
Propriétés des nombres 11, 101 et 1001 Les
nombres en 111 … 1113k sont divisible par 3 >>> Les nombres
101, 1010101 … avec une quantité paire de 1 sont divisibles par 101. Les
nombres 10101, 101010101… avec une quantité impaire de 1 sont divisibles par
un nombre de la forme 111… x 9090…91. Sous
certaines conditions, les nombres élevés à ces puissances conservent leurs
derniers chiffres. |
|
Trouvez
les valeurs de a, b et c telles que: abcabc
/ ababab = 88 / 87 |
|
|
|
|
Les nombres avec unités 1,
3, 7 ou 9 à la puissance 101 conservent leurs trois derniers chiffres
et, à la puissance 1001, ils conservent les quatre derniers. Note: Quel que
soit le chiffre des unités, à la puissance 101 et 1001, ils conservent ce
chiffre des unités.
Cette propriété est utilisée pour le calcul mental de
la racine
treizième. En effet: 1001 = 13 x 77 et les calculateurs prodiges estiment
qu'il est plus facile de calculer la puissance 77ème que la racine
13ème. Ils profitent de
l'équivalence:
|
|
|
|
|
|
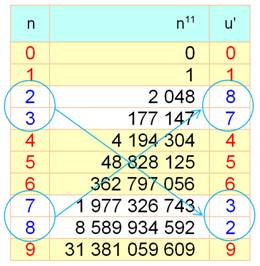
Tableau
des valeurs de u' en fonction de u
Ce
qui confirme notre premier tableau, colonne puissance 11.
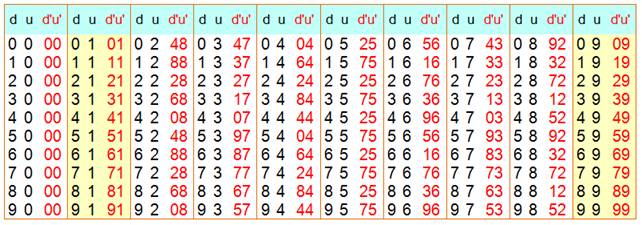
Tableau
des valeurs de d'u' en fonction de du
Ce
qui confirme notre premier tableau, colonne puissance 11.
Un
calcul plus avancé donne:
Confirmant
le chiffre des unités qui se termine comme u11. Mais le
chiffre des dizaines est encore
difficile à estimer à partir de cette expression. Avec
u = 1:
les deux derniers chiffres sont conservés. Avec
u = 9 = 10 – 1 :
les deux derniers chiffres sont conservés. Note:
le développement de (10 – u)10 se termine par 100u9 +u10 |
|
|
Question Trouvez
les valeurs de a, b et c telles que: abcabc
/ ababab = 88 / 87 Solution Vous
avez reconnu les répétions telles que:
La
fraction des deux nombres devient:
Soit
les valeurs: a = 2, b =
9 et c = 6. Commentaires Seules
quatre fractions jusqu'à 100 sont compatibles de cette énigme: 55/54, 75/74,
77/75 et 88/87. Par contre, il existe de nombreuses possibilités au-delà. Un
exemple: 143/144 qui donne 481/48. |
![]()
![]()