|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Humour
Voir Pensées & humour |
Sciences En
2019, les chercheurs du MIT ont Pour
cela, ils ont construit une réplique des nœuds à base de fibres optiques qui
changent de couleur selon les contraintes exercées. Ce
modèle permet de prévoir la tenue et la stabilité des nœuds. |
|
Nœuds en mathématiques Entrelacs – Tresses (nattes)
La
théorie des nœuds, branche de la topologie,
s'intéresse à la forme des nœuds et non à leur longueur, y compris par
déformation sans déchirure ni cassure. Cette
théorie est née au XIXe siècle avec Gauss. Henri Poincaré
développe la topologie algébrique incluant la notion de nœud. Ses
applications nouvelles en biologie comme en cosmologie ont accéléré son
développement ces trente dernières années. Ces animaux, sont-ils laineux (les nœuds) ? |
|
Nœud: en mathématiques, un nœud
est similaire à un simple nœud physique, à la différence notable que ses deux
extrémités sont reliées l'une à l'autre. Ces nœuds ressemblent donc à des
boucles enchevêtrées, puisqu'ils ne possèdent pas de bouts. Cordage: terme générique. Bout: une corde. Amarre: cordage servant à
tenir le bateau le long du quai. Courant: partie du cordage
avec laquelle on forme un nœud: brin de travail. Dormant: l'autre partie du
cordage: brin mort. Frapper une amarre:
immobilisation de l'amarre avec un nœud, sur un taquet par exemple. Lover un cordage:
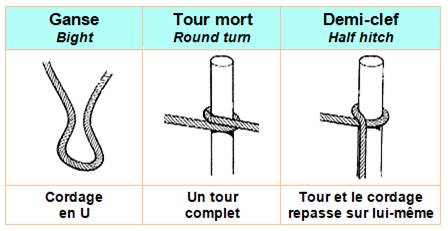
l'enrouler pour le ranger. Ganse: un demi-tour fait
sur le cordage. Lui donner une forme en U. Tour mort: tour de cordage
autour d'un point fixe. Simple tour effectué par un cordage autour d'un objet
et ayant un effet de frein. Demi-clef: tour mort avec
cordage repassant sur lui-même. Voir
Demi / Demi en
mots
|
|
|
||||
|
3 800:
quantité
de nœuds recensés: nœud chaise, cabestan, d'arrêt, Zeppelin, demi-clef,
d'évadé … Exemple
de nœud en huit
Voir
Nombre
8 et culture |
Voir
Explications sur le site de
Laurent Rosenfeld |
|||
|
Six
grandes catégories de nœuds |
||||
|
Catégorie |
Type |
Exemples |
||
|
Nœuds d'arrêt |
Demi-Nœud |
|
||
|
Nœuds de liure |
Nœud
plat |
|
||
|
Nœuds coulants |
Nœud
du pendu |
|
||
|
Nœuds à boucle |
Nœud
de chaise |
|
||
|
Nœuds à raccourcir |
Nœud
de plein poing |
|
||
|
Nœuds d'amarrage |
Nœud
de cabestan |
|
||
![]()
Les problèmes de la théorie des nœuds
|
1.
Trouver une méthode pour décider si deux
nœuds sont équivalents; 2.
Trouver un algorithme pour décider si un
nœud est noué; et 3.
classifier les nœuds non équivalents. |
|
Mark
Lakcenby (Université d'Oxford) Vient de trouver un algorithme quasi-polynomial
pour déterminer si deux nœuds
sont équivalents, résolvant une question centenaire. On cherche à dénouer une courbe définie dans l’espace
tridimensionnel (une ficelle emmêlée et nouée aux deux bouts, par exemple,
soit: une courbe fermée en trois dimensions). Depuis 1961, il a été démontré (Wolfgang Haken) qu'il
existe toujours un tel algorithme. Tous les algorithmes développés depuis
lors opéraient en temps exponentiel. On a prouvé que problème du voyageur de
commerce est NP-difficile
(pas d'algorithme polynomial). On ne savait pas décider du statut du problème
du dénouage de nœuds : exponentiel ou polynomial. Désormais, il existe une
solution quasi-polynomiale. Voir
son exposé: Unknot
recognition in quasi-polynomial time Voir
Première
preuve d'un algorithme de dénouage rapide – Philippe Pajot – La Recherche |
|
Anglais In a remarkable Gordian tour-de-force,
Oxford Mathematician Marc Lackenby has created an algorithm that determines
whether a knot is the unknot in n^{c log(n)} steps, for some constant c,
which is known as quasi-polynomial time. This is only slightly slower than
polynomial time, and represents a significant advance over what previously
was known. Marc Lackenby announces a new
unknot recognition algorithm – Oxford Mathematical Institute |
Voir Actualités mathématiques / Anglais pour le bac et pour les affaires
Quelques nœuds typiques
|
|
|||
|
Le plus
vieux nœud |
Retrouvé sur des filets de
pêche vers 8000 av. J.-C. |
||
|
Vandermonde (1735-1796) |
Aborde les nœuds dans son
livre: Remarques sur les problèmes de situation. Un début en ce qui deviendra
la topologie. |
||
|
Carl
Friedrich Gauss (1777-1855)
|
Le premier à véritablement
étudier les nœuds. Il s'intéresse au nombre
d'entrelacs pour une paire de nœuds.
En 1833, il montre que le nombre d'entrelacs pouvant être formés à
partir de deux nœuds se calcule au moyen d'une intégrale. |
||
|
Johann
Benedict Listing |
Étudiant de Gauss qui va
créer le mot topologie (de topos, lieu et logos, étude ou doctrine, lequel
vient de legein, parler). |
||
|
Lord
Kelvin (1824-1907) |
Modèle de la matière: les
atomes sont représentés par des tourbillons en forme de nœuds dont la nature détermine
les propriétés de l'élément chimique, notamment l'absorption ou l'émission de
lumière. Théorie abandonnée avec la connaissance de la classification
de Mendeleïev (1869). |
||
|
Peter
Guthrie Tait (1831-1901) |
Collaborateur de Kelvin, et
reprenant une idée du révérend Thomas Kirkman, il propose la première
classification des nœuds jusqu'à dix croisements en y passant vingt ans de sa
vie. |
||
|
C.N.
Little |
En 1889, après six ans de
travail, il publie une liste de 43 nœuds non-alternés de 10 croisements. En
1974, la liste est validée à deux nœuds près qui s'avérèrent identiques. Il a aussi travaillé sur les
nœuds à onze croisements. |
||
|
Perko |
Il a travaillé sur la
duplication et a laissé son nom aux paires de Perko. |
|
|
|
Henri
Poincaré (18(4-1912) |
Fondateur de la topologie
algébrique avec son ouvrage: Analysis Situ. Recherche d'invariants dans les
transformations. |
||
|
Alexander
et Briggs |
En 1927: preuve que tous les
nœuds jusqu'à neuf croisements sont bien distincts. Seuls quelques uns
impossibles à discriminer. Ce sont les premiers à
appliquer des invariants polynomiaux. |
||
|
Kurt
Reidemeister |
En 1932: classification
rigoureuse des nœuds jusqu'à neuf croisements. |
||
|
(1898-1962) |
Le père de la théorie des tresses. |
||
|
John
Conway |
En 1969, il invente une
nouvelle notation des nœuds et détermine tous les nœuds jusqu'à onze
croisements. |
||
|
Ordre 16 |
En 1978, Alain Caudron
(France) corrige quelques erreurs de la table de Conway Hugh Dowker invente une
nouvelle notation. Son application aa été programmée par Morwen Thistlethwaite qui aboutira
à tous les nœuds jusqu'à l'ordre 12 en 1981 et 13 en 1982 puis plus tard,
avec des ordinateurs plus puissants, jusqu'à 16. Jim Hotste et Jeff Weeks, avec une méthode différente,
arrivèrent aussi à l'ordre 16. |
||
|
Vaughan
Jones |
Médaille Fields en 1984 pour
son invention d'un nouvel invariant. Kauffman a démontré l'invariance du
polynôme de Jones. D'autres polynômes plus
puissants ont été crées depuis comme celui de Homfly. |
||
|
|
|||
|
Équivalence |
Deux nœuds sont équivalents
si on peut amener l'un sur l'autre par déformation sans rompre la courbe. |
||
|
Invariant |
Quantité (ou même polynôme), qui associé à d'autres,
permet de caractériser deux nœuds équivalents. Aucun des invariants définis
actuellement ne permet de décider si deux nœuds sont équivalents. Cependant deux nœuds sont
surement différent si leurs invariants sont différents. |
||
|
Invariant avec les croisements |
Invariant le plus classique.
On recherche le nombre minimal de croisements. Ce qu'a fait Peter Tait. |
||
|
Invariant avec polynôme |
Les invariants polynômes caractérisent
la suite des déformations d'un nœud (destructions de croissements, torsion
vers la droite …) |
||
|
Entrelacs |
Enchevêtrement de nœuds. Un
entrelacs à deux composantes est formé de deux cordes fermées. |
|
|
|
Tresse (ou natte) Théorie des tresses |
Une tresse
est formée de k brins qui réunissent 2k extrémités. Les brins peuvent passer
les uns sur les autres, mais ne jamais revenir en arrière. |
|
|
|
Somme de deux nœuds orientés |
On coupe chacun et on recolle
en respectant l'orientation.
|
||
|
Nœud premier |
S'il est non trivial et si on
ne peut pas le décrire comme somme de deux nœuds non triviaux. |
||
|
Nœud gansé |
Nœud qui se défait en tirant
sur l'extrémité gansée (nœuds coulant). |
||
|
Image miroir |
Image obtenue en inversant
tous les croisements.
|
||
|
Nombre gordien |
Invariant
obtenu en coupant la courbe autant de fois que nécessaire, mais un minimum de
fois, pour aboutir à une boucle. En théorie des nœuds, nombre qui permet de
rendre compte de la complexité d'un nœud. "Il permet par exemple de
contrôler un nombre qu'on appelle le nombre gordien et qui a un sens évident.
On essaie de faire traverser un brin à travers un autre jusqu'à ce que le
nœud soit dénoué, et on compte le nombre de brins qu'il faut faire traverser
pour arriver à dénouer le nœud." — Jean-Pierre Changeux & Alain Connes,
Matière à pensée, Odile Jacob, 1989. Source Wiktionnaire |
||
|
Nœud trivial ou |
La circonférence d'un cercle
ou toute autre déformation de celle- ci. Soit, une ficelle réunie aux
extrémités, sans nœud. Anglais:
unknot |
|
|
|
Nœud le plus classique |
Le trèfle: nœud a trois
croisements. Anglais:
Trefoil knot |
|
|
|
Nœud de huit |
Le nœud de huit est
caractérisé par quatre croisements |
|
|
|
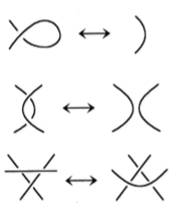
Mouvements de Reidemeister |
Trois mouvements qui
préservent l'équivalence des nœuds. |
|
|
|
Théorème fondamental de la théorie
des nœuds |
Deux nœuds sont équivalents
si et seulement si on peut les transformer l'un dans l'autre par un nombre
fini de mouvements de Reidemeister. |
||
|
|
||
|
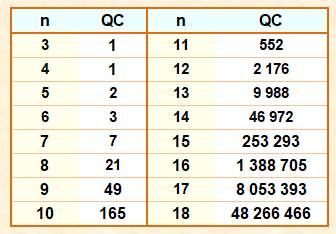
Tous les
nœuds connus jusqu'à l'ordre 16 => Ne sont
pas comptés les nœuds obtenus pas effet miroir s'ils sont équivalents. On ne
connait pas la quantité pour l'ordre 17. On ne
connait pas de formule prédisant la quantité de nœuds en fonction de l'ordre. Curieusement,
on ne sait pas démontrer qu'il y plus de nœuds à l'ordre suivant. Il y a 247
jusqu'à 10 croisements et 1 701 935
jusqu'à 16. |
Quantité
de nœuds premiers selon n croisements
Voir OEIS A002863 |
|
Le
premier numéro donne la quantité de croisements (l'ordre).
L'indice
est une simple indication pour distinguer les nœuds de même ordre.

|
En
1999, Yong Mao et Thomas Fink (Université de Cambridge) comptaient 85 nœuds de
cravate. En
2014, une équipe de mathématicien, conduite par Mikael Vejdemo-Johansson de
l'Institut Royal de Technologie de Stockholm, a calculé qu'il existe, en fait,
177 147 façon de nouer une cravate. |
Nœud de Conway – 11 croisements
|
Idée sur le sujet: La question était
de savoir s’il s’agissait d’une tranche (slice). C’est-à-dire, si ce nœud
pouvait être obtenu en Lisa Picirillo a comparé ce nœud à
un nœud semblable de son cru, plus tarabiscoté, mais plus facile à
appréhender. Or, celui-ci n'est pas tranche, le nœud de Conway ne l'est pas non plus. Ceci complète la classification de
tous les nœuds de ce type jusqu'à douze croisements.
|
Voir Nombre 11
Source Graduate Student Solves Decades-Old
Conway Knot Problem – Quanta magazine
et autres journaux de juin 2020
|
Demande
en mariage façon américaine: "je ne peux pas me marier sans toi à mes
côtés. Veux-tu être ma femme?" To
tie the knot: lier le nœud, et au figuré, passer la corde au cou, se marier. Snarl:
nœud |
|
Voir Pensées
& humour / Anglais –
Bagage minimum
Nœud de Escher

Voir Escher
|
La
théorie des nœuds est un domaine très vaste et pointu de la topologie. Voyez
la définition mathématique du nœud: Tout
nœud est la frontière d'une surface orientée dans R3. Domaine
qui demeure à la pointe de la recherche tant les applications sont
nombreuses.
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Sites anglais |
|
|
Cette page |
![]()