Signature première des nommbres

Édition du: 21/03/2021

M'écrire

Brèves de Maths

INDEX

Factorisation

Facteurs et diviseurs

Nombres et leurs facteurs

Facteurs

Nombres riches

Conjecture

Commentaires

Signature

SIGNATURE PREMIÈRE des nombres

Prime signature

Tout nombre peut être mis sous la forme d'un produit de facteurs premiers, chacun porté à une puissance. Le produit des facteurs "nus" est le radical du nombre; la liste ordonnée des puissances est sa signature première.

Terminale et plus

Sommaire de cette page

>>> Approche

>>> Radical et signature des nombres de 1 à 100

>>> Types de nombres selon leur signature

>>> Propriétés

Débutants

Multiplication

Glossaire

Facteurs et diviseurs

APPROCHE

haut

Pour les nombres de 100 à 105, on donne la décomposition en facteurs et la liste des exposants des facteurs.

Cette liste est la signature du nombre.
Exemple: signature(100) = [2, 2]

Les nombres 101 et 103 sont premiers. leur signature est [1].

Attention: la liste est triée par ordre croissant
12 = 2². 3 et sa signature est [1, 2] et non [2, 1].

Nombre, factorisation, [signature]

Radical et signature des nombres de 1 à 100

En ocre les nombres premiers et en jaune les puissances pures

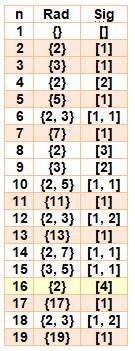
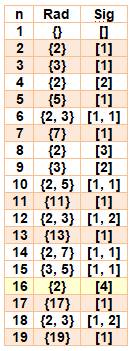
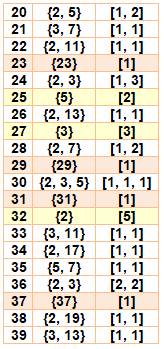
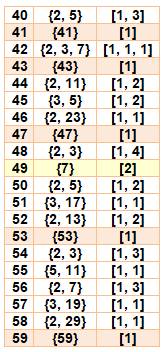
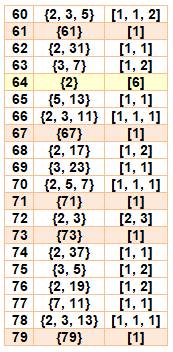
Types de nombres selon leur signature				haut
Signature	Exemple	Début de liste	Nom et lien
[1]	13 = 1 x 13	2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …	Nombres premiers >>>
[1, 1]	10 = 2 x 5	6, 10, 14, 15, 21, 22, 26, 33, 34, 35, …	Nombres à deux facteurs distincts: nombres semi-premiers sans carré >>>
[1, 1, 1]	30 = 2 x 3 x 5	30, 42, 66, 70, 78, 102, 105, 110, 114, 130, …	Nombres à trois facteurs distincts: nombres sphéniques >>>
[1, 1, 1, 1]	210 = 2 x 3 x 5 x 7	210, 330, 390, 462, 510, 546, 570, 690, 714, 770, …	Nombres à quatre facteurs distincts.
[2]	25 = 5²	4, 9, 25, 49, 121, 169, 289, 361, 529, 841, 961, …	Nombres carrés >>>
[1, 2]	50 = 2 x 5²	12, 18, 20, 28, 44, 45, 50, 52, 63, 68, …	Carré d'un nombre premier par un facteur premier.
[2, 2]	100 = 2² x 5²	36, 100, 196, 225, 441, 484, 676, 1089, 1156, …	Produit de deux carrés de nombres premiers.
[2, 2, 2]	900 = 2² x 3² x 5²	900, 1764, 4356, 4900, 6084, 10404, …	Produit de trois carrés de nombres premiers.
[3]	125 = 5³	8, 27, 125, 343, 1331, 2197, 4913, 6859, …	Nombres cubes >>>
[1, 3]	88 = 2³ x 11	24, 40, 54, 56, 88, 104, 135, 136, 152, 184, …	Cube d'un nombre premier par un facteur premier.
[2, 3]	200 = 2³ x 5²	72, 108, 200, 392, 500, 675, 968, 1125, …	Carré par cube de nombres premiers. Nombres d'Achille.
[3, 3]	1000 = 2³ x 5³	216, 1000, 2744, 3375, 9261, 10648, 17576, 35937, …	Cube par cube de nombres premiers.
[4]	625 = 5⁴	16, 81, 625, 2401, 14641, 28561, 83521, …	Nombres bicarrés >>>

Suite et liste plus complète en: Table des nombres 1 à 1000 classés par type de signature

Propriétés

haut

Nombre 1

Par définition sa signature est [1].

Fonctions arithmétiques

De nombreuses fonctions arithmétiques se déduisent (sont fonction) de la signature du nombre.

Par exemple: la quantité de diviseurs est égale u produit des nombres de la signature incrémentés de 1.
Exemple avec le nombre 60

*Facteurs*	2² x 3 x 5
*Signature*	[2, 1, 1]
*Tau*	3 x 2 x 2 = 12
*Diviseurs*	{1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}

Tête de liste

Le premier nombre de chaque type de signature est un produit de primorielles. A025487

Haut de page

Retour	Facteurs et diviseurs Fonctions arithmétique
Suite	Table des nombres 1 à 1000 classé par type de signature Nombres d'Achille Nombres puissants
Voir	Conjecture ABC Nom des nombres Nombres et leur quantité de facteurs (uniques et répétés) Nombres selon leur nom Table des facteurs et diviseurs des nombres (1 à 1000) Types de nombres premiers et cousins Types de nombres selon diviseurs Types de nombres selon leur factorisation – Index
Sites	Prime signature – Wikipedia Prime signature – Wolfram MathWorld
OEIS	A000040 Prime numbers A001248 Squares of prime numbers A006881 Two distinct prime divisors (square-free semiprimes) A007304 Three distinct prime divisors (sphenic numbers) A030078 Cubes of prime numbers A030514 Fourth powers of prime numbers A050997 Fifth powers of primes A054753 Squares of primes times another prime A065036 Cubes of primes times another prime A085986 Squares of square-free semiprimes
Cette page	http://villemin.gerard.free.fr/aMaths/Factorisation/Signatur.htm

Haut de page