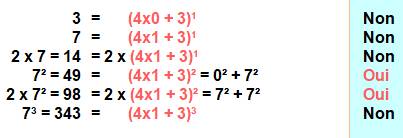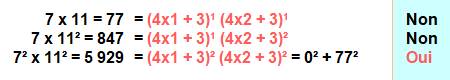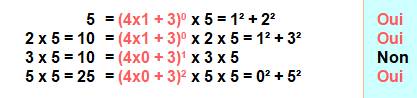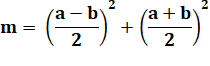somme de carrés - théorème de caractérisation

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/03/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Carrés	SOMME de CARRÉS			Glossaire Carrés
INDEX Accueil Sommaire Carrés	1 et 2 carrés	Introduction	Premières idées	Table 1 à 100
	1 et 2 carrés	Théorème	Quantité
	3 et 4 carrés	Somme 3 carrés	Somme 4 carrés
		Sommaire de cette page >>> Approche >>> Nombres somme de 2 carrés >>> Trouver la somme >>> Nombre double: 2m = a² + b² >>> Nombre m = a² + b² + 1²

SOMME de deux CARRÉS

Théorème

Tout nombre premier de la forme 4n + 1 est la somme de deux carrés.

Anglais: sum of two square problem or Girand's problem (1627)

En bref

Théorème des deux carrés de Fermat – Nombres premiers

Tout nombre PREMIER est la somme de deux carrés de façon unique si et seulement si il est de la forme 4n + 1.

Fermat, démontré par Euler

Théorème des deux carrés – Nombres quelconques

Un entier est somme de deux carrés si et seulement si chacun de ses facteurs premiers de la forme 4k + 3 est à une puissance paire.

De plus, la décomposition est unique si aucun facteur n'est en 4k + 1, ou alors un seul à la puissance unité.

Théorème des deux carrés de Jacobi

Un nombre entier avec K diviseurs en k + 1 et K' en 4k + 3 (diviseurs non nécessairement premiers). Alors, la quantité Q de toutes les représentations en somme de deux carré est égale à: Q = 4 (K + K').

Voir Structure des nombres premiers

Approche
Observation Nous avons observé que les nombre en 4k + 3 ne sont jamais somme de 2 carrés. Y a-t-il anguille sous roche? Voyons quelques nombres sous cet angle. Se référer à la table pour connaître la décomposition d'un nombre en somme de 2 carrés.
Avec un terme en 4k + 3 Jamais somme de deux carrés avec un terme simple 4k + 3 Par contre en élevant ce terme au carré, cela devient possible. Voyons, à la puissance 3: raté!
Avec deux termes en 4k + 3 Ils ont beau être deux de cette forme, ça ne marche pas. Un seul au carré, non plus. Il faut les deux au carré pour obtenir une somme de 2 carrés.
Une question de puissance? C'est bien vu: il faut que le terme en 4k + 3 soit à une puissance paire pour obtenir une décomposition. Et, cela est vrai de tous les facteurs en 4k + 3: tous doivent être à une puissance paire.

Bilan

Un seul facteur en 4k + 3 ou en 4k + 3 à une puissance impaire

suffit pour annuler toute possibilité d'être un nombre somme de deux carrés.

Théorème de la somme de deux carrés
Soit la décomposition canonique d'un nombre en facteurs premiers Un nombre est somme de deux carrés si et seulement si chacun de ses facteurs premiers de la forme 4k + 3 a un exposant pair.	Si, lorsque p_i = 4k + 3, ₁ est pair; Alors n est somme de 2 carrés. Autrement dit: h(n) = 1.
La démonstration fait appel à la théorie des résidus quadratiques. Cette théorie n'est pas encore développée sur ce site et sans les bases de cette théorie, la démonstration serait trop complexe à expliquer (même avec, d'ailleurs!).

Voir Autre formulation de ce théorème

Théorèmes des deux carrés de Fermat

Tout nombre premier impair est la somme de deux carrés si et seulement s'il est de la forme 4n + 1.

La somme des carrés est alors unique.

Une condition nécessaire pour qu'un nombre entier soit la somme de deux carrés est que tous ses facteurs premiers soient de la forme 4n + 1.

Trouver la somme
Astuce Une astuce consiste à utiliser l'identité de Fibonacci - Lagrange (a² + b²) (c² + d²) = (ad + bc)² + (ac - bd)² Exemple
Pour l'exemple, prenons un nombre ayant des facteurs en 4k + 3 à une puissance paire. Regroupons les termes de manière à minimiser la valeur du produit, tout en conservant un terme en 4k + 3 à une puissance paire dans chaque parenthèse. Décomposez chaque terme en somme de 2 carrés. Appliquez l'identité.	2 x 3² x 5 x 7² = 4 410	= (2 x 7²) (3² x 5) = 98 x 45 = (7² + 7²) (3² + 6²) = (42 + 21)² + (21 – 42)² = 63² + 21²

Nombre double: m = a² + b²

Si 2m est la somme de deux carrés,

alors m l'est aussi.

La preuve découle du fait que x et y sont forcément de même parité. Leur somme et leur différence sont divisibles par 2.

Exemple

2m = 2² + 4² = 20

m = 1² + 3² = 10

Nombre m = a² + b² + 1²
Si p est premier (sauf 2), il existe k < p tel que: a² + b² + 1² = k.p Vrai également si p est un nombre impair. Ce qui veut dire que pour tout nombre premier, un de ses multiples est somme de trois carrés, et a fortiori de quatre carrés. Ce qui constitue un élément de preuve de la somme de quatre carrés.		Exemple pour 7 2 x 7 = 14 = 2² + 3² + 1 3 x 7 = 21 = 2² + 4² + 1 5 x 7 = 35 = 3² + 5² + 1 6 x 7 = 42 = 4² + 5² + 1 Exemple pour 11 1 x 11 = 11 = 1² + 3² + 1 3 x 11 = 33 = 4² + 4² + 1 6 x 11 = 66 = 1² + 8² + 1 = 4² + 8² + 1 9 x 11 = 99 = 7² + 7² + 1 10 x 111 = 110 = 3² + 10² + 1
Démonstration de la propriété 1 Avec p = 2n + 1, formons les deux ensembles		A { a² avec a de 0 à n} B {–b² – 1 avec b de 0 à n}
Dans A, il n'y a pas de couples congruent mod p
Si c'était le cas, on aurait les divisibilités suivantes:
Or a – c comme a + c sont inférieurs ou égaux à 2n et donc à p.
Démonstration de la propriété 2
Avec le même procédé on démontre que: Dans B, il n'y a pas de couples congruent mod p.
Démonstration de la propriété 3 Aucun élément commun entre A et B		Les éléments de A sont positifs alors que ceux de B sont négatifs.
La réunion des deux ensembles compte 2n + 2 = p + 1 éléments.		Il y a n + 1 éléments dans A, et n + 1 autres éléments dans B
Chacun de ces éléments, divisé pas p, donne au maximum p restes, or il y p + 1 valeurs		Il y a forcément deux restes identiques (principe des tiroirs) On dit: il existe deux éléments, un de A et un de b qui sont congruents modulo p.
Résultat mis en forme: a² + b² + 1 divisible par p; autrement-dit, ce nombre est multiple de p.
La valeur de k est inférieure à p.	Sachant que a et b varient de 0 à n: