type de nombres: nombres premiers

INDEX Types de premiers Premiers Nombres Types de nombres	Nombres premiers
	Premiers	Presque Premiers	Probablement P.
	Premiers équilibrés	Premiers forts	Cube (cuban)
	Premiers bons	Premiers inévitables	Multi premier
	Emirp et circulaires	Résistants	Combinaisons

NOMBRES PREMIERS

Sommaire de cette page

>>> Nombres premiers

>>> Liste de 0 à 1100

>>> Jumeaux et quadruplets

>>> Nombres premiers selon leur unité

>>> Liste des premiers en 7

>>> Nombres premiers ondulants à deux chiffres

>>> Sommes et produits des nombres premiers

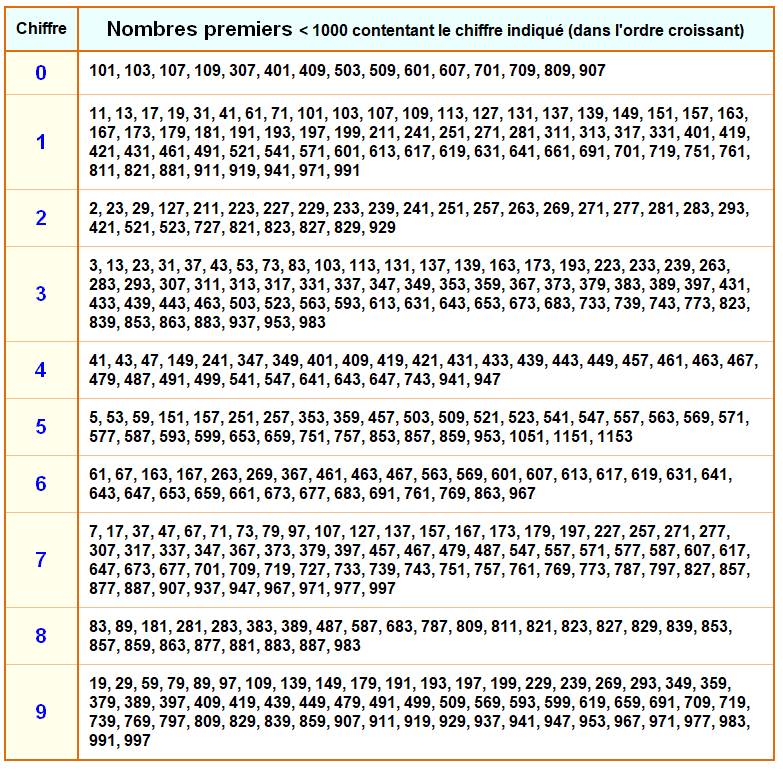
>>> Nombres premiers contentant un chiffre donné

Débutants

Premiers

Glossaire

Premiers

Famille

Nombre / Diviseurs / Multiplicatif / …

… / Types de nombres premiers et cousins

Jumeaux / Quadruplets

Approche

Si avec n petits carrés, il n'est possible de créer qu'une rangée de carrés et non un rectangle, alors le nombre n est un nombre premier.

Si avec n petits cubes de 1 cm de côté, je ne peux construire qu'une pile et non pas un rectangle ou un parallélépipède, alors n est un nombre premier.

Une rangée (une ligne)

Pas de rectangle

Exemples

5 = 1 x 5 = 5 x 1 Uniques possibilités de former le nombre entier 5 avec un produit.

11 = 1 x 11 = 11 x 1 Uniques possibilités de former le nombre entier 11 avec un produit.

Définitions

NOMBRES PREMIERS

Entiers naturels divisibles par 1 ou par lui-même exclusivement.

Diviseurs de n premier

1 et n

Facteurs de n premier

1 et n

Factorisation de n premier

n = 1 x n

Particularité

0 et 1 sont des nombres un peu à part: ni premiers, ni composés.

Propriétés

Un nombre premier ne comporte que deux diviseurs: 1 et n.

La somme des diviseurs est toujours: n + 1.

Il existe une infinité de nombres premiers.

Quelques propriétés:

Entre n et 2n,

il y a toujours

un nombre premier

Un nombre pair (>2)

est toujours la somme

de 2 premiers

Un nombre impair (>5)

est la somme de

3 premiers

Entre 222 et 444,

307 est premier

48 = 31 + 17

34 = 29 + 5

55 = 5 + 19 + 31

Voir Conjecture de Goldbach

Fondamental

Les nombres premiers sont les briques de construction de tous les nombres.

Ce sont des briques toutes différentes et peu prévisibles en taille!

Mais, la beauté est que:
tout nombre est le produit UNIQUE de nombres premiers
(outre l'ordre dans lequel on place les facteurs).

C'est le théorème fondamental de l'arithmétique.

Anglais

Prime numbers

An integer greater than one is called a prime number if its only positive divisors (factors) are one and itself

For example, the prime divisors of 10 are 2 and 5

The first six primes are 2, 3, 5, 7, 11 and 13

The Fundamental Theorem of Arithmetic shows that the primes are the building blocks of the positive integers: every positive integer is a product of prime numbers in one and only one way, except for the order of the factors

This is the key to their importance: the prime factors of an integer determine its properties

(Extract from Chris K. Caldwell pages, the worldwide expert in prime numbers)

Voir

Premiers – Débutants

Premiers – Glossaire

Premiers – Introduction et développements

Premiers – Théorèmes

Barre magique des nombres premiers

Aiguillage vers tous les sujets concernant les nombres premiers.

Tous les types de nombres premiers.

Aussi

Théorème fondamental / Démonstration

Représentation des nombres

Types de nombres premiers

JUMEAUX

QUADRUPLETS

UNIQUES

Tous les autres: Types de nombres premiers et cousins

Nombres premiers de 0 à 1100
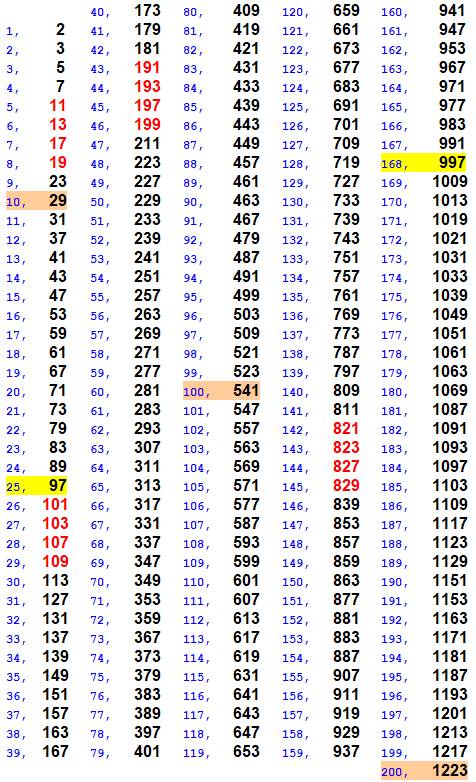
Liste des nombres premiers de 0 à 1100 avec leur rang en bleu Il y a 25 nombres premiers < 100 168 < 1000 Notez que 2 est le seul nombre premier pair et que 5 est le seul à être terminé par 5. À partir de 7 tous les nombres premiers sont terminés par 1, 3, 7 et 9. Les dizaines sont un témoin de ces finales: 11, 13, 17, 19 sont premiers Même chose pour 101, 103, 107, 109 Notez également les nombres premiers séparés de 2 seulement Ce sont les premiers jumeaux comme 29 et 31, 41 et 43, etc.
Premiers de Honaker Tels que la somme de ses chiffres et celle de son indice sont égales. Ex: 263 = P₅₆ et 2+6+3 = 5+6 = 11	[131, 32], [263, 56], [457, 88], [1039, 175], [1049, 176], [1091, 182], [1301, 212], [1361, 218], [1433, 227], [1571, 248], [1913, 293], [1933, 295], [2141, 323], [2221, 331], [2273, 338], [2441, 362], [2591, 377], [2663, 386], [2707, 394], [2719, 397], [2729, 398], [2803, 409], [3067, 439], [3137, 446], [3229, 457], [3433, 481], [3559, 499], [3631, 508], [4091, 563], [4153, 571], [4357, 595], [4397, 599], [4703, 635], [4723, 637], [4903, 655], [5009, 671], [5507, 728], [5701, 751], [5711, 752], [5741, 755], [5801, 761], [5843, 767], [5927, 779], [6301, 820], [6311, 821], [6343, 826], [6353, 827], [6553, 847], [6563, 848], [6653, 857], [6737, 869], [6827, 878], [6971, 896], [7013, 902], [7213, 922], [7283, 929], [7411, 940], [7481, 947], [7523, 953], [7741, 982]

Voir Jusqu'à 10 000 / Barre magique des premiers

Liste des premiers plus petits et plus grands de k chiffres

En jaune égalité k = r telle que par exemple: 10²³ – 23 est premier

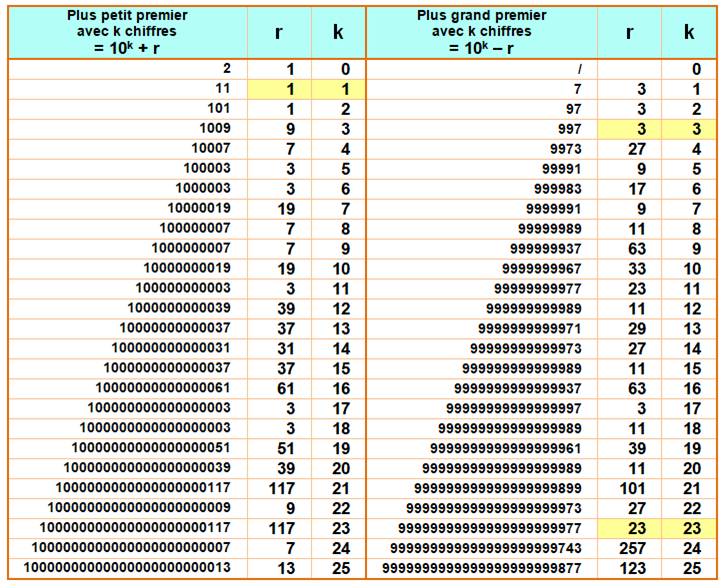
Égalités k = r suivantes pour "plus petit" avec k = 451 et pour "plus grand" pour k = 171

Seules jusqu'à k = 500

Voir Table des nombres premiers du ième rang

Produit et somme des nombres premiers

Exemple: 2×3×5×7 = 210; 2+3+5+7 = 17; 210–17 = 193; 210+17 = 227

Nombres premiers par 2 (jumeaux) et par 4(quadruplets)

Jumeaux

Les 200 en-tête de liste

1, 3 26, 569 51, 1607 76, 2687

2, 5 27, 599 52, 1619 77, 2711

3, 11 28, 617 53, 1667 78, 2729

4, 17 29, 641 54, 1697 79, 2789

5, 29 30, 659 55, 1721 80, 2801

6, 41 31, 809 56, 1787 81, 2969

7, 59 32, 821 57, 1871 82, 2999

8, 71 33, 827 58, 1877 83, 3119

9, 101 34, 857 59, 1931 84, 3167

10, 107 35, 881 60, 1949 85, 3251

11, 137 36, 1019 61, 1997 86, 3257

12, 149 37, 1031 62, 2027 87, 3299

13, 179 38, 1049 63, 2081 88, 3329

14, 191 39, 1061 64, 2087 89, 3359

15, 197 40, 1091 65, 2111 90, 3371

16, 227 41, 1151 66, 2129 91, 3389

17, 239 42, 1229 67, 2141 92, 3461

18, 269 43, 1277 68, 2237 93, 3467

19, 281 44, 1289 69, 2267 94, 3527

20, 311 45, 1301 70, 2309 95, 3539

21, 347 46, 1319 71, 2339 96, 3557

22, 419 47, 1427 72, 2381 97, 3581

23, 431 48, 1451 73, 2549 98, 3671

24, 461 49, 1481 74, 2591 99, 3767

25, 521 50, 1487 75, 2657 100, 3821

Quadruplets

en 1, 3, 7 et 9 de 0 à 50 000

101

191

821

1 481

1 871

2 081

3 251

3 461

5 651

9 431

13 001

15 641

15 731

16 061

18 041

18 911

19 421

21 011

22 271

25 301

31 721

34 841

43 781

Nombres premiers selon leur unité

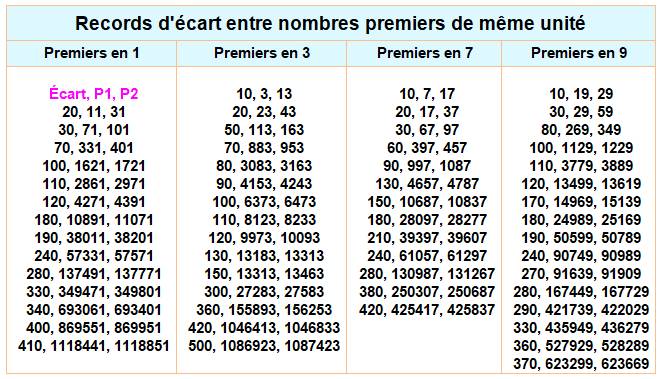
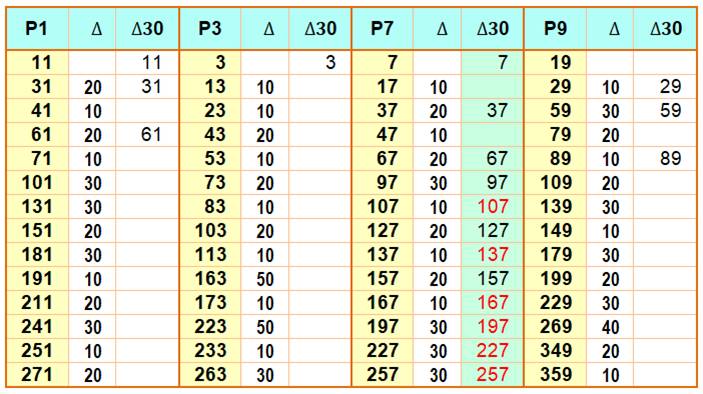
Delta pour écart et Delta 30 pour progression en 30

Notez la double-progression en 30 des premiers en 7:
{7, 37, 67, 97, 127, 157} et {107, 137, 167, 197, 227, 257}

Liste des premiers en 7 et identification de multi-écarts de 30

7, 17, 37, 47, 67, 97, 107, 127, 137, 157, 167, 197, 227, 257, 277, 307, 317, 337, 347, 367, 397, 457, 467, 487, 547, 557, 577, 587, 607, 617, 647, 677, 727, 757, 787, 797, 827, 857, 877, 887, 907, 937, 947, 967, 977, 997, 1087, 1097, 1117, 1187, 1217 ….

Il faut attendre 7 457 à 7 607 pour trouver une nouvelle progression de six premiers de raison 30.

Voir Nombres premiers en progression arithmétique

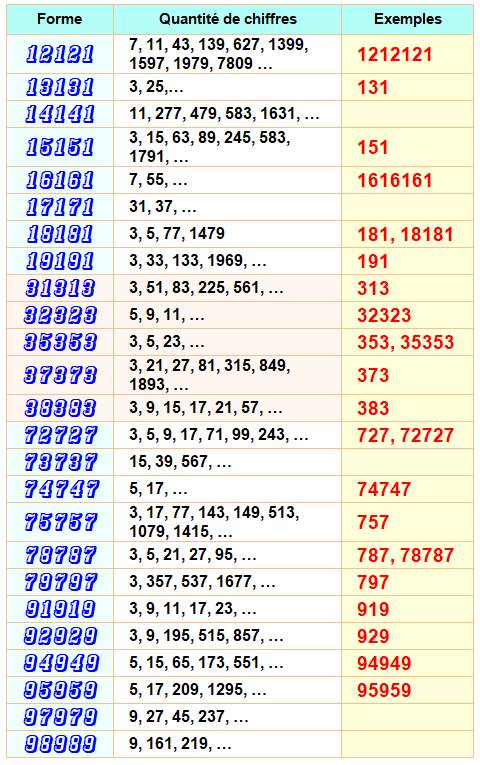
Nombres premiers ondulants à deux chiffres

Nombre premiers ondulants sur deux chiffres:

Forme: indique la répétition des deux chiffres;

Quantité de chiffres formant le nombre premier.
Ex: avec 11 chiffres 12121212121 est un nombre premier; et

Exemples: nombres premiers ondulants jusqu'à 7 chiffres.

La première forme en 12121 a été testée jusqu'à une quantité de 10 000 chiffres, les autres jusqu'à 2 000 chiffres. Le pointillé indique donc que le nombre suivant aura plus de 2 000 chiffres. Si la forme n'est pas présente, c'est qu'il n'y a pas de nombres pemiers de cette forme.

Cas de 101: c'est le seul nombre premier de cette forme: 10101 est divisible par 3

Bilan pour les nombres premiers ondulants à trois et cinq chiffres

101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929.

18181, 32323, 35353, 72727, 74747, 78787, 94949, 95959.

Voir Nombres ondulants

Somme des dix plus petits premiers contenant chacun des chiffres

101 + 11 + 2 + 3 + 41 + 5 + 61 + 7 + 83 + 19 = 333

Voir	Combinaisons entre nombres premiers Somme et produits des nombres premiers successifs Forme avec produit de deux premiers consécutifs Produit de premiers consécutifs + 1 Semi premiers Presque Premiers Nombres probablement premiers
DicoNombre	Nombre 101 Nombre 18 181 Nombre 95 959
Sites	Sur Internet, il existe de nombreux calculateurs de nombres premiers. Celui-ci (en anglais), me semble intéressant; https://www.easycalculation.com/prime-number.php car il donne les deux nombres premiers autour Celui-ci de Math is Fun https://www.mathsisfun.com/prime_numbers.html indique si premier sinon donne la factorisation des nombres successifs (voir cas en bas de page) Prime Number generator and Checker – Number Empire – Pour de grands nombres y compris factorisation et nombres premiers voisins Liste de nombres premiers
Cette page	http://diconombre.fr/aNombre/TYPMULTI/Premier.htm