|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres premiers SOMME des chiffres |
Anglais: Sum of digits of primes
|
|
|
|
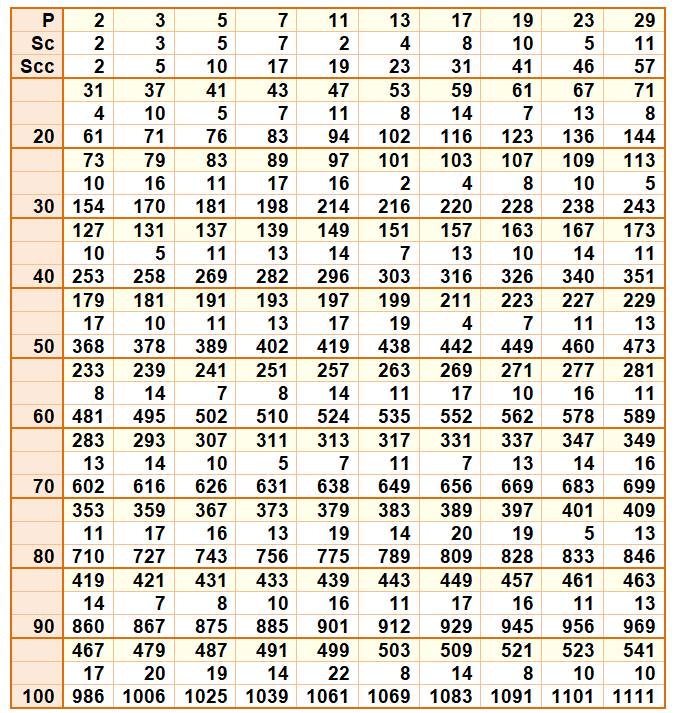
On
sait déjà que la somme des chiffres d'un nombre premier n'est pas
divisible par 3, du fait que les nombre premiers sont en 6k – 1 ou 6k + 1. Sur le tableau qui suit, on donne
la somme (Sc) des chiffres de chaque nombre premier (P) et la somme cumulée
(Scc) de ces sommes individuelles. Lecture: 29 est le dixième nombre premier, la somme des
chiffres est 11 et celle des chiffres de tous les premiers jusqu'à 29 est 57.
Le vingtième est 71, somme 8 et somme cumulée 144
Liste des sommes jusqu'au centième premier: {2, 3, 4, 5, 7, 8, 10, 11,
13, 14, 16, 17, 19, 20, 22} Jusqu'au 10 000e. {… 23, 25, 26,
28, 29, 31, 32, 34, 35, 37, 38, 40, 41, 43, 44} |
|
|
En
moyenne, il y a autant de nombres premiers pour lesquels la somme des
chiffres est paire que ceux pour
lesquels la somme est impaire. Conjecture émise en 1968 par Alexandre Gelfond et prouvée en 2010 par deux chercheurs de
l'Institut de Mathématiques de Luminy (CNRS/Université de la Méditerranée):
par Christian Mauduit et Joël Rivat. Cette propriété sert à la construction de suites de
nombres pseudo-aléatoire, sujet important qui trouve des applications en
simulation numérique et en cryptographie.
>>> |
|
|
||
|
Théorème L'écart entre nombres premiers ayant la même somme de chiffres est un
multiple de 2, de 3, de 6 et de 9. Cette
propriété résulte du fait que:
|
Démonstration (principe avec nombres à deux
chiffres) P1 = 10a + b et P2 = 10c + d P1 – P2 = 10 (a – c) + (b – d) Or, la somme des chiffres est égale: a + b = c + d a – c = d – b En remplaçant: P1 – P2 = 10 (a – c) + (b – d) = 9 (a – c) La différence est divisible par 3. Or, la distance entre premier est en {6H – 2, 6H,
6H + 2}. Seule possibilité de divisibilité par 3: la différence est en 6H. Preuve générale (preuve par 9) P1 mod 9 = SCP1 P2 mod 9 = SCP2 Or, somme des chiffres de P1 = sommes es chiffres de P2. (P1 – P2) mod 9 = 0 La différence est un multiple de 9 et aussi de 3. Si P1 et P2 sont des premiers, leur différence est en {6H – 2, 6H, 6H + 2}. Seule possibilité de divisibilité
par 3: la différence est en 6H. |
|
|
Table des nombres premiers avec une somme donnée
(colonne de gauche) Premiers jusqu'au millième dont la somme vaut de 2 à 10. La deuxième ligne en ocre indique la différence entre deux premiers
successifs. Ex: Avec la somme 2, il ya seulement deux premiers 11 et 101 dont
la différence est 90.
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
![]()