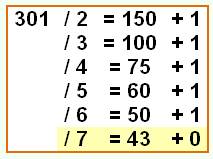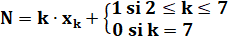|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres avec restes 1 lors de divisions successives
Exemple Le nombre 301 a un reste égal à 1 lorsque
divisé par 2, 3, 4, 5, ou 6. Ce nombre est exceptionnel car il est aussi
divisible par 7. |
|
|
||
|
Énigme: Une dame
se rend au marché pour vendre ses œufs quand un passant la bouscule et les
œufs sont cassés. Voulant
réparer le dommage, le passant demande: combien y avait-il d'œufs ? La dame
répond: je ne sais plus, mais je me souviens qu'en les divisant par 2, 3, 4,
5 ou 6, il en reste toujours un. En les mettant en groupes de 7, je vide
complètement mon panier. Quelle la
plus petite quantité d'œufs ? Anglais: Egg Basket Puzzle |
Solution La clé de la solution est simple: soit N le
nombre d'œufs. Ce nombre est tel que en lui retirant 1, le nouveau nombre est
divisible à la fois par 2, 3, 4, 5 et 6. Le plus petit nombre divisible par 2 et 3 est 6. Finalement, le nombre 60 + 1 = 61 a un reste égal
à 1 quand il est divisé par 2, 3, 4, 5, ou 6. Le nombre 61, n'est pas divisible par 7. Reste à
trouver un multiple de 60 auquel on ajoute 1 qui soit divisible par 7. On
cherche: 61, 121, 181, 241, 301: bingo ! Le nombre 301 est la plus petite solution (voir
illustration dans l'encadré du titre). Toutes les solutions: n = 301 + 420 m. Voir Énigmes
des œufs |
|
Coin
expert
|
Formulation algébrique Sachant que xk est un entier,
minimiser le nombre N. La solution produit les nombres Xk =
{150, 100, 75, 60, 50, 43} |
|
|
Solution générale avec théorie des nombres La solution est telle que: |
|
|
La solution est racine de cette équation |
60x + 7y = 1 => (x, y) = (2, –17) |
|
Ce qui conduit à: |
N = 1 · 7 · (–17) + 0 · 60 ·
2 mod 420 N = –119 mod 420 |
|
Dont la plus petite solution est |
N = 420 – 119 = 301 |
Le nombre
301 en roman


Extrait du roman: La source – James A. Michener – Robert Laffont – 2020 / The Source
– 1965
![]()
|
|
||||||||||||||||||||||||||||||||||||
|
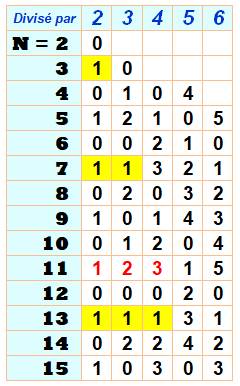
Le nombre
7 est le plus petit nombre qui produit un reste 1 deux fois de suite:
Le nombre
13 est le suivant avec trois fois le reste 1:
Le nombre
61 est le suivant avec quatre fois le reste 1 et même six fois:
|
Table des restes de la division de
N par k
|
|||||||||||||||||||||||||||||||||||
|
Anatomie de ces nombres |
7 = 6 + 1 et 6 est divisible par 2 et 3. 13 = 12 + 1 et 12
est divisible par 2, 3 et 4. 61 = 60 + 1 et 160 est divisible par 2, 3, 4 et 5. |
|||||||||||||||||||||||||||||||||||
|
Liste des plus petits nombres avec
reste 1, k fois de suite Les nombres N – 1 sont des super-primorielle:
nombres divisibles par tous les nombres jusqu'à k. Ce sont aussi des nombres hautement
composés nombres totalisant un record de quantité de diviseurs. |
Le nombre 720 720 est divisible par tous les
nombres de 2 à 16. Pour tous ces diviseurs, 720 721 a un reste égal à 1. |
|||||||||||||||||||||||||||||||||||
Voir Nombre
720 720
|
|
|||||||||||||||||||||
|
Quels
sont les nombres, comme 301, qui ont un reste 1 lorsque
divisé par tous les nombres jusqu'à k et divisible par k + 1. Cas de 25 avec k = 4:
Anglais: N is smallest
positive integer multiple of n-th prime, say k*prime(n), such that k*prime(n)
== 1 (mod j) for each integer j with 1 < j < prime(n) – OEIS A094998 |
Exemple 2 248 776 129 601 = 29 x 31 x 18 803 x 133 033 = 28 x 80 313 433 200 + 1 = 27 x 83 288 004 800 + 1 etc. |
||||||||||||||||||||
|
Programme Maple
|
But Lister les nombres de plus en plus grands avec
restes 1 jusqu'à k et divisibles par k + 1. Commentaires La variable k témoignant du record est
initialisée à 2. Boucle d'analyse des nombres n successifs. Création de la liste des restes des divisions par
les nombres successifs jusqu'à 20. La variable kt sert à compter les restes
successifs égaux à 1. Si le reste est différent de 1, arrêt de la boucle de
comptage (break). Si la quantité de restes à 1 (kt) est supérieure
au record précédent (k), test si le nombre est aussi divisible par k + 1 (ici
du fait de la boucle: i + 1). Si positif, impression du nombre et du compte de
restes à 1.
|
||||||||||||||||||||
Voir Nombre 25 / Nombre
25 200
Voir Programmation – Index
|
|
|||
|
Approche Le nombre
11 a pour reste 1, 2, 3 lorsque divisé par 2, 3, 4. Le nombre
10 a pour reste 0, 1, 2 lorsque divisé par ces mêmes nombres. Un nombre
en 0,1, 2, … est suivi d'un nombre en 1, 2, 3, … On
cherche les plus petits nombres ayant de plus en plus des restes en 0, 1, 2,
3, … Les solutions à |
Table des restes de la division de
N par k
|
||
|
Records Après 10 (q = 3 restes successifs à partir de 0),
on trouve 58 avec 5 restes successifs. On note: 58, 5, [0, 1, 2, 3, 4]. Voir liste
ci-contre Ce sont les nombres à restes
unités diminués de 3. Ou encore, le PPCM
(2, 3, 4, 5, ..) diminué de 2. |
10, 3, [0, 1, 2] 58, 5, [0, 1, 2, 3, 4] 418, 6, [0, 1, 2, 3, 4, 5] 838, 7, [0, 1, 2, 3, 4, 5, 6] 2 518,
9, [0, 1, 2, 3, 4, 5, 6, 7, 8] 27 718, 11, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 360 358, 14, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13] 720 718, 15, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14] |
||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
![]()