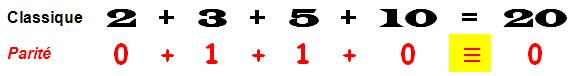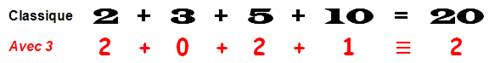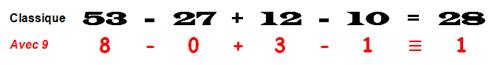|
||||||||||||||||||||||||||||||||||||
![]()
|
PARITÉ Une façon très particulière de
compter: C'est la preuve par neuf des ordinateurs.
|
|
|
|
|
Observation
Conclusion
Exemple
|
|
|
|
|
|
Principe
En
réalité
|
|
|
|
|
|
En rouge, les restes de la division par 3 de
chacun des nombres de l'addition. La somme vaut 5 et le reste de la division
de 5 par 3 est 2. Avec l'addition classique, la somme est 20 dont la division
par 3 donne un reste de 2 (car 20 = 3 x 6 + 2).
Toujours bon! Le reste de la division de 20 par 5
est bien nul.
Oui! C'est la classique preuve par neuf.
Son intérêt sur les autres est double:
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()