|
|||||||||||||||||||||||||||||||||||
![]()
|
Primalité & Factorisation des nombres Deux problèmes successifs:
Trouver les
facteurs d'un nombre est utile en général, mais a regagné de l'intérêt ces
dernières décennies du fait que les codes de
sécurité des échanges informatiques
sont basés sur la grande difficulté (impossibilité) de factoriser de très
grands nombres. |
Trouver les facteurs d'un nombre
|
Sur ces pages Pour les facteurs des nombres de 1 à 1000 >>> Pour les nombres premiers de 1 à 10 000 >>> Pour une majorité des nombres: factorisation et propriétés >>> Sur Internet Tapez isprime (votre nombre) dans un moteur de recherche et vous aurez le choix. Calculateur
en ligne: Entrez votre nombre et choisissez la fonction find the prime factorisation dans le menu déroulant. |
Gauss (1801)
|
The problem of distinguishing prime numbers from composite
numbers and of resolving the latter into their prime
factors is known to be one of the most important and useful in
arithmetic. C.F.
Gauss – 1801 - Disquisitiones Arithmeticae |
|
|
|
|
Avant les machines Au XVIIe siècle: table des facteurs des nombres jusqu'à
24000. 1668:
tous jusqu'à 100 000. Au XVIIe siècle: tous jusqu'à 10 000 000 par Johann
Dase (1824-1861) Au XIXe siècle: 100 000 000 par J.P. Kulik (Prague)
avec quelques erreurs. Au-delà, ces tables ne tiennent plus sur du papier. Avec les machines Un des premiers grands nombres factorisés
par machine (Lehmer): 293
+ 1 = 9 903 520 314 283 042 199
192 993 793 = 0,99… 1028 = 6 442 450 947 x 1 537 228
672 093 301 419 = 6 442 450 947 x 529 510 939
x 2 903 110 321 1971: factorisation d'un nombre "difficile" de 40 chiffres. 1982: Supercalculateur (Cray 1)
craque les 50 chiffres. 1988: Facteur k
trouvé en 1988 par coopération de centaines d'ordinateurs. k = 11104
+ 1 / 118 + 1. La limite des 100
chiffres est atteinte. Pour se trouver en zone
sûre, le codage en cryptographie adopte
des nombres à 200 chiffres. 2010: Factorisation du RSA 768 >>> |
|
D'après: Dites un chiffre de Malcom Lines -
Flammarion
|
|
||
|
|
111 n'est pas premier,
la somme de ses chiffres est égale à 3 ce qui indique qu'il est divisible par
3 et donc pas premier; Avec une petite
division, on trouve l'autre facteur: 111 = 3 x 37. |
|
|
|
||||||
|
|
La recherche de
divisibilité est assez facile pour les nombres 2, 3, 5 et 11 (et leurs multiples). 456 = 2 x 228 453 = 3 x 151 455 = 5 x 91 459 = 9 x 51 450 = 10 x 45 451 = 11 x 41 Ayant épuisé ces
possibilités, il faut recourir à la division classique:
|
|||||
|
|
||
|
|
Un nombre est
divisible par n si le reste de sa division par n est nul. Un nombre divisé par 7
donne les restes 0, 1, 2,3 ,4 5 et 6; seul le reste 0 montre que le nombre
est divisible par 7. Minuit et midi sont
des horaires multiples de 12. Le calcul de l'horloge fait que 14h devient 2h.
On a retiré 12heures. 14 2 est congru à 14
modulo 12 Ce qui veut dire que,
dans le monde du 12, 2 et 14 sont équivalents. 9 + 5 = 14 11 + 12 = 23 12 + 12 = 24 13 + 12 = 25 9
x 4 = 36 9 x 5 = 45 |
|
|
|
109 824 109 825 109 826 Ce dernier nombre est
composé: 109 826 = 89 x 1234. |
|
|
|
||
|
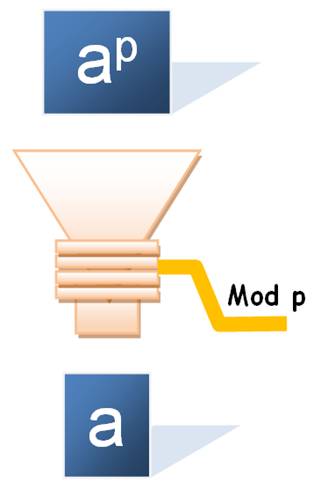
a puissance p est égal à a
modulo p. Exemples
(Le reste de 32
divisé par 5 est 2)
|
Tout nombre a, déguisé en puissance p,
se faisant happer par la machine à modulo p, sera haché menu pour
recracher tout ce qu'il a. |
|
Voir suite et exemples
en Modulo / Divisibilité par 11
|
En
2002, Manindra Agrawal (Kapur,
Inde), Neeraj Kayal et Nitin Saxena (AKS), annoncent avoir trouvé un test de
primalité rapide dérivant du petit théorème de Fermat. Agrawal résume sa
découverte par "Les premiers sont en P". Ce qui veut dire que la temps
de calcul de la primalité est, en gros, proportionnel à sa quantité de
chiffres. C'est,
rapide mais encore assez pour déjouer les systèmes
de cryptage. |
|
|
||
|
|
(n – 1)!
+ 1 est divisible par n, seulement si n est premier. Pour n = 5: 4! + 1 =
25, divisible par 5 |
|
Voir suite et exemples en Théorème de Wilson
|
|
||
|
|
24 – 1 = 15 =3 x 5 25 – 1 = 31 premier 26 – 1 = 63 = 3 x 3 x 7 27 – 1 = 127 premier etc. |
|
Voir Primalité des nombres de Mersenne
|
|
|
|
Voir page spéciale >>> Ce test a été amélioré par Maurice Kraitchik en utilisant les modulos des carrés. |
|
|
|
|
|
De nombreux algorithmes ont été développés. Cela dépasse le cadre de ce
site. La factorisation est d'autant plus difficile que les facteurs sont de
tailles voisines. |
|
|
|
|||
|
Selon ce que l'on cherche |
Premier ou composé? |
Facteurs |
|
|
Tout nombre |
·
Critères de
divisibilité ·
Congruences (modulos)
|
·
Crible d'Ératosthène ·
Méthode de Fermat |
|
|
Nombres spécifiques |
·
Mersenne (2n – 1)
|
·
Nombres divisibles
d'après un critère de divisibilité. |
|
![]()
|
Index |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()