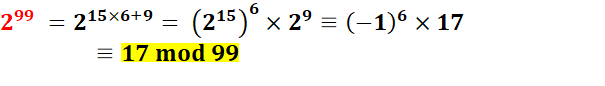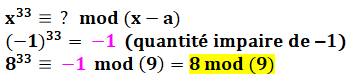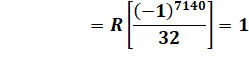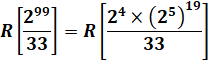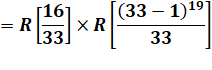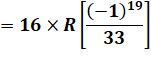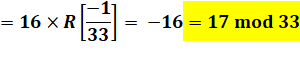NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Arithmétique
Débutants Opérations	MODULO					Glossaire Nombres
INDEX Théorie des nombres	Introduction	Théorie		Propriétés	Formulaire
	Applications	Calculs		Carrés	Cubes
	Jeux	Sun Zi		Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7		Log Modulaire	11^10 = 32 mod 71
	Classes de congruence		Cas de 2^33 et 2^99		Magie
	Terminale S et +	Sommaire de cette page Restes de 2^99 divisé: >>> par 9 – Théorème du reste >>> par 33 – Décomposition-puissance >>> par 33 – Méthode puissances de 2 >>> par 33 – Méthode restes chinois >>> par 99 – Méthode restes chinois >>> par 33 – Méthode générale du totient >>> par 33 – Méthode binomiale

Méthodes de calcul des CONGRUENCES

Exemples avec 2⁹⁹ mod 33 et mod 99

Mise en évidence de plusieurs méthodes (avancées) du calcul des congruences:

Théorème des restes;

Décomposition binaire;

Restes chinois;

Totient d'Euler; et

Méthode binomiale.

Autour de 2⁹⁹

2^99 = 633 825 300 114 114 700 748 351 602 688 = 0,633 … 10^30 (trente chiffres)
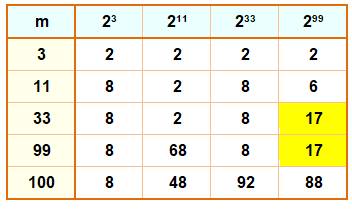
Table des puissances de 2 modulo m Notez que: 2^99 ≡ 17 mod 33 2^99 ≡ 17 mod 99

Puissances de 2 mod 99 (exemple: 2³⁰ ≡ 1 mod 99

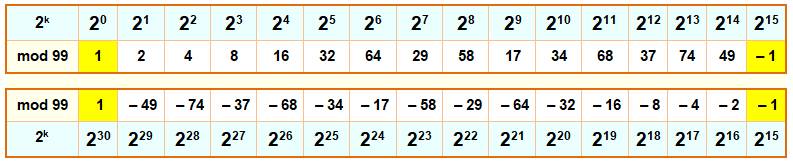
Reste de 2⁹⁹ divisé par 99 avec lecture de la table ci-dessus

Notez la coïncidence: 99 = 3 x 3 x 11 et 3 + 3 + 11 = 17

Reste de 2^99 divisé par 9 – Théorème du reste
Théorème du reste Si un polynôme f(x) est divisé par une expression du type (x – a), le reste est le même que celui de f(a).	Ex: (x² – 4x + 2) / (x – 3) Reste avec a = 3: 3² – 4x3 + 2 = – 1 En effet: (x² – 4x + 2) = (x – 3)(x-1) – 1
Un logiciel de calcul donne le résultat. Mais comment calculer cette valeur ?
Pour appliquer le théorème du reste, il faut trouver x – a = 9. Avec les puissances de 2, on peut avoir x = 2^3 = 8 et 8 – (–1) = 9. Soit : a = –1.	Calculons: 2^99 = 2^3 x 33 = (2^2)^33 = 8^33 Il faut donc calculer:
Application du théorème avec x = 8 et a = –1 alors que f(x) = x^33

Reste de 2^99 divisé par 33 – Décomposition-puissance
On remarque que 2^5 = 32, proche de 33.	2^99 = (2^5)^19 x 2^4
Avec 2^5 ≡ –1 mod 33:

Reste de 2^99 divisé par 33 – Méthode Puissances de 2
Un logiciel de calcul donne 17, mais comment le calculer ?
Expression de la puissance et somme de puissances de type binaire avec: 99 = 64 + 32 + 4 + 1 => 9910 = 11000112
Établissement de la table en mod 33 Il nous faut 1, 2 , 32 et 64. Chaque étape profite des calculs précédents. Il est ainsi facile de doubler en prenant le carré. On n'hésite pas à prendre les valeurs négatives pour conserver les plus petits nombres.
Retour à notre nombre en mod 33

Reste de 2^99 divisé par 33 – Méthode restes chinois
33 = 3 x 11
En mod 3, avec 4 ≡ 1 mod 3:
En mod 11, avec 2^10 = 1 024 ≡ 1 mod 11 En effet 1 023 = 11 x 93. Ou preuve par 11 (1+2 = 0+4).
Inverse modulaire de 2 mod 11 = 6.
En mod 11:
Application simple du théorème des restes chinois en examinant les deux listes mod 2 et 11 et en constant un élément commun.
Soit la solution:

Reste de 2^99 divisé par 99 – Méthode restes chinois
99 = 9 x 11
En mod 9
En mod 11
Restes chinois
Soit la solution:

Reste de 2^99 divisé par 33 – Méthode générale du totient
Théorème du totient d'Euler Si n et a sont premiers entre eux, alors: Avec phi(n), le totient: quantité de nombres entre 1 et n qui sont premiers avec n. On note que: ϕ(p^k) = (p – 1) ϕ(k^p – 1) P est premier et k un entier positif Et aussi: ϕ(m.n) = ϕ(m). ϕ(n) avec PGCD(m,n) = 1 Voir Propriétés des totients	n = 33 et a = 2 Nombres qui sont bien premiers entre eux (coprimes) 3 et 11 étant premiers, tous les nombres inférieurs sont premiers avec eux.
Avec le plus petit multiple de 20:
En modulo 33:
Quelle est la valeur de 1 / (2 mod 33) ? Inverse modulaire de 2 mod 33.	C'est un nombre u tel que 2.u ≡ 1 mod 33 La solution est 17 avec 34 ≡ 1 mod 33
Valeur du reste (résidu) cherché:

Reste de 5^99 divisé par 33 Méthode générale. Exemple avec la puissance de 5:
Reste de 2^97 divisé par 33

Reste de 2^99 divisé par 33 – Méthode binomiale
Théorème du binôme Dans le développement du binôme (a + b)^n tous les termes sont divisibles par a, sauf le dernier. Si on divise ce binôme par a, le reste est le dernier terme. De même en divisant par a², le reste est constitué des deux derniers termes.	Exemple: (a + 2b)^3 = a^3 + 6a^2b + 12ab^2 + 8b^3 Reste la division par a = 8b^3 (a + 2)^10 = a^10 + … Reste la division par a = 2^10 = 1024
Cas où cette méthode est efficace On note R[n / d] le reste de la division de n par d. Dans l'exemple: on note que 96 est divisible par 32. D'où la simplification.
Pour notre cas Avec 99 = 5 x 19 + 4

Suite	Autres exemples de calcul Problème de Sun Zi – Autre exemple de calculs Puissances de 2 mod 641
Voir	Jeux – Index Équations Divisibilité Clé de divisibilité, une application de la théorie du modulo La division Exemple d'application du modulo en Codage RSA Nombres pseudo-premiers
Aussi	Calcul mental Géométrie Nombres Premiers Nombres Rationnels Preuve par 9 – Glossaire Théorie des nombres Variations sur les carrés
Sites	What's the reminder when 2^99 is divided by 33 ? - Quora Binomial theorem – Quora https://www.quora.com/Whats-the-remainder-when-2-99-is-divided-by-33
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Mod3m99.htm