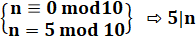NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/05/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Arithmétique
Débutants Opérations	MODULAIRE				Glossaire Nombres
INDEX Théorie des nombres	Introduction	Théorie		Propriétés	Formulaire
	Applications	Calculs		Carrés	Cubes
	Jeux	Sun Zi		Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7		Log modulaire	11^10 = 32 mod 71
	Classes de congruence		Cas de 2^33 et 2^99		Magie
	N = 1 mod k (k = 2, 3,…)
	Terminale S	Sommaire de cette page >>> Équation en modulo >>> Divisibilité par 5 >>> Carré >>> Exemple de mise en bouche >>> Intérêt du modulo >>> Preuves Et Modulo >>> Modulo & Fermat >>> Calcul multi-modulo

Arithmétique modulaire

Applications

Intérêt de cette arithmétique basée sur les restes aux problèmes de divisibilité. Autres applications.

Équation en modulo
Le calcul modulo offre bien des avantages, mais résoudre des équations dans ce mode nécessite une bonne intuition ou une grande pratique. Ici, ajouter du 13 pour réussir à mettre en évidence un carré

Divisibilité par 5 – Exemple simple
Démontrer que si n est égal à 0 ou 5 mod 10 alors n est divisible par 5.
On se souvient que, par exemple: 73 3 mod 10 veut dire: C'est une manière d'écrire la division euclidienne en ignorant le quotient (ici 7 = k).	73 = 10 x 7 + 3 73 = 10 x k + 3
n égal 0 mod 10 est un raccourci pour dire: n égal 5 mod 10 est un raccourci pour dire:	n = 10k = 5 x 2k n = 10k + 5 = 5 (2k + 1)
Que l'on soit dans le premier cas ou le second:	n est divisible par 5

Voir Divisibilité par 5

Carré – Exemple simple

Soit , prouver:

Les exemples du tableau semblent confirmer la propriété: un carré divisé par 4 produit un reste nul ou unité; jamais 2 ou 3.

Un nombre comme 1234 = 308 x 4 + 2 ne peut pas être un carré. 1236 = 309 x 4 pourrait l'être, mais ne l'est pas. En revanche, 1296 = 324 x 4 est un bon candidat et 1296 = 36².

n	n²	mod4
0	0	0
1	1	1
2	4	0
3	9	1
4	16	0
5	25	1

Cas des nombres pairs

Alors n = 2k, le carré est divisible par 4.

Cas des nombres impairs

Alors n = 2k+1, le carré est un multiple de 4 plus 1.

Voir Carrés divisés par 2 et par 4 / Somme de carrés

Exemple pour mise en bouche
Voici un exemple tout simple qui va servir dans des démonstrations plus compliquées. Est-ce que l'expression E = 3s² + q² est divisible par 3, sachant que q ne l'est pas? Non, cette expression n'est pas divisible. D'ailleurs, c'eût été la même chose sans les carrés!	3s² 0 mod 3 3s² + q² q² mod 3 q² mod 3 3s² + q² q² mod 3 3s 0 mod 3 3s + q q mod 3 q mod 3 3s + q q mod 3

INTÉRÊT DU MODULO Démonstration de divisibilité
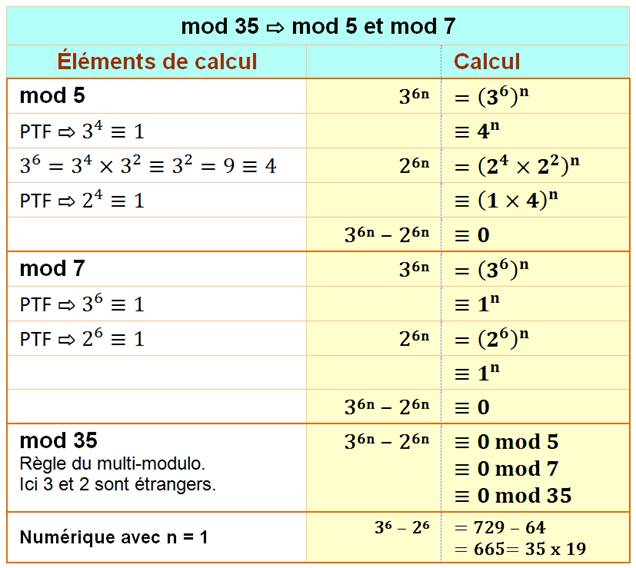
Démontrer que	2047 = 2^11 – 1 est divisible par 23
Commençons avec	2^5 = 32
Avec modulo 23	2^5 = 32 9 mod 23
En élevant au carré	2^10 9² mod 23 81 mod 23 12 mod 23
En multipliant par 2	2 . 2^10 2 . 12 mod 23 2^11 1 mod 23
Enfin, en retirant 1	2^11 – 1 1- 1 mod 23
Résultat final	2^11 – 1 0 mod 23
Nombre parfait ? 2^10 (2^11 - 1) n'est donc pas un nombre parfait. Car le deuxième terme n'est pas premier. Voir Formule d'Euclide

PREUVES ET MODULO – Cas du modulo 8
Pour tout nombre impair x	x {1 , 3 , 5 , 7} mod 8
Son carré	x² {1² , 3² , 5² , 7²} mod 8
Calculons	x² {1 , 9 , 25 , 49} mod 8 {1 , 1 , 1 , 1} mod 8
Ah! surprise	x² 1 mod 8 avec x impair
Conclusion Le carré d'un nombre impair est un multiple de 8 plus 1 Exemple : 13² = 169 = 21 x 8 + 1

MODULO & FERMAT

CARRÉ en MODULO 2

Un nombre x divisé par 2 donne soit 0 soit 1 comme reste.

Son carré donne les mêmes restes au carré.

Il se trouve que ce sont les mêmes valeurs.

D'où la propriété:

x² et x ont mêmes restes lorsqu'ils sont divisés par 2.

x garde sa parité

lorsqu'il est élevé au carré.

	Cas 1	Cas 2
x	0	1
x²	0² = 0	1² = 1
x^2 x mod 2

Exemple

4² 4 mod 2

16 = 2 x 6 + 4

CUBES en MODULO 3

Même type de commentaire.

x³ et x ont mêmes restes lorsqu'ils sont divisés par 3.

	Cas 1	Cas 2	Cas 3
x	-1	0	1
x^3	(-1)^3 = -1	0^3 = 0	1^3 = 1
x^3 x mod 3

Exemple

4³ 4 mod 3

64 = 2 x 30 + 4

Puissance 4 en MODULO 4

Même type de commentaire.

x⁴ et x n'ont pas mêmes restes lorsqu'ils sont divisés par 4.

	Cas 1	Cas 2	Cas 3	Cas 4
x	x	-1	0	1
x^4	x^4	(-1)^4 = 1	0^4 = 0	1^4 = 1
x^4 n'est pas x mod 4

Puissance 5 en MODULO 5

Même type de commentaire.

x⁵ et x ont mêmes restes lorsqu'ils sont divisés par 5.

	Cas 1	Cas 2	Cas 3	Cas 4	Cas 5
x	-2	-1	0	1	2
x^5	(-2)^5 = -2	(-1)^5 = -1	0^5 = 0	1^5 = 1	2^5 = 2
x^5 x mod 5

Exemple

4⁵ 4 mod 5

1 024 = 5 x 204 + 4

PUISSANCE p en MODULO p

On aura compris que le truc: ça ne marche qu'avec les nombres premiers. Et on aura en effet, comme l'a trouvé Fermat:

Petit théorème de Fermat

x^p º x mod p

p étant un nombre premier.

Ou, autre formulation:

x ^p et x ont mêmes restes lorsqu'ils sont

divisés par p.

Voir Démonstration / Fermat

Calcul multi-modulo
Outils nécessaires Nombres premiers entre eux (ou étrangers), Petit théorème de Fermat (PTF): x^p-1 1 mod p (x et p étrangers), Propriété (règle) des multi-modulos. Montrez que 35 divise toujours 3^6n – 2^6n.

Voir Divisibilité

Suite	Modulo et jeux Petit théorème de Fermat – Calculs
Voir	Clé de divisibilité, une application de la théorie du modulo La division
Aussi	Calcul mental Clé de divisibilité Divisibilité par 11 Géométrie Nombres Cycliques Nombres Rationnels Preuve par 9 – Glossaire Preuve par 9 – Débutant Théorie des nombres
Diconombre	Nombre 2 Nombre 3 Nombre 4

Référence de cette page

Arithmétique modulaire et ses applications http://villemin.gerard.free.fr/Wwwgvmm/Nombre/ModAppli.htm