|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre multiple de son retourné PALINTIPLE Nombre retourné divisible Nombre/ Retourné = Entier Ils
ne sont que deux et engendrent une famille infinie. Ce sujet est également traité en Nombres
retournée en proportions.
|
Anglais: palintiple: an integer multiple of
its digital digit reversal / reverse multiples /
palindromic multiple /
reverse-divisible number
|
Quel
nombre de quatre chiffres se retourne
lorsque multiplié par 4 ? What 4-digit number reverses
its digits when multiplied by4 ?
|
Sérieux?
|
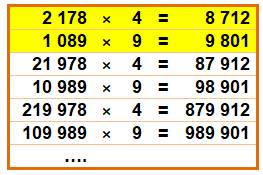
"Les
nombres 8 712 et 9 801 sont les deux seuls nombres à quatre chiffres qui
sont multiples
de leur retourné". Citation de G. H. Hardy
qui donnait un exemple de mathématiques récréatives mais futiles. Pourtant
les mathématiciens ont formalisé et étudié ce concept en base décimale. En
1966, Sutcliffe généralise à une base quelconque. Kaczynski cherche les
solutions pour 2 et 3 chiffres et montre qu'elles sont liées. Lara Pudwell s'attaque à 4 et 5
chiffres. Hardy states:
8712 and 9801 are the only four figure numbers which are integral multiples
of their reversals"; and, he further
comments that "this is
not a serious theorem,
as it is
not capable of any significant generalization." |
|
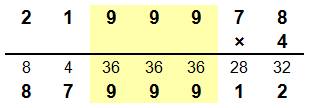
2178 x 4 =
8712 Explications (1000A + 100B + 10C + D) x 4 = 1000D + 100C + 10
B + A 4000A + 400B + 40C + 4D = 1000D + 100C + 10 B + A Les deux nombres sont pair (4D pour les unités);
A est pair. 4000A ne doit pas dépasser 9999 (quatre
chiffres); A = 2. 2BCD x 4 = DCB2 Avec les milliers en 2 x 4, DCB2 est supérieur à
8000; D = 8 ou 9. Si D = 9,
alors 4D = 36 et l'unité n'est pas 2; D = 8. 2BC8 x 4 = 8CB2 8000 + 400B + 40C + 32 = 8000 + 100C + 10 B + 2 390B + 30 = 60C 13B + 1 = 2C Seule possibilité: B = 1 et C = 7. |
|
|
||
|
Les deux nombres pilotes Un
palintiple est un nombre qui est égal à k fois son retourné avec k > 1. Le plus
petit non trivial est 8712 dont le retourné 2178 vaut un quart de 8712. Sont éliminés tous les cas triviaux:
|
Notez
que 2 178 =
2 x 1 089 |
|
|
Pourquoi un motif sans fin La multiplication
posée explique la chose. Le motif central se répétée sans fin. |
|
|
Voir Nombre
1089 et magie
|
|
||
|
Chaque
nombre pilotes donne naissances à une suite infinies de palintiples en
intercalant des 9. Une
nouvelle suite est obtenue en concaténant 1, 2, … n nombres pilotes On peut y
intercaler les 9 comme sur le palintiple simple ou encore intercaler des 0
aux points de concaténation. |
|
|
|
|
||
|
|
Commentaires La programmation permet de s'assurer qu'il n'y a
pas d'autres palintiple que les deux pilotes: 8712 et 9801. Réinitialisation avec restart. Boucle de n = 1 à 10 000 Si le nombre n n'est pas un multiple de 10,alors
… Convertir le nombre n en une liste N contenant
les chiffres séparément (attention, ils sont en ordre inverse) Avec n, on compte la quantité de chiffres dans n. Initialisation du nombre r, le retourné de n. Calcul de r en ajoutant les chiffres multipliés
par la puissance de 10 correspondant à leur rang. Calcul du rappor Q entre le nombre et son
retourné. Si ce quotient est entier et différent de 1
(élimination des palindromes), alors imprimer le nombre, son retourné et le
quotient des deux. Fin des
conditions et de la boucle En bleu, résultat du déroulement du programme. |
|
Voir
Calcul rapide du retourné
/ Programmation
– Index
|
Motifs présentés par
W.W.Rouse Ball en 1914.
Mathematical recreations and
essays – pdf 534 pages |
![]()
Devinette
|
Trouvez
un nombre de deux chiffres tel que d'en le retournant il vaut la moitié moins
un de l'original. |
|
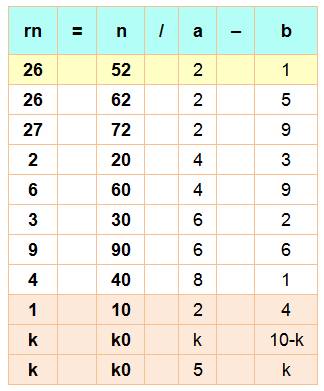
Question Trouvez
un nombre de deux chiffres (n) tel que d'en le retournant (rn) il vaut la
moitié moins un de l'original. Réponse On
a: rn = n/2 – 1 et la seule solution est 52
car 25 = 52 / 2 – 1. Recherche
|
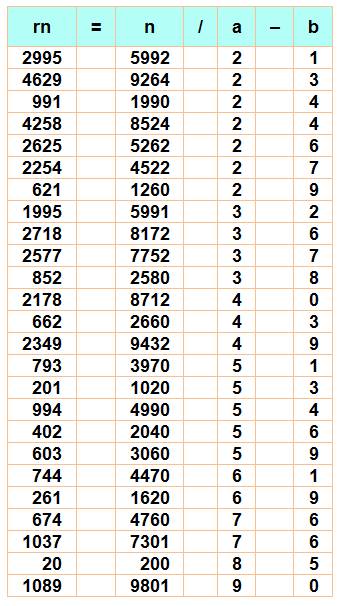
Autres cas à deux chiffres:
rn
= n/a – b
En
bas le cas des dizaines et leur forme générique selon la valeur de la dizaine
k. |
|
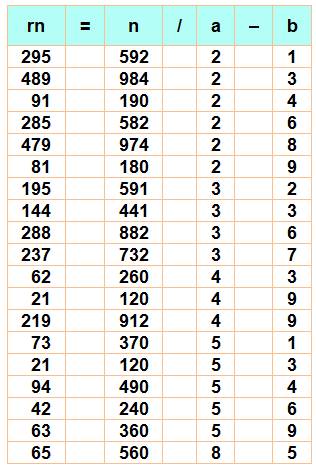
Avec
trois chiffres
|
Avec
quatre chiffres
|
|
Mention
spéciale pour la forme en 25 / 52 25
= 52 / 2 – 1 295
= 592 / 2 – 1 2995
= 5992 / 2 – 1 29…95 = 59..92 / 2 – 1 |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette
page |
![]()