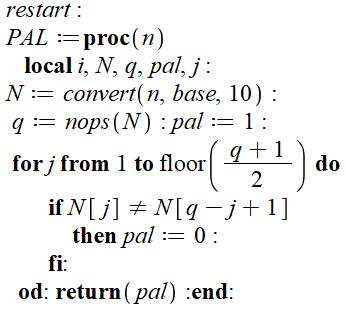NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 20/12/2018

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique         Brèves de Maths

 

Nombres PREMIERS

 

Débutants

Nombres

Premiers

FORMES

 

Glossaire

Nombres

Premiers

 

INDEX

 

Nombres premiers

 

 

 

 

Palindrome

Résistant

Circulaire

Primeval

Minimal

Pyramide

Somme chiffres

 

Sommaire de cette page

>>> Premiers palindromes

>>> Palindromes premiers à 2 chiffres

>>> Palindromes premiers à 3 chiffres

>>> Palindromes premiers à 4 chiffres

>>> Palindromes premiers à 5 chiffres

>>> Palindromes premiers à 7 chiffres

>>> Palindromes premiers à 9 chiffres

>>> Composés palindromes à facteurs palindromes

>>> Curiosité de la bête

>>> Palindromes concaténés premiers

>>> Somme de premiers palindromes

>>> Somme de puissances de premiers

>>> Doublement, triplement palindrome

 

 

 

 

 

Nombres premiers PALINDROMES

 

Les premiers qui se mirent en miroir.

15 à 3 chiffres; 0 à quatre chiffres; 93 à 5 chiffres; 668 à 7 chiffres …

Aucun palindrome premier avec quantité de chiffres pair >>>

 

 

 

PREMIERS PALINDROMES – Introduction

 

Définition

*    Les premiers palindromes sont des nombres premiers qui se lisent aussi bien de gauche à droite que de droite à gauche.

 

Exemples

11

101

10301

…

 

Problème

*    On cherche ces nombres premiers, et leur population selon la quantité de chiffres.

 

Propriété

11

est le seul a avoir

un nombre de chiffres pair

 

 

 PALINDROMES PREMIERS à 2 chiffres

 

*    Seul 11 est premier.

Les autres sont multiples de 11.

*    Seul palindrome premier à nombres pair de chiffres

 

11

22 = 2 x 11

33 = 3 x 11

…

 

PALINDROMES PREMIERS à 3 chiffres

 

*      Il y a 15 palindromes premiers à 3 chiffres.

 

*      Évidemment, aucun ne commence par 2, 4, 6, 8 et 5, car il se terminerait aussi par le même chiffre et, ne serait donc pas premier.

 

 

101

131

151

181

191

313

353

373

383

 

727

757

787

797

 

919

929

 

 

 

*      Curiosité avec 4 palindromes

101 + 131 + 151 = 383

 

 

Cas de 313

 

*      Le nombre 313 est palindrome premier.

Sa valeur binaire: 1001110012

 

*      C'est seul* nombre premier inférieur à, au moins, un 100 millions qui est à la fois palindrome en base 10 et en binaire.

 

* hors cas triviaux: 3 = 112 ; 5 =1012 ; et 7 = 1112 .

Noté par Antoine Traqui dans son roman Point Zéro – 2013 – Pocket 

 

 

 

Les palindromes premiers à trois chiffres

Pour alléger la liste, on a retiré du tableau les nombres terminés par un chiffre pair et par 5 qui sont de toute manière composés.

101

Premier

707

7 x 101

111

3 x 37

717

3 x 239

121

11²

727

Premier

131

Premier

737

11 x 67

141

 3 x 47

747

3² x 83

151

Premier

757

Premier

161

7 x 23

767

13 x 59

171

3² x 19

777

3 x 7 x 37

181

Premier

787

Premier

191

Premier

797

Premier

303

 3 x 101

909

 3² x 101

313

Premier

919

Premier

323

17 x 19

929

Premier

333

3² x 37

939

3 x 313

343

73

949

13 x 73

353

Premier

959

7 x 137

363

 3 x 11²

969

3 x 17 x 19

373

Premier

979

11 x 89

383

Premier

989

23 x 43

393

3 x 131

999

33 x 37

 

 

  

PALINDROMES PREMIERS à 4 chiffres

 

*      Il n'en n'existe aucun.

*      La division par 11 de ces palindromes produit souvent un palindrome:

*            45 sur 90 à quatre chiffres;

*          330 sur 900 à six chiffres;

*       2 145 sur 9000 à huit chiffres;

*       etc.

 

Tous les nombres palindromes à nombre de chiffre pair sont divisibles par 11.

 

Exemples

    1221 = 11 x 111

    8998 = 11 x 818

123321 = 11 x 11211

99799799 = 11 x 9072709

 

 

 

  PALINDROMES PREMIERS à 5 chiffres

Il y en a 93

 10301

10501

10601

11311

11411

12421

12721

12821

13331

13831

13931

14341

14741

15451

15551

16061

16361

16561

16661

17471

17971

18181

18481

19391

19891

19991

30103

30203

30403

30703

30803

31013

31513

32323

32423

33533

34543

34843

35053

35153

35353

35753

36263

36563

37273

37573

38083

38183

38783

39293

70207

70507

70607

71317

71917

72227

72727

73037

73237

73637

74047

74747

75557

76367

76667

77377

77477

77977

78487

78787

78887

79397

79697

79997

90709

91019

93139

93239

93739

94049

94349

94649

94849

94949

95959

96269

96469

96769

97379

97579

97879

98389

98689

 

 

 

 

 

PALINDROMES PREMIERS à 7 chiffres

 

*      Il existe 668 palindromes premiers de 7 chiffres.

 

Exemples ci-contre =>

 

abbbbba

 

1333331

1444441

1777771

3222223

3444443

7666667

9222229

9888889

aaabaaa

 

1114111

1117111

3331333

3337333

7772777

7774777

7778777

Formes particulières

*      En creux: =>

Seul représentant

 

*      En bosse =>
Aucun représentant

 

*      En bosse avec centre libre =>
Aucun représentant

 

 

a (a – 1) (a – 2) (a – 3) ...

7654567

 

a (a + 1) (a + 2) (a + 3) ...

 

 

a (a – 1) (a – 2) b ...

3212123

*      Seul cas de ce motif =>

 

1 878 781  1 879 781 

1 880 881  1 881 881

 

 

 

   PALINDROMES PREMIERS à 9 chiffres

 

*      Voici les deux seuls premiers à motif

 

En bosse:                           3456 7 6543

En bosse et centre libre:   3456 5 6543

 

 

 

 

NOMBRES COMPOSÉS PALINDROMES

 à facteurs palindromes

 

*      Plus petit palindrome ayant n facteurs premiers palindromes

 

N

Palindrome

Facteurs premiers palindromes

0

1

-

1

2

2

2

4

2 x 2

3

8

2 x 2 x 2

4

88

2 x 2 x 2 x 11

5

252

2 x 2 x 3 x 3 x 7

6

2772

2 x 2 x 3 x 3 x 7 x 11

7

82728

2 x 2 x 2 x 3 x 3 x 3 x 383

8

2112

2 x 2 x 2 x 2 x 2 x 2 x 3 x 11

9

4224

2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 11

10

8448

2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 11

11

236989632

2 x 2 x 2 x 2 x 2 x 2 x 3 x 11 x 11 x 101 x 101

12

48384

2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 7

13

2977792

2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 727

14

?

?

15

?

?

 

*      Plus petit palindrome avec n facteurs premiers distincts

 

N

Palindrome

Facteurs premiers distincts

0

1

-

1

2

2

2

6

2 x 3

3

66

2 x 3 x 11

4

858

2 x 3 x 11 x 13

5

6006

2 x 3 x 7 x 11 x 13

6

222222

2 x 3 x 7 x 11 x 13 x 37

7

22444422

2 x 3 x 7 x 11 x 13 x 37 x 101

8

244868442

2 x 3 x 7 x 13 x 17 x 23 x 31 x 37

9

6434774346

2 x 3 x 7 x 11 x 13 x 17 x 19 x 31 x 107

10

?

?

11

?

?

12

?

?

13

?

?

 

*      Plus petit palindrome ayant n facteurs premiers palindromes distincts

 

 N

Palindrome

Facteurs premiers palindromes distincts

0

1

-

1

2

2

2

6

2 x 3

3

66

2 x 3 x 11

4

6666

2 x 3 x 11 x 101

5

?

?

6

?

?

7

?

?

 

CURIOSITÉ DE LA BÊTE

*      Somme des 666 premiers palindromes premiers

2 391 951 273

*      Trinité de la bête

23 + 33 + 93 + 13 + 93 + 53 + 13 + 23 + 73 + 33
= 666 + 666 + 666

*      Anniversaire de cette découverte

3 x 666 = 1998

De Geest & G.L. Honaker, Jr

 

Palindromes concaténés premiers

Palin

Palindromes concaténés

Valeur

Type

11

 12345678911

 0,1235… 1011

composé

77

 12345678911223344556677

 0,1235…1023

premier

101

 123456789112233445566778899101

 0,1235… 1030

premier

…

Aucun autre premier jusqu’à 1 00 000.

1122334455667 …

En ignorant les premiers chiffres, en commençant par le premier palindrome (en fait un repunit), seul 11 est premier jusqu'à 1 000 000.

 

101111121 …

En ignorant les chiffres et les repdigits , en commençant par le premier réel palindrome, il y a trois tels premiers jusqu'à 1 000 000:

101

101111

101111121131141151161171 = 0,1011… 1024

101121131141

Cette fois, on reprend le cas précédent en éliminant tous les repdigits. Il y a trois premiers jusqu'à 1 000 000.

101

101121131

101121131141151161171 =  0,1011… 1021

 

__________________________

 

 

Programme de recherche nombres palindromes concaténés premiers

 

PAL est une procédure de reconnaissance d'un nombre palindrome.

Conversion de n en base 10 pour disposer des chiffres de n dans une liste.

Comparaison des chiffres en position symétrique. Fin de test à moitié valeur de la quantité q de chiffres dans n.

La procédure retourne 1 si le nombre est palindrome et 0 sinon.

 

Programme principal

Initialisation du mot concaténé P à 0.

Boucle d'exploration en n.

Suite que si n est palindrome.

Calcul en q de la quantité de chiffres dans n avec un logarithme.

Composition du nouveau nombre P concaténé en adjoignant à l'ancien la quantité de 0 suffisante pour y loger le nouveau palindrome n.  

Impression si ce nombre P est premier.

 

Résultat du traitement en bleu.

Voir Programmation – Index

 

 

Somme de premiers palindromes

 

*    Palindromes, somme de deux premiers consécutifs de 2 à 12 000.

 

 

*    Palindromes, somme de trois premiers consécutifs de 2 à 12 000.

 



*    Palindromes, produit de deux premiers consécutifs de 2 à 12 000.

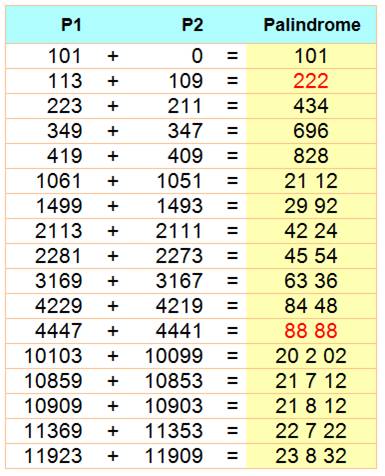
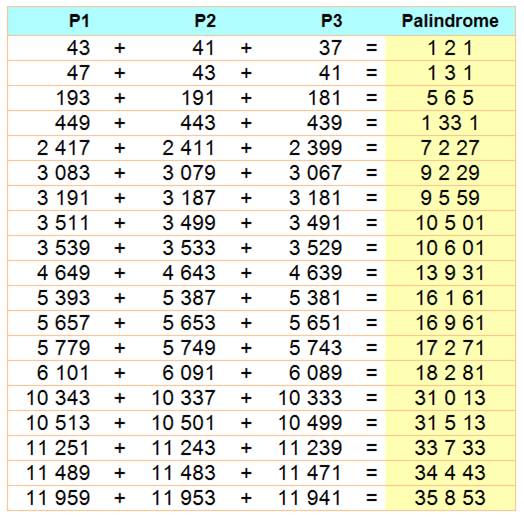
11 x 7 = 77

19 x 17 = 323

193 x 191 =     36 8 63

1061 x 1051 = 111 5 111

 

 

 

Somme de puissances de premiers

 

3 467 643 =   39 + 58 + 77 + 116 + 135 + 174 + 193 + 232 + 291

 

Nombre Palindrome

Somme de nombres premiers successifs, à la puissance de tous les chiffres décroissants.

Carlos Rivera, février 1999, cité par De Geest

 

 

À titre purement indicatif

3 467 643 =

39 + 58 + 77 + 116 + 135 + 174 + 193 + 232 + 291

3 467 614 =

39 + 58 + 77 + 116 + 135 + 174 + 193 + 232

3 467 085 =

39 + 58 + 77 + 116 + 135 + 174 + 193

3 460 226 =

39 + 58 + 77 + 116 + 135 + 174

3 376 705 =

39 + 58 + 77 + 116 + 135

3 005 412 =

39 + 58 + 77 + 116

1 233 851 =

39 + 58 + 77

410 308 =

39 + 58

19 683 =

39

3 467 643 =1 x 3 x 17 x 67 993

 

 

Aussi, dans l'autre sens

 

14 586 375 356 763 =  31 + 52 + 73 + 114 + 135 + 176 + 197 + 238 + 299

  =  1 x 3 x 7 x 694 589 302 703

 

 

Multiplement palindrome

 

Doublement palindrome

Nombres palindromes dont la quantité de chiffres est aussi palindrome.

 

Les plus petits, mais  triviaux: (11, 2), (22, 2) … (101, 3), (111, 3) …

Les plus petits non triviaux: (10000000001, 11), (10000100001, 11) …

 

Doublement palindrome et premiers

(11, 2), (101, 3), (131, 3), (151, 3), 181, 3), (191, 3), (313, 3) …

(10301, 5), 10501, 5), 10601, 5), (11311, 5) …

(1003001, 7), (1008001, 7) …

(10000500001, 11), (10000900001, 11), 10001610001, 11) …

 

Triplement palindrome

(10000000001, 11, 2),  (10000100001, 11, 2) …

(10000000000000000000001, 22, 2) …

 

Triplement palindrome et premiers

(10000500001, 11, 2), (10000900001, 11, 2) ….

Aucun en 22 chiffres, car un palindromes avec une quantité paire de chiffres est toujours divisible par 11.

 

La recherche de ce genre de nombres conduit vite à de très grands nombres. Paulo Ribenboim a réussi à trouver ce très grand triplement palindrome premier:

 

 

 

Voir

*    Nombres premiers – Index

*    Nombres premiers résistants

*    Palindromes premiers

Aussi

*    Palindromes – Dates

*    Palindromes – Mots

*    Palindromes – Nombres

*    Palindromes – Mots et phrases

Site

Pour dossier complet sur les palindromes:

*    Voir site de Patrick De Geest – Site le plus complet sur le sujet

*    Voir répertoire des palindromes premiers
 dans Neil Sloane Integer sequence

*    The record Palindromic Primes – Worldofnumber 

*Propriétés curieuses des nombres palindromes – Gianni Sarcone – Tangente

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Premier/palindro.htm