|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres PALINDROMES CARRÉS Nombres à la fois carrés
et palindromes.
Vous
remarquerez que la racine carrée peut,
elle-même, être un
palindrome, repdigit, premier, triangulaire, carré … (11, 101, 111, 121 …) |
|
|
||||||||||||||
|
Définition Palindrome
carré: palindrome de la forme n², n étant la base ou la
racine. La
base peut aussi être particulière: palindrome, repunit,
carrée, … |
Exemples
|
|||||||||||||
|
Propriétés des palindromes
carrés Voir Unités
des carrés |
Ils se terminent par 1, 4, 5, 6 ou 9. Il existe des séquences infinies de
formation des palindromes carrés (comme pour les cubes,
mais pas pour les triangles). Il n'existe pas de carré palindrome
de longueur: 2, 4, 8, 10, 14, 18, 20, 24 et 30. Il semble que les carrés palindromes
de longueur paire soient peu nombreux. |
|||||||||||||
|
Curiosité palindromique et
carrée |
52 + 92
+ 92 + 52 = 212 et 2122 = 44 944 |
|||||||||||||
Voir DicoNombre
212
|
|
||
|
Programme Maple
Listing pour copie directe dans Maple restart: with(ListTools): Pal := proc (n) local t, N; N := convert(n,
base, 10); t := evalb(N = Reverse(N)); return t end proc: L := []; for n from
10 to 10000 do if Pal(n) = true and type(sqrt(n), integer) then L := [op(L),
[n, sqrt(n)]] end if end do: L; |
Commentaires Réinitialisation générale (restart) et appel des logiciels de traitement de
listes pour disposer de l'instruction Reverse. Procédure Pal
(sous-programme) identifiant les nombres palindromes. Conversion de manière à disposer dans N de la liste des chiffres. Évaluation binaire (evalb)
de l'égalité N avec la liste retournée (Reverse)
de N. La variable t vaut "true"
si l'égalité est satisfaite, c'est-à-dire, si n est un palindrome. Programme principal Ouverture d'une liste L. Analyse des nombres de 10 à 1000. Si le retour de
Palindrome (Pal) est vrai (true) et si la racine carrée (sqrt) de n est un entier (integer) alors ajouter n et sa racine dans la
liste L. op(L) est la liste telle qu'elle
existe déjà. En bleu, le résultat de
la recherche avec le couple: palindrome et sa racine carrée. |
|
Voir Programmation
palindromes carrés (variante sans l'instruction Reverse) / Programmation – Index
|
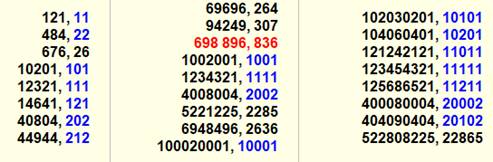
Liste des palindromes carrés
avec leur racine carrée Légende des couleurs 22
=> base palindrome 698 896 => quantité paire de chiffres 676
est le plus petit nombre non palindrome dont le carré est palindrome. |
|
|
|
Les plus grands connus |
n
= 831 775 153 121 251 039 203 514 (24 chiffres) n²
= 691 849 905 349 880 612 384 525 525 483 216 088 943 509 948
196 (48 chiffres, pair). Mike
Bennett janvier 1998 n=
1 373 512 530 649 258 635 292 477 609² n²
= 1 886 536 671 850 530 641 991 373 196 913 731 991 460 350 581 766 356 881 (55 chiffres) Feng Yuan 2008 Source: Palindromic Polygonal
Sporadic Number Record Table – Worldofnumber..com Voir
ce site pour mise à jour |
|
|
Palindrome dont le carré est
palindrome jusqu'à un million |
[11, 121], [22, 484], [101, 10201], [111, 12321], [121,
14641], [202, 40804], [212, 44944], [1001, 1002001], [1111, 1234321], [2002,
4008004], [10001, 100020001], [10101, 102030201], [10201, 104060401], [11011,
121242121], [11111, 123454321], [11211, 125686521], [20002, 400080004],
[20102, 404090404], [100001, 10000200001], [101101, 10221412201], [110011,
12102420121], [111111, 12345654321], [200002, 40000800004] |
|
|
|
||
|
La racine carrée est un
nombre premier Exemple 307 est un nombre
premier et son carré 94 249 est un palindrome. Nombre 101 1012
= 10201 1013
= 1030301 1014
= 104060401 Voir DicoNombre
101 |
121, 11 10201, 101 94249, 307 900075181570009,
30001253 10022212521222001,
100111001 12124434743442121,
110111011 12323244744232321,
111010111 12341234943214321,
111091111 1022321210249420121232201, 1011099011101 1210024420147410244200121, 1100011100011 1210222232227222322220121, 1100101010011 1212223242528252423222121, 1101010101011 10022032324432823442323022001, 100110101011001 10022210341004940014301222001, 100110990111001 10201002020020502002020010201, 101000010000101 10203222143242824234122230201, 101011000110101 10223232102244844220123232201, 101110000011101 |
|
|
Quantité paire de chiffres Ils sont
peu nombreux. Exemple 698 896 est un palindrome de six chiffres
et c'est le carré de 836. |
698 896 David Wells 637 832 238
736 Cédric Brun 4 099 923 883 299 904 6 916 103 777 337
773 016 196 40 460 195 511 188
111 559 106 404 4 872 133 543 202
112 023 453 312 784 9 658 137 819 052
882 509 187 318 569 46 501 623 417 708
833 880 771 432 610 564 1 635 977 102 407
987 117 897 042 017 795 361 Liste OEIS A027829 |
|
|
Racine non palindrome |
|
|||||||||||||||||||||||||||||||||||||||
|
Racine palindrome |
Voir
Suite – Table |
|||||||||||||||||||||||||||||||||||||||
|
Repunits Les repunits commencent bien, mais ne donnent pas une
séquence infinie. |
|
|
Suite de 01 a => Ce N est le plus petit entier qui donne un carré palindrome pannumérique. b
=> Palindrome loupé de 1 seulement. |
|
||||||||||||||||||||||
|
Autres formes de carrés
palindromes Dernier
nombre: non palindrome |
|
Voir Palindromes
en 11, 101, 111 …
|
|
|||||||||||||||||||||||||||
|
Un nombre palindrome quasi carré est de la forme n² + 1. |
Exemples 10² + 1 = 101
25² + 1 = 626 100²
+ 1 = 10001 |
||||||||||||||||||||||||||
|
Propriétés |
Ils se terminent par 1, 2, 5, 6 ou 7. On obtient des séquences infinies avec les 4 formes
suivantes:
On obtient des séquences finies avec les 2 formes
suivantes:
|
||||||||||||||||||||||||||
|
Longueur paire |
Il n'y a pas de tels nombres de longueur paire. Et un nombre de la forme n² + 1 n'est pas
divisible par 11. En effet
On ne trouve jamais 0 sur la 2e ligne: CQFD. |
||||||||||||||||||||||||||
|
Le plus grand connu |
N = 1 009
090 909 090 (13 chiffres). Npqc = 1 018 264 462 808 082 644 628 101 (25
chiffres) Warut
Roonguthai Novembre 1997 |
||||||||||||||||||||||||||
|
Liste des palindromes quasi
carrés |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||
|
Palindromes cubes |
Il
existe beaucoup de palindromes cubes. |
|||||||||||||||||
|
Palindromes bicarrés Tous les
palindromes connus de puissance 4 sont tous à base palindrome et même de la
forme 100..001 avec n zéros (n ³ 0) |
|
|||||||||||||||||
|
Puissance 5 et plus |
Pour les puissances 5 à 10, on n'a pas
trouvé de palindromes. On conjecture qu'il n'y a pas de palindrome
pour nk avec k > 4. |
|||||||||||||||||
![]()
|
Voir |
|
|
Sites |
Voir site de Patrick De Geest
|
|
Cette page |
![]()