|
|||||||||||||||||||||||||||||||
![]()
|
TOURNOIS - Olympiades Comment organiser un tournoi. Un casse-tête.
De nombreux cas, de nombreuses possibilités. Attention, jamais les mêmes
adversaires, mais tous les adversaires … Quelles sont les possibilités? Un tour d'horizon avant de
se lancer à leur résolution.
Des tables (tables
de Berger) récapitulent les cas possibles. Il existe aussi des
logiciels qui aident à la planification de tournois. |
Anglais: Tournament, contest, meeting / Tournament scheduling
|
|
||
|
AB, BA, AC, CA, BC, CB sans tenir compte de
l'ordre: AB, AC, CA.
Q =
½ n(n-1) Il s'agit de la somme des entiers |
Avec trois joueurs, trois matchs: AB, AC, BC. Avec quatre joueurs, six: AB, AC, AD, BC, BD, CD. Avec cinq joueurs, dix matchs: AB, AC, AD, AE
BC, BD, BE
CD, CE DE |
|
|
Le
problème d'organisation des tournois se complique lorsqu'on parle d'équipes
dont chaque joueur d'une équipe doit rencontrer chaque joueur de l'autre et que
… Nous
devons minimiser à la fois le nombre de courts utilisés et le nombre de jours
de matchs. Avec
l'exemple de deux équipes de trois joueurs, il y aura trois matchs par jour
sur trois cours et cela durera trois jours. |
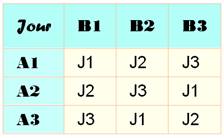
Tennis avec deux équipes de trois joueurs
Ce carré latin
montre l'organisation des matchs
sur trois jours (et trois courts). Trois, car le premier joueur A1 affronte
B1, B2 et B3 en trois matchs successifs (J1, J2 et J3). |
|
|
Encore un
peu plus casse-tête! Comment
organiser la promenade des enfants au cours de l'année de sorte que, en rang
par deux, chaque enfant se retrouve à côte d'un autre à chaque sortie? |
C'est la célèbre énigme de la promenade
des demoiselles posées par Édouard Lucas pour laquelle il propose une
méthode de résolution originale. En anglais: schoolgirls problem |
|
|
De manière basique, on distinguera
trois grands types de tournois:
Le cas du tournoi en double
est résolu avec la méthode Kirkman >>> Le cas de la ronde sociale
n'est résolu que dans certains cas particuliers >>> Dans la réalité, les tournois
présentent d'autres contraintes (comme affronter deux fois ses concurrents).
Des logiciels sur Internet proposent de mettre au point les tournois avec
vous. |
|
|
||
|
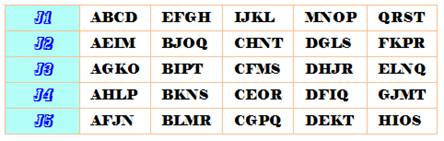
Exemple
de ronde sociale faisable. Vingt golfeurs souhaitent jouer en équipe de
quatre sur cinq jours. Chaque
joueur joue une seule fois contre chacun des autres. |
|
|
Source: Social golfer problem
– Wolfram MathWorld
|
|
||
|
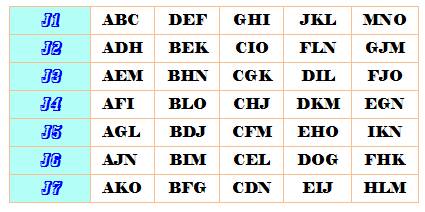
Autre
exemple de ronde sociale faisable. Quinze écolières sortent chaque jour en rang
par trois. Sur la semaine,
aucune des filles ne doit ne retrouver plus d'une fois sur le même rang que
les autres. C'est
aussi le problème de quinze golfeurs jouant par trois. |
|
|
Source: Kirkman's
schoolgirl problem – Wolfram MathWorld
Suite …
|
L'organisation
de rondes sociales est un problème ardu, voir infaisable. Voici
un autre exemple: organisation de repas lors d'un séminaire: 100 convives sur
10 tables de 10. Organiser les tables pour le maximum de repas de façon telle
que les convives ne se retrouvent pas plus d'une fois avec un convive déjà vu
sur sa table. |
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
|
||
|
Cette page |
||
![]()