|
Édition du: 04/12/2023 |
|
INDEX |
GRILLES – Carrés magiques |
||
Faites un double-clic pour un retour en haut de page
![]()
|
TISSUS & Mathématiques
Passer
des fils les uns sur les autres pour constituer un tissu, c'est le tissage. Il
existe trois façons fondamentales pour croiser ces fils: la toile, le sergé
et le satin. Les deux premiers étant des cas particuliers du satin. Le motif
du satin peut être représenté sur une grille carré (un échiquier) appelé
armure. Toutes les permutations
figurées y sont permises (motifs que l'on retrouve dans les carrés
latins). Le
premier à voir théorisé les mathématiques du tissu est Édouard Lucas
(1842-1891), mathématicien français. |
|||
|
|
Sommaire de cette page >>> Tissus et tissage >>> Toile ou drap >>> Sergé >>> Satin |
>>> Historique >>> Échiquier des tissus >>> Famille des satins >>> Bilan |
Débutants Glossaire |
|
Il existe différents types de tissus. Ils sont
caractérisés par leur motifs de tissage, appelé armures,
comme l'armure satin ou l'armure velours. Les tissus à texture rectiligne sont composés de
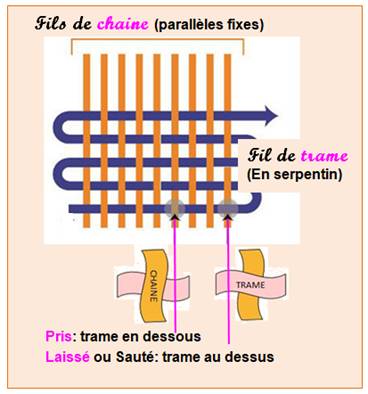
deux types de fils entrecroisés perpendiculairement: les fils de trame et les fils de chaine. Il existe trois armures simples: la toile,
le sergé et le satin.
Le velours est une armure complexe comprenant des fils supplémentaires qui
seront rasés. Note: satin et
velours ne sont pas des tissus mais des armures. La duite
désigne le point de passage de la trame à travers la chaine. Au dessus de la
trame c'est un pris et en dessous c'est un
laissé ou un sauté. Le motif de base, l'armure, se reproduit par
translations parallèles aux axes figurant ces deux fils. Il correspond généralement à une grille
carrée (un échiquier). Sa dimension p est le module
de l'armure (ou rapport d'armure). Sur une armure sont figurés les points de liage correspondant aux points du tissu où
s’opère la levée successive des fils de chaine, à chaque insertion de duite. L’échiquier carré associé à une armure comporte
un certain nombre de cases ombrées correspondant aux points de liage, les
fils de chaine étant représentés par les colonnes, ceux de trame par les
lignes de l’échiquier. |
Vocabulaire du tissage
Exemple de rendu (cas de la toile)
|
|
Vocabulaire de base du
tissage
|
Tissu Textile Toile Sergé Satin Velours Damas Fil |
Fabric Testile Tabby Twill Satin Velvet Damask Yarn, thread |
Tissage Armure Chaine Trame Pris Laissé ou sauté Duite Mèche Entrelacs |
Weaving Weave Warp Weft Taken Skipped Pick or shot Wick Interlocking |
Patron Métier Navette Cannette Écheveau |
Pattern Loom Shuttle Bobbin Skein |
Source: tout le vocabulaire du textile en diverses langues
|
Présentation La toile est la plus simple des armures dite
aussi armure unie, armure tabby, armure de
lin ou armure de taffetas L'armure toile est obtenue en soulevant
alternativement les fils pairs et les fils impairs de la chaîne, pour laisser
passage au fil de trame (duite). Tissage Dans un tissu à armure toile, les fils de chaîne
et de trame se croisent à angle droit, alignés de manière à former un simple
motif croisé. Chaque fil de trame croise les fils de chaîne en
passant au-dessus de l'un d'eux, puis sous le suivant, et ainsi de suite. Le
fil de trame suivant passe sous les fils de chaîne que son voisin a
traversés, et vice versa. Propriétés d'une toile Elle est solide et résistante, et elle est
utilisée pour les tissus de mode et d'ameublement.
Quelques toiles principales: la flanelle (laine),
la batiste (lin ou chanvre), le taffetas (en soie), le chambray (étym. de la
ville de Cambrai, proche du jean), la popeline (trame en laine et chaine en
soie). |
Principe du tissage et
représentation
Allure des entrecroisements
Exemple de rendu
|
|
Voir Brève
47-939
|
Présentation et tissage Le sergé est un type d'armure textile présentant
un motif de nervures diagonales parallèles. Il est fabriqué en faisant passer le fil de trame
sur un ou plusieurs fils de chaîne, puis sous deux ou plusieurs fils de
chaîne, et ainsi de suite, avec un "pas" ou un décalage entre les
rangs pour créer le motif diagonal caractéristique. Un sergé a un module de 3, et un décochement de
1. Propriétés du sergé :
Parmi les sergés on compte le Denim, tissu de
coton servant à fabriquer les jeans (étymologie: sergé de Nîmes, fabrication
dès 1557). |
Principe du tissage et représentation
Allure des entrecroisements et
exemple de rendu
|
|
|
Présentation et tissage Les tissus à armure satin sont plus souples et
présentent de meilleures caractéristiques de drapage que les armures unies
(toiles). Dans une armure satin, le fil de trame passe sur plusieurs
fils de chaîne avant de s'entrelacer sous un fil de chaîne. L'armure est caractérisée par des décochements
(sauts), à la fois en trame et en chaine, égaux à des nombres premiers avec
le module (excluant +1 et -1). Pour une armure de module 5, on aura donc deux
décochement possibles: 2 et 3. Propriétés du satin :
|
Principe du tissage et
représentation
Allure
des entrecroisements et exemple de rendu
|
|
|
En 1801, Joseph Jacquard met au point le premier métier à tisser, un système
mécanique programmable avec cartes perforées. En 1871, Édouard Gand (1815-1891), professeur de
dessin dans l’industrie du tissage souhaite pouvoir indiquer comment réaliser
sur les tissus des mosaïques, des combinaisons géométriques, des agencements
typiques de diverses cultures: chinoise, moresque, grecque, égyptienne. Il représente les différents
modes de tissage sur des motifs quadrillés. Il réalisera divers métiers, en particulier le
compositeur automatique (breveté) capable de générer par lui-même des motifs. Parmi les conclusions du travail de Gand: le
motif de l'armure est toujours un carré. "Le rapport longitudinal contient autant de duites que le rapport
transversal exige de chaine, c'est-à-dire que, dans tout papier quadrillé
destiné à une armure fondamentale donnée, il y aura toujours autant de cases
sur la hauteur de la mise en carte que de cases sur la largeur de cette mise
en carte" En 1867, Édouard Lucas (1842-1891), suite au travaux de Gand, publie: Application de l'Arithmétique à la
construction de l'armure des satins réguliers. Il y présente un classement
de tous les systèmes possibles
d'entrecroisement des fils de chaine et de trame. Il met en avant
l'utilisation des nombres premiers dans la construction des armures des
satins réguliers. En 1883,
il complète ces études et introduit les permutations figurées sur échiquier. Elles consistent en une disposition de n cases noires dans un carré
n × n de sorte à constituer une transversale
de carré latin (chaque ligne et chaque colonne ne contient qu’une case noire,
comme n tours placées sur un
échiquier de sorte que deux quelconques d’entre elles ne soient jamais en
prise. La géométrie du tissage sera reprise sous la
forme plus générale de l’étude des réseaux réguliers de points, et elle se
développe en prenant le nom de géométrie des
quinconces. L’intérêt mathématique des représentations géométriques obtenues
prime alors sur leur utilisation pratique. À titre d'exemple: Théorème des quinconces L'intérêt pour les mathématiciens devient tel que de nombreux
mathématiciens s'y intéressent, dont le groupe Bourbaki qui a développé un
chapitre particulier sur la géométrie des tissus. |
Les
explications qui suivent sont basées sur les livres
d'Édouard Lucas et de sur la thèse d'Anne-Marie Décaillot
|
SATIN Construire l’armure du satin régulier consiste à
considérer les cases d'un échiquier de
côté p. Alors, p pions sont disposés de
façon telle que deux d’entre eux ne se trouvent pas dans la même rangée
horizontale ou verticale (règle du carré
latin). Notez que les
pions (carrés grisés) sont décochés de (a) cellules en passant à la colonne
suivante et, en cas de dépassement de la grille, le pion est placé comme si
l'échiquier était enroulé
sur un cylindre. Pour réaliser un tissu, le motif est répété par
translation de sorte que les pions sont toujours placés de la même façon sur l'ensemble du tissu. Paramétrage Deux paramètres caractérisent l'armure satin:
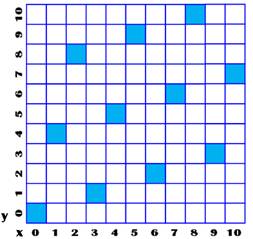
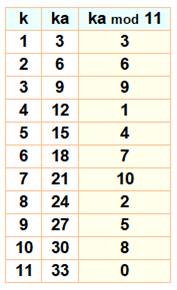
Moyen de calcul Les valeurs de y sont égales à (x · a mod p). Ce qui correspond aux valeurs successives de y:
(0, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7), ce qui est une des permutations des nombres de 0
à 10. Une autre permutation donnera un autre motif |
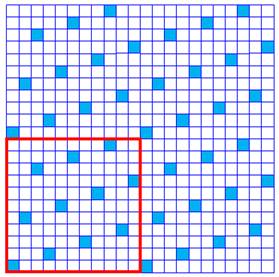
Satin (p = 11, a = 4)
Assemblage 2 x 2
|
||
|
Décochement et flotté Le décochement
(a < p), saut pour passer à la colonne suivante, est un nombre premier
avec p. Les indices de lignes (y) sont calculés en mod p
et les résidus ainsi obtenus constituent une permutation de nombres de 0 à p
– 1. Avec p = 11 et a = 4, on obtient la figure
indiquée ci-dessus. Les points bleus sont les points de liage. La distance en y entre deux points de
liage s'appelle le flotté. Un satin avec un grand flotté sera fragile et
brillant. |
Deux progressions Colonnes: Lignes: Il n'est pas interdit de donner une progression
arithmétique aussi aux colonnes (valeurs de x). Le premier pion est alors
placé au point (b, a). |
||
|
Calcul des restes (mod) Dans la progression arithmétique de raison a, les
termes divisés par p produisent des restes tous différents. En effet, prenons deux termes: m·a et n·a qui
auraient le même reste en les divisant par p. Alors (m – n) a
serait divisible par p. Comme p et a sont
premiers entre eux, cela signifierait que p
divise (m – n). Ce qui est impossible car (m – n) est inférieur à p. On rappelle que m et n ne dépassent pas p – 1. On note a' le
nombre k tel que aa'
= 1 mod p Sur l'exemple a' = 4.
C'est l'inverse de a = 3. |
Exemple avec p = 11 et a = 3
On retrouve tous les nombres de 0 à 10 en colonne de droite. |
||
|
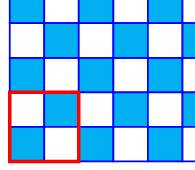
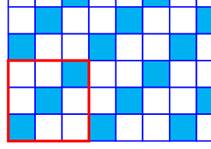
TOILE C'est un satin particulier de module p = 2 et de
décochement a = 1. Son motif est en damier. |
Armature (rouge) et morceau de
tissu obtenu
|
||
|
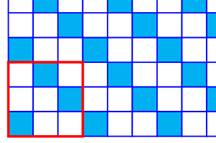
SERGÉ C'est un satin particulier de module p > 2 et
de décochement a tel que a = ± 1
mod p Illustration avec sergé (3, 1) en haut et (3, 2) en bas Les dessins (appelé serges)
qui leur correspondent par translation sont symétriques. |
Deux types de sergé
|
||
|
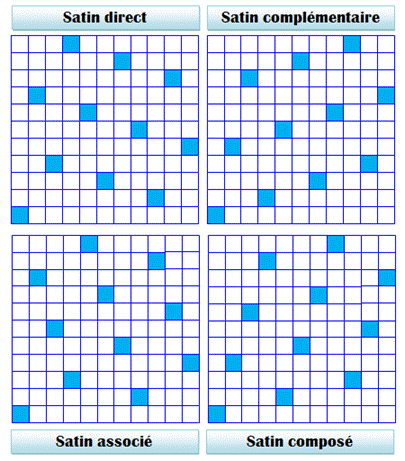
Famille Soit un satin (p, a), Son complémentaire est (p, p – a) Son associé est (p, a') Son associé complémentaire est (p, p – a') Exemple
Composé = associé et
complémentaire Observation Ces quatre armures sont identiques par
retournements selon cette illustration:
|
|
||||||||||||||||||||||||||
|
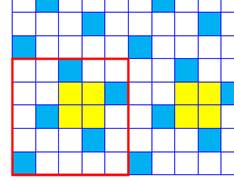
Satin carré Un satin est appelé carré lorsque l’inverse de a
est confondu avec son opposé, ce qui conduit à l’équation: a² + 1 = 0. Si p est premier, il doit être de la forme p = 4n + 1 (p est donc somme
de deux carrés). Mais, p peut être composé comme (25, 7 ou 26, 5). Le satin de module p = 5 et de décochement a = 2
est carré (Illustration) Celui de module p = 13 et de décochement a = 5. Ces types de satins passent pour être plus
élégants. |
Satin carré (5, 2) – Carré en jaune
|
||||||||||||||||||||||||||
|
Satin symétrique Avec a² – 1 = 0, le satin sera symétrique. Hors
toile et sergé, le module devra être composé (8, 3 par exemple). Les points de liages (case bleues) sont
symétriques par rapport à la diagonale principale et invariants par échange
trame-chaine. Le sergé est symétrique et la toile est la seule
à être à la fois carrée et symétrique. |
Satin symétrique (8, 3)
|
||||||||||||||||||||||||||
|
Une
approche, un petit voyage à travers ce monde des tissus. Il existe évidemment
de nombreuses variantes de tissage: avec deux fils, avec des fils de
différentes épaisseur, etc. Loin
d'être exhaustif ! Vous reporter aux sites spécialisés. Voir les documents en
référence. Notamment la thèse
d'Anne-Marie Décaillot qui
explique en détail les implications de la géométrie des tissus sur la théorie
des nombres, allant jusqu'à prouver la loi de la réciprocité
quadratique de Gauss (prouvée par E. Lucas. en 1890). Du
côté mathématique, les échiquiers ou grilles sont représentés par des matrices,
lesquelles permettent de faire des calculs divers. L'illustration montre un
motif obtenu par multiplication
de matrices. |
Exemples de tissus (il
en existe bien d'autres …)




Toile Sergé Satin Oxford
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Tissus.htm
|