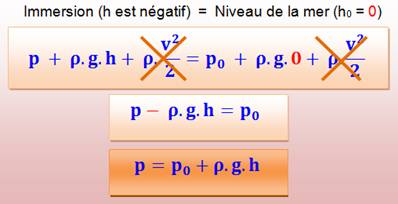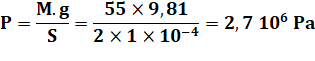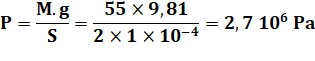|
|||||||||||||||||||||||||||||
![]()
Humour
|
Pascal, Newton et Einstein jouent
à cache-cache. C'est Einstein qui s'y colle. Pascal file et se cache derrière la maison. Newton
reste sur place et dessine un carré autour de lui. Einstein
a fini de compter et découvre Newton devant lui. – Dis donc, Newton, fastoche
pour te trouver ! – Mais, Einstein, tu te trompes de personne, c'est Pascal
que tu viens de trouver. Il montre le carré et poursuit: c'est un newton dans un mètre carré. |
Voir Pensées & humour
|
PRESSION Témoin du poids d'un fluide:
air ou eau ou d'un solide … L'unité de pression dans le système SI est le pascal (Pa) La forme du récipient n'a aucune influence sur la pression. Tous les points situés à la même profondeur sont à la
même pression. Expérience du crève-tonneau réalisée par Pascal: un tonneau et
un fin tube le surmontant. L'eau dans le tube (un litre, par exemple, sur une
hauteur suffisante) fait éclater le tonneau. |
|
|
||
|
Pascal (Pa) Pression exercée par une
force de 1 newton qui se trouve appliquée à une surface de 1 m² En gros: " un dixième de kg sur
1m² " 1Pa = 1
N / m² =
1/100 hPa (hectopascal) = 10
-5 bar =
1/100 mbar (millibar) 1000
hPa = 1 bar 1 hPa = 1 millibar |
Pression
p =
p = Pression hydrostatique
|
|
Voir Les notions de base
|
En gros et pour les retenir |
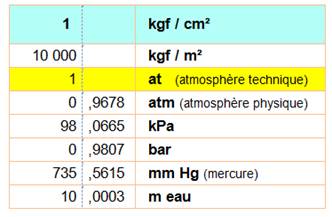
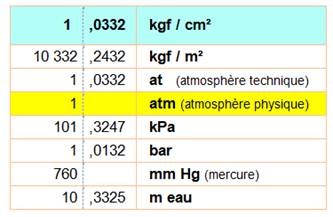
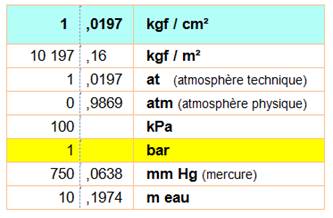
Correspondance avec d'autres unités de pression |
|||||||||||||||||||||||||||
|
Une pression de 1 kilogramme-poids sur un
cm² vaut: 1 kp / cm² 1 atmosphère 1 bar 100 000 pascals 100 000 N / m² |
Valeur en pascals
|
Voir Unités et
conversion / Voir site Convertworld.com
|
|
||
|
1 bar ou 1000 hPa tous les 10 mètres |
La pression augmente considérablement sous
l'eau. Imaginer la pression sur un sous-marin à 300 mètres d'immersion! 30
bars = 30 kilogramme-poids par cm². |
|
|
|
||
|
|
|||
|
Pour tout fluide en écoulement, la somme de ces trois termes est
constante; que l'on mesure ici ou là, cette expression donne le même
résultat. |
|
||
|
Sans écoulement, le troisième terme disparait, et au niveau de la mer
la hauteur est égale à zéro. |
|
||
|
h est
l'immersion (en mètres); p est la
pression à l'immersion h (en N.m-2); p0
est la pression au niveau de l'eau (pression atmosphérique);
g est l'accélération de la pesanteur: 9,81 m.s-2. 1 bar =
105 pascals. |
p = p0 + 1025 x 9,81 . h p = p0 + 10 055 h p p |
||
|
Nous retrouvons notre résultat: La pression augmente de 1
bar tous les 10 mètres d'immersion. |
|||
Voir Daniel Bernoulli
/ Vitesse du jet
|
|
||
|
Poids
d'une colonne d'air de 1 m² sur toute la
hauteur de l'atmosphère: 101 325 pascals =
1013,25 hPa =
1013,25 millibar » 1 bar =
1 atmosphère » 10 000 kg sur une surface horizontale de 1 m² |
Pression atmosphérique
standard (AOCI) au niveau de la mer à 15°C. Correspondant à 760 mm de mercure. 1 mm Hg |
|
|
Comme
un plongeur subit la pression de l'eau, nous subissons tous la |
|
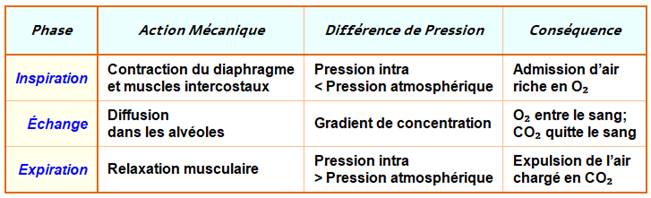
Attention
! Nous n'aspirons pas de
l'air en respirant; nous faisons de la place dans la cage thoracique pour
que l'air, sous l'effet de la pression atmosphérique, s'engouffre dans nos
poumons. Nos poumons sont comme une poche molle. Pas de muscles. L’inspiration est
associée à une augmentation du
volume de la cage thoracique, une diminution de la pression dans les poumons et une entrée de l’air de l’extérieur
vers les poumons. L’expiration est
associée à une diminution du
volume de la cage thoracique, une augmentation de la pression dans les poumons et une sortie de l’air des poumons
vers l’extérieur. Outre les différences de
pression, la respiration dépend également de la contraction et de la
relaxation des fibres musculaires du diaphragme et du thorax. Les poumons
eux-mêmes sont passifs lors de la respiration, ce qui signifie qu'ils ne
participent pas à la création du mouvement qui favorise l'inspiration et
l'expiration. Cela est dû à la nature adhésive du liquide pleural, qui permet
de tirer les poumons vers l'extérieur lorsque la paroi thoracique bouge
pendant l'inspiration. Le recul de la paroi thoracique lors de l'expiration
provoque une compression des poumons. La contraction et la relaxation du
diaphragme et des muscles intercostaux (situés entre les côtes) sont à
l'origine de la plupart des changements de pression qui entraînent
l'inspiration et l'expiration. Ces mouvements musculaires et les changements
de pression qui s'ensuivent amènent l'air à entrer ou à sortir des poumons. Suite en : Le
processus de la respiration - LibreTexts En résumé
|
Voir Corps
humain / Respiration – Volume / Brève 63-1241
|
Historique Galilée À l'époque de Galilée, les fontainiers avaient remarqué que l'eau ne
pouvait être élevée à plus de 10 mètres par une pompe aspirante. Sollicité Galilée
n'avait pas pu expliquer le phénomène. |
|
|
Torricelli C'est Evangelista Torricelli qui, en 1643, comprit le rôle clef de la
force due à la gravitation dans ce problème. Il réalisa une
expérience avec du mercure à la place de l'eau. |
|
|
L'idée de
Torricelli était que l'atmosphère exerce une même force sur tous les objets. |
|
|
Pascal Pascal prolonge le raisonnement: la force
exercée par l'atmosphère est due au poids de l'atmosphère elle-même. Il en déduit que la
pression atmosphérique doit diminuer avec l'altitude. Naturellement, elle
varie aussi selon les conditions météorologiques. |
au Puy de dôme, et à la
Tour Saint Jacques à Paris. |
|
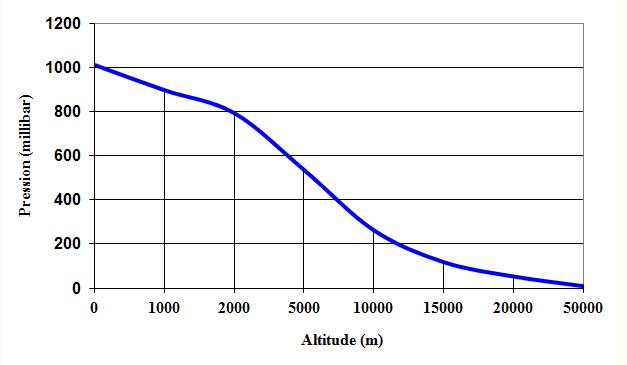
Variation de la pression (standard) en
fonction de l'altitude
Attention:
abscisses
non linéaires
1 mbar tous les 10
mètres jusqu'à 2 000. 1
hPa tous les 15 mètres jusqu'à 10 000.
7 ° C tous les 1 km.
|
|
Voir Pompes et pression atmosphérique
|
|
||
|
|
27
cm x 21 cm x 4,5 cm 2
kg |
|
|
|
F
= m . g = 2kg x 9,81kg.m/s² = 19,62 N |
|
|
|
S = 0,27m x 0, 21m =
0,0567 m² |
|
|
|
P = F/S = 19,62 / 0,0567 = 346,0 Pa |
|
|
|
S = 0,21m x 0, 045m =
9,45 10-3 m² |
|
|
|
P = F/S = 19,62 / 9,45 10-3 = 2
076 Pa |
|
|
|
70 kg Chaque pied: 192 cm² (pointure 43) |
|
|
|
|
|
|
|
55 kg 1 cm² |
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()