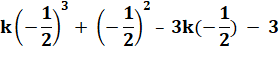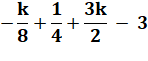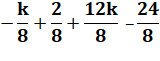|
||||||||||||||||||||||||||||
![]()
|
POLYNÔMES - Exercices Exemples de traitement
effectués sur les polynômes. Connaissance des racines d'où connaissance de la
factorisation. |
|
|
|||
|
Problème |
|
|
|
|
Si |
kx3 + x2
– 3kx – 3 |
est divisible par 2x + 1 |
|
|
Trouvez |
k |
= ? |
|
|
Rappel |
Si ax + b est facteur de P(x) |
alors P(-b/a) = 0
|
|
|
Solution |
|
|
|
|
Application du
théorème |
P(-1/2) |
= 0 |
|
|
Calculs |
|
= 0 |
|
|
|
|
= 0 |
|
|
|
|
= 0 |
|
|
|
11 k |
= 22 |
|
|
Valeur de k |
k |
= 2 |
|
|
Problème |
Si x5 – ax + b |
est divisible par x2 – 4 |
|
Trouvez |
a et b |
= ? |
|
Racines |
x2 – 4 |
= (x – 2) (x + 2) |
|
f(–2) f(2) |
= (–2)5 – a(–2) + b = –32 + 2a + b = 0 = (2)5 – a(2) + b = 32 – 2a + b = 0 |
|
|
Résolution du système |
Soustraction |
–32 + 2a + b = 0 32 – 2a + b = 0 –64 + 4a + 0 = 0 |
|
Substitution |
–32 + 2.16 + b = 0 |
|
|
Conclusion et vérification |
x5 – 16x = x(x4 – 16) |
est divisible par x2 – 4 = (x² – 4) (x² + 4) x |
|
|
|||
|
Problème |
f(x) |
est divisible par x2 – 4 a pour racine –3 et 6 |
|
|
Trouvez |
f(x) |
= ax4 + … |
|
|
Racines |
–3 6 |
f(x) = (x + 3) g(x) f(x) = (x + 3) (x – 6)
g'(x) |
|
|
x2 – 4 |
apporte deux racines (–2 et +2) |
||
|
Polynôme |
du quatrième degré |
nous disposons des quatre racines |
|
|
Calcul |
f(x) |
= (x + 3) (x – 6) (x2 – 4) = (x2 – 3x – 18) (x2 – 4) = x4 – 3x3 – 18x2 – 4x2 +
12x + 72 = x4 – 3x3 – 22x2 + 12x + 72 |
|
|
|
|||
|
Problème |
|
|
|
|
Prouvez que g(x) divise f(x) |
g(x) = x2 – 1 |
f(x) = 10x4 + 9x3 – 2x2 – 9x – 8 |
|
|
Racines |
de x2 – 1 |
= {–1 et +1} |
|
|
Calcul de f(racines) |
f(–1) f(1) |
= 10 – 9 – 2
+ 9 – 8 = 0 = 10 + 9 – 2 – 9 – 8 = 0 |
|
|
Théorème du reste |
–1 et +1 sont bien racines de
f(x); (x – 1) (x + 1) = x2 – 1 divise f(x). |
||
|
Problème |
Note: on utilise y et non x pour ne pas confondre avec
le signe multiplier. |
|
|
Prouvez que g(y) divise f(y) |
g(y) = y2 + 5y +
6 |
f(y) = 10y4 + 59y3 + 113y2 + 94y +
48 |
|
Racines |
g(y) = y2 + 5y +
6 |
= (y – a) (y – b) = y2 + y(–a – b) + ab |
|
ab = 6 et a + b = –5 a = –2 et b = –3 (ou inversement) |
||
|
Calcul de f(racines) |
f(–2) f(–3) |
= 10x16 – 59x8 + 113x4 – 94x2 + 48 = 160 – 472 + 452 – 188 + 48 = 10*81 – 59x27 + 113x9 – 94x3 + 48 = 810 –
1593 + 1017 – 282 + 48 = |
|
Théorème du reste |
–2 et –3 sont bien racines de
f(y); (y + 2) (y + 3) = y2
+ 5y + 6 divise f(y). |
|
|
|
|||
|
Problème |
Ajoutez un polynôme h(y) de degré 3 pour que g(y)
divise f(y) + h(y) |
||
|
g(y) = y2 + 5y +
6 |
f(y) = y3 + 15y2 + 5y + 18 |
||
|
Racines |
g(y) = y2 + 5y +
6 |
= (y – 2) (y – 3) cf. ci-dessus |
|
|
Somme des
polynômes |
f(y) + h(y) |
= y3 + 15y2
+ 5y + 18 + ay3 + by2
+ cy + d = (a+1)y3 +
(b+15)y2 + (c+5)y + d+18 |
|
|
Calcul de
f(racines) |
f(–2 ) + h(–2) |
= –(a+1)8 + (b+15)4 –
(c+5)2 + d + 18 = –8a + 4b – 2c + d – 8 +
60 – 10 + 18 = –8a + 4b – 2c + d + 60 |
|
|
f(–3 ) + h(–3) |
= –(a+1)27 + (b+15)9 –
(c+5)3 + d + 18 = –27a + 9b – 3c + d – 27
+ 135 – 15 + 18 = –27a + 9b – 3c + d +
111 |
||
|
Consigne |
Les restes |
doivent
être nuls pour assurer la divisibilité. |
|
|
Résolution (2 équations pour ' inconnues) |
Soustraction |
–8a + 4b – 2c + d + 60 =
0 –27a + 9b – 3c + d + 111
= 0 19a – 5b + c – 51 = 0 c = 51 – 19a + 5b |
|
|
Substitution |
–8a + 4b – 2(51 – 19a + 5b) + d + 60 = 0 = 30a – 6b – 102 + d + 60
d = 42 – 30a + 6b |
||
|
Avec par exemple a = b = 0 |
Valeurs de c et d |
c = 51 d = 42 |
|
|
Un des polynômes à ajouter |
h(y) |
= ay3 + by2
+ cy + d = 51y + 42 |
|
|
Polynôme somme |
f(y) + h(y) |
= y3 + 15y2
+ 5y + 18 + 51y + 42 = y3 + 15y2
+ 56y + 60 |
|
|
Vérification |
f(-2) + h(-2) f(-3) + h(-3) |
= –8 + 60 – 112 + 60 = 0 = –27 + 135 – 168 + 60 = 0 |
|
|
|
|||
|
Problème |
|
|
|
|
Prouvez que: |
f(x) = (x + 1)2n
+ (x + 2)n – 1 |
est divisible
par x² + 3x + 2 = g(x) |
|
|
Racines |
de x² + 3x + 2 |
= {-1 et -2} |
|
|
Solution |
f(-1) |
= (-1+1)2n + (-1+2)n – 1 =
0 |
|
|
|
f(-2) |
= (-2+1)2n + (-2+2)n – 1 =
0 |
|
|
Ce qui veut dire que |
les racines de g(x) |
sont aussi celles de f(x) |
|
|
Propriété |
(x+1) |
|
|
|
Or |
x+1 et x+2 |
sont deux nombres consécutifs et sont premiers
entre eux |
|
|
Leur PPCM et le produit |
PPCM(x+1, x+2) |
= (x+1) (x+2) = x² + 3x + 2 = g(x) |
|
|
|
g(x) |
divise f(x)
|
|
|
|
|||
|
Problème |
|
|
|
|
Polynômes: |
P et Q: |
à coefficients réels |
|
|
Si |
Si (x – a)2 divise et (x – a)3 ne divise pas |
P(x)3 – Q(x)3 |
|
|
Montrer que: |
Alors (x – a)2 divise |
P(x) – Q(x) |
|
|
Autrement-dit |
Si P3 – Q3
|
= (x – a)² R = (x – a)² T |
|
|
|
a est racine |
double mais pas triple |
|
|
Démonstration |
|
|
|
|
Factorisation: |
P3 – Q3 |
= (P – Q) (P² + PQ + Q²) |
|
|
Selon l'énoncé: |
a est racine double de |
(P – Q) (P² + PQ + Q²) |
|
|
Faisons cette hypothèse et montrons qu'elle est
fausse. |
a est racine de |
P² + PQ + Q² |
|
|
Alors avec a: |
P²(a) + Q²(a) |
= –P(a) Q(a) |
|
|
Cette égalité montre que: |
0 |
|
|
|
Carré de P+ Q avec a: |
( P(a) + Q(a) )² |
= P²(a) + Q²(a) + 2 P(a)Q(a) = –P(a) Q(a)
+ 2 P(a)Q(a) =
P(a)Q(a) |
|
|
Cette égalité montre que: |
0 |
|
|
|
Double inégalité qui impose: |
0 |
= P(a) Q(a) |
|
|
Alors: |
a est racine de |
P ou Q |
|
|
Si a racine de P |
P3(a) |
= 0 |
|
|
Or a est racine de P3 – Q3. |
P3(a) – Q3(a) |
= 0 |
|
|
Conséquence: a est aussi racine de Q. |
Q(a) |
= 0 |
|
|
a est racine de P – Q |
P(a) – Q(a) |
= 0 racine simple au moins |
|
|
Or a est racine de l'autre facteur (notre
hypothèse). |
P²(a) + P(a)Q(a) + Q²(a) |
= 0 racine double au moins |
|
|
Sur le produit des deux facteurs: |
P3(a) – Q3(a) |
= 0 racine au moins triple |
|
|
Contraire à l'énoncé. |
a |
n'est pas
racine triple |
|
|
Hypothèse fausse: |
a n'est pas racine de |
P² + PQ + Q² |
|
|
a est racine double (selon l'énoncé), |
mais uniquement sur |
P – Q |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()