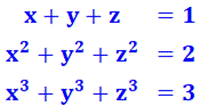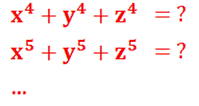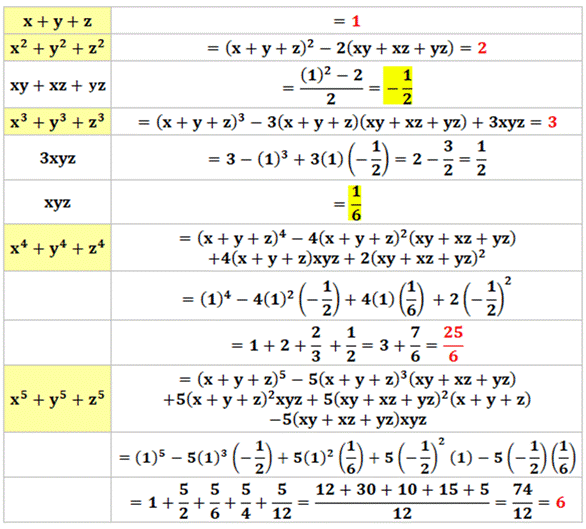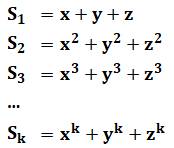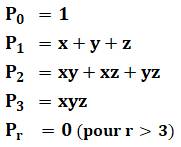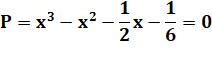|
Édition du: 12/09/2023 |
|
INDEX |
Polynômes |
||
|
(Girard-Newton) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Somme de puissances Identité de Girard-Newton Approche à l'aide d'une énigme Défi
Trois
méthodes pour relever ce défi concernant le calcul de la somme
des puissances:
|
||
|
|
Sommaire de cette page >>> Le défi et les polynômes symétriques >>> Identité de Girard-Newton >>> Calcul des racines >>> Calcul des racines avec Maple |
Technique de base de l'algèbre |
|
Défi Connaissant la somme de trois variables, chacune à
la même puissance de degré 1, 2 et 3, le défi consiste à calculer la somme
pour les puissances supérieures. Ces sommes sont des polynômes
symétriques (x, y et z sont interchangeables). Le théorème
fondamental des fonctions symétriques indique que toute fonction
symétrique est décomposable en fonctions symétriques élémentaires. Nous allons résoudre cette énigme en utilisant la
table de telles décompositions. |
|
|
|
Polynômes symétriques élémentaires
(PSE) Avec trois variables, ils sont seulement trois. Le premier (la somme) est connu. Il s'agit de
calculer les deux autres avec les sommes de carrés et de cubes. Ce sera suffisant pour calculer toutes les sommes
de puissances supérieures. |
Les trois PSE à trois variables x + y + z xy + yz + zx xyz |
|
|
Principe du calcul La somme des puisances (symétrique) est toujours une
combinaison des trois polynomes symétriques élementaires. Ceux-ci sont connus
dés que l'on connait la somme des entiersn des carrés et des cubes.
|
||
Voir Factorisation des
équations du troisième degré
|
Calculs
Évidemment le calcul pour les puissances
supérieures nécessite de connaitre la table de décomposition pour les
puissances concernées. |
|
Notations On commence par nommer les sommes (S) de
puissances. De même pour les polynômes (P) symétriques
élémentaires à 3 variables. |
|
||
|
L'identité de Girard-Newton s'écrit |
|
||
|
Ce que nous savons avec notre énigme |
S1
= P1 = 1 S2
= 2 S3
= 3 |
||
|
Calcul avec k = 2 |
|
||
|
Calcul avec k = 3 |
|
||
|
Calcul avec k = 4 Sachant que P4 = 0 |
|
||
|
Calcul avec k = 5 Sachant que P5 = 0 |
|
||
|
Calcul avec k = 6 Sachant que P6 = 0 |
|
||
|
Calcul avec k = … |
Cette méthode est simple, y compris pour les
calculs des sommes pour de grandes puissances. En effet, les termes avant les
quatre derniers sont toujours nuls. |
||
|
Ce sont les trois racines d'un polynôme du
troisième degré. |
Polynôme avec racines a, b, et c P = (x – a)(x – b)(x – c) Polynôme développé P = x3 – (a+b+c)x2 +
(ab+ac+bc)x – abc |
||
|
En l'occurrence on connait les expressions avec les
coefficients. Ce sont les trois polynômes symétriques élémentaires. Leur valeur est connue. |
Équation
|
||
|
La résolution est fastidieuse. Un logiciel de calcul donne la solution. |
|
||
Allure des racines. Bon courage
si vous vous décidez à résoudre cette équation à la main

|
Suite
|
But Calculer les racines de ce système d'équations
(bleu) et la somme des puissances (rouge) Commentaires Solve résout le
système, mais la mise en forme des trois racines nécessite quelques
traitements. Evalf pour obtenir
les valeurs numériques. On a demandé 20 chiffres de précision (Digits). Op(E[1])[2] pour extraire la
1ère racine [1] et sa valeur [2]. Calcul de la
somme des puissances k pour k de 1 à 10. Identify évite les
nombres tels que 1,999… en donnant 2. Solution Wolfram Vous pouvez
aussi obtenir ces racines en ligne avec le logiciel WolframAlpha |
|
Voir Programmation – Index
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |