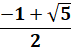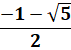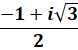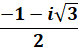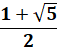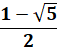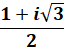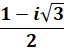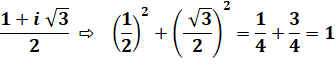NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 11/04/2021

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique           Brèves de Maths   

Algèbre

 

Débutants

Technique de base

de l'algèbre

POLYNÔMES

 

Glossaire

Polynômes

 

 

INDEX

Polynômes

 

Arithmétique et algèbre

Introduction

Propriétés

Division

Divisibilité

Unitaire

Exercices

Ex. de divisions

 

Sommaire de cette page

>>> Définition et liste

>>> Deuxième degré

>>> Troisième degré

>>> Quatrième degré

>>> Cinquième degré

 

 

 

Propriétés des polynômes unitaires

et racines dans le disque unité

Kronecker Polynomials (KP)

 

Définition et liste

 

On considère les polynômes unitaires à coefficients entiers dont les racines sont toutes dans le disque unité.

 

Polynôme unitaire: il a 1 comme coefficient du degré le plus élevé.

Disque unité: tout point est  à une distance de l'origine inférieure ou égale à 1.

 

Un théorème de Kronecker affirme que: la quantité Q de ces polynômes est finie. Ce sont les polynômes de Kronecker (KP).

 

They are finitely many monic polynomials of degree n with integer coefficients and all zeros in the unit disc.

 

 

Liste de la quantité des KP

pour des degrés croissants à partir de 0

 

1, 3, 9, 19, 43, 81, 159, 277, 501, 831, 1415, 2253, 3673, 5675, 8933, 13447, 20581, 30335, 45345, 65611, 96143, 136941, 197221, 276983, 392949, 545119, 763081, 1046835, 1448085, 1966831, 2691697, 3622683, 4909989, 6553615, 8804153, …

 

Exemple

 

Q(1) = 3 avec [z, z + 1 et z – 1]

Les racines 0, -1 et +1 sont à l'évidence dans le disque unitaire.

 

 

Dénombrement

Il peut être effectué de manière directe en les listant comme ci-dessous pour le degré 2.

 

 

Une méthode plus efficace consiste à recourir aux polynômes cyclotomiques (racines de l'unité).

En effet, Damianou a prouvé que les PK s'exprime aussi avec:
PK(x) = xk Q(x)
avec Q un produit fini de polynômes cyclotomiques.

 

 

 

Deuxième degré


 

Avec la combinaison des valeurs de a et b, il y a quinze polynômes unitaires de degré 2.

En limitant les racines à 1 ou moins, six d'entre eux sont éliminés (en ocre dans le tableau).

Il y a neuf KP (en jaune dans le tableau.

 

 

Tableau des 9 polynômes unitaires de degré 2

2-Unitaire

Factorisation

Racines

Racines (numériques)

z² + 2z – 1

 z² + 2z – 1

0,4142…

– 2,4142…

z² + 2z

 z(z + 2)

– 2

0

– 2

0

z² + 2z + 1

 (z + 1)²

– 1

– 1

– 1

– 1

z² + z – 1

 z² + z – 1

0,6180…

– 1,6180…

z² + z

 z(z + 1)

-1

0

– 1

0

z² + z + 1

 z² + z + 1

– 0,5+.8660… i

module  = 1

– 0,5 – 0,8660… i

module  = 1

z² – 1

 (z – 1)(z + 1)

1

-1

1

– 1

z²

 z²

0

0

0

0

z² + 1

 z² + 1

i

–i

i

– i

z² – z – 1

 z² – z – 1

1,6180…

– 0,6180…

z² – z

 z(z – 1)

0

1

0

1

z² – z + 1

 z² – z + 1

0,5 + 0,8660… i

module  = 1

0,5 – 0,8660… i

module  = 1

z² – 2z – 1

 z² – 2z – 1

2,4142…

– 0,4142…

z² – 2z

 z(z – 2)

0

2

0

2

z² – 2z + 1

 (z – 1)²

1

1

1

1

 

Exemple de calcul du module dans le cas d'une racine complexe

 

Avec 1, -1,  i ou – i  le module vaut également 1.

 

D'une manière générale pour tous les KP, le module de toutes  les racines non nulles est 1.

Les racines sont sur la circonférence du disque unité et jamais à l'intérieur, sauf celles au centre.

 

 

Troisième degré


 

Avec la combinaison des valeurs de a, b et c, il y a 147 polynômes unitaires de degré 3.

En limitant les racines à 1 ou moins, il reste 19  KP.

  

Liste des coefficients des KP

 

[a, b, c]

[-3, 3, -1], [-2, 1, 0], [-2, 2, -1], [-1, -1, 1], [-1, 0, 0], [-1, 1, -1], [-1, 1, 0], [0, -1, 0], [0, 0, -1], [0, 0, 0], [0, 0, 1], [0, 1, 0], [1, -1, -1], [1, 0, 0], [1, 1, 0], [1, 1, 1], [2, 1, 0], [2, 2, 1], [3, 3, 1]

 

 

Tableau des 19 polynômes unitaires de degré 3 avec racines dans le disque unitaire

3-Unitaire

Factorisation

Racines

z3 + 3z2 + 3z + 1

 (z + 1)3

 -1

 – 1

 – 1

z3 + 2z2 + z

 z(z + 1)2

 0

 – 1

 – 1

z3 + 2z2 + 2z + 1

 (z + 1)(z2 + z + 1)

 -1

 – 0,5 – 0,8660… i

 – 0,5 + 0,8660… i

z3 + z2 – z – 1

 (z – 1)(z + 1)2

 1

 – 1

 – 1

z3 + z2

 z2(z + 1)

 -1

 0

 0

z3 + z2 + z

 z(z2 + z + 1)

 0

 – 0,5 + 0,8660… i

 – 0,5 –  0,8660… i

z3 + z2 + z + 1

 (z + 1)(z2 + 1)

 -1

 i

 – i

z3 – z

 z(z – 1)(z + 1)

 0

 1

 – 1

z3 – 1

 (z – 1)(z2 + z + 1)

 1

 – 0,5 – 0,8660… i

 – 0,5 + 0,8660… i

z3

 z3

 0

 0

 0

z3 + 1

 (z + 1)(z2 – z + 1)

 -1

 0,5 – 0,8660… i

 0,5 + 0,8660… i

z3 + z

 z(z2 + 1)

 0

 i

 – i

z3 – z2 – z + 1

 (z + 1)(z – 1)2

 -1

 1

 1

z3 – z2

 z2(z – 1)

 1

 0

 0

z3 – z2 + z – 1

 (z – 1)(z2 + 1)

 1

i

 – i

z3 – z2 + z

 z(z2 – z + 1)

 0

 0,5 + 0,8660… i

 0,5 – 0,8660… i

z3 – 2z2 + z

 z(z – 1)2

 0

 1

 1

z3 – 2z2 + 2z – 1

 (z – 1)(z2 – z + 1)

 1

 0,5 – 0,8660… i

 0,5 + 0,8660… i

z3 – 3z2 + 3z – 1

 (z – 1)3

 1

 1

 1

 

 

Quatrième degré


 

Avec la combinaison des valeurs de a, b, c et d, il y a 1 323 polynômes unitaires de degré 4.

En limitant les racines à 1 ou moins, il reste 43  KP.

 

attention.png Mon calcul avec logiciel ne m'en donne que 41. Explication ? Des solutions doubles ?

  

Liste des coefficients des 41 KP détectés avec mon logiciel.

Alors qu'il en existerait 43.

 

[a, b, c, d]

[-3, 3, -1, 0], [-3, 4, -3, 1], [-2, 0, 2, -1], [-2, 1, 0, 0], [-2, 2, -2, 1], [-2, 2, -1, 0], [-2, 3, -2, 1], [-1, -1, 1, 0], [-1, 0, -1, 1], [-1, 0, 0, 0], [-1, 0, 1, -1], [-1, 1, -1, 0], [-1, 1, -1, 1], [-1, 1, 0, 0], [-1, 2, -1, 1], [0, -2, 0, 1], [0, -1, 0, 0], [0, -1, 0, 1], [0, 0, -1, 0], [0, 0, 0, -1], [0, 0, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0], [0, 1, 0, 0], [0, 1, 0, 1], [0, 2, 0, 1], [1, -1, -1, 0], [1, 0, -1, -1], [1, 0, 0, 0], [1, 0, 1, 1], [1, 1, 0, 0], [1, 1, 1, 0], [1, 1, 1, 1], [1, 2, 1, 1], [2, 0, -2, -1], [2, 1, 0, 0], [2, 2, 1, 0], [2, 2, 2, 1], [2, 3, 2, 1], [3, 3, 1, 0], [3, 4, 3, 1]

 

 

Cinquième degré

Liste des coefficients des 75 KP de degré 5 détectés avec mon logiciel.

Alors qu'il en existerait 81.

 

[a, b, c, d, e]

[-3, 2, 2, -3, 1], [-3, 3, -1, 0, 0], [-3, 4, -4, 3, -1], [-3, 4, -3, 1, 0], [-3, 5, -5, 3, -1], [-2, 0, 2, -1, 0], [-2, 1, -1, 2, -1], [-2, 1, 0, 0, 0], [-2, 1, 1, -2, 1], [-2, 2, -2, 1, 0], [-2, 2, -2, 2, -1], [-2, 2, -1, 0, 0], [-2, 3, -3, 2, -1], [-2, 3, -2, 1, 0], [-1, -2, 2, 1, -1], [-1, -1, 1, 0, 0], [-1, -1, 1, 1, -1], [-1, 0, -1, 1, 0], [-1, 0, 0, -1, 1], [-1, 0, 0, 0, 0], [-1, 0, 0, 1, -1], [-1, 0, 1, -1, 0], [-1, 1, -1, 0, 0], [-1, 1, -1, 1, -1], [-1, 1, -1, 1, 0], [-1, 1, 0, 0, 0], [-1, 1, 1, -1, 1], [-1, 2, -2, 1, -1], [-1, 2, -1, 1, 0], [0, -2, 0, 1, 0], [0, -1, -1, 0, 1], [0, -1, 0, 0, 0], [0, -1, 0, 1, 0], [0, -1, 1, 0, -1], [0, 0, -1, 0, 0], [0, 0, 0, -1, 0], [0, 0, 0, 0, -1], [0, 0, 0, 0, 0], [0, 0, 0, 0, 1], [0, 0, 0, 1, 0], [0, 0, 1, 0, 0], [0, 1, -1, 0, -1], [0, 1, 0, 0, 0], [0, 1, 0, 1, 0], [0, 1, 1, 0, 1], [0, 2, 0, 1, 0], [1, -2, -2, 1, 1], [1, -1, -1, 0, 0], [1, -1, -1, 1, 1], [1, 0, -1, -1, 0], [1, 0, 0, -1, -1], [1, 0, 0, 0, 0], [1, 0, 0, 1, 1], [1, 0, 1, 1, 0], [1, 1, -1, -1, -1], [1, 1, 0, 0, 0], [1, 1, 1, 0, 0], [1, 1, 1, 1, 0], [1, 1, 1, 1, 1], [1, 2, 1, 1, 0], [1, 2, 2, 1, 1], [2, 0, -2, -1, 0], [2, 1, -1, -2, -1], [2, 1, 0, 0, 0], [2, 1, 1, 2, 1], [2, 2, 1, 0, 0], [2, 2, 2, 1, 0], [2, 2, 2, 2, 1], [2, 3, 2, 1, 0], [2, 3, 3, 2, 1], [3, 2, -2, -3, -1], [3, 3, 1, 0, 0], [3, 4, 3, 1, 0], [3, 4, 4, 3, 1], [3, 5, 5, 3, 1]

 

 

 

Programme Maple pour les 3-KP

 

 

But

Trouver les valeurs des coefficients a, b et c des KP du troisième degré.

 

Commentaires

Réinitialisation, Initialisation de compteurs et d'une liste L.

Boucles d'exploration des tris coefficients.

Calcul du polynôme, sa factorisation et ses racines, y compris les racines en décimal (evalf).

Test si ces racines en valeurs absolues sont inférieures ou égale à 1. Dans le cas d'une racine complexe, la valeur absolue est bien la racine de la somme des carrés.

La liste est mise à jour dans le cas positif.

Enfin, on demande d'imprimer la quantité totale de polynômes (kt), la quantité des KP et la liste des coefficients.

 

Voir Programmation – Index

 

 

 

Suite

*         Exercices sur ce thème

Voir

*         Polynômes – Index

*         Factorisation du polynôme du second degré

Site

*            OEIS A051894 - Number of monic polynomials with integer coefficients of degree n with all roots in unit disc

*            Monic Polynomials in Z[x] with Roots in the Unit Disk – Pantelis A. Damianou

*            On Kronecker Polynomials – Ahmed Ayache, Othman Echi et Mongi Naimi – pdf 19 pages

Cette page

http://villemin.gerard.free.fr/aMaths/Polynome/Unitaire.htm