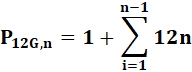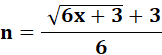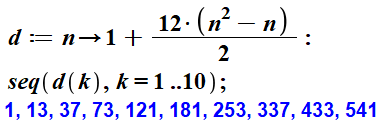|
Édition du: 22/06/2020 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
NOMBRES DODÉCAGONAUX CENTRÉS 12-gonal centrés Nombres
construits en déposant des points sur des décagones concentriques. |
||
|
|
Sommaire de cette page >>>
Nombres décagonaux >>>
Nombres décagonaux – Tables >>>
Propriétés avec les nombres triangulaires ff |
Débutants Nombres
figurés ou
géométriques Glossaire |
|
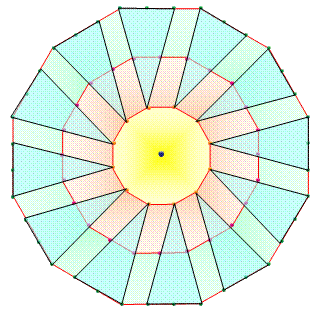
Construction des nombres
dodécagonaux
Le rang n correspond à la quantité de billes sur
un côté du polygone. La quantité de billes est cumulée pour passer
d'un nombre ennéagonal au suivant. |
|
|||||||||||||||||||||||||||||
|
Notation et formules |
|
|||||||||||||||||||||||||||||
|
Caractérisation Sorte de racine dodécagonale centrée. |
Si
n est un nombre entier alors x est le énième nombre dodécagonal. Sinon, il
n'est pas hexagonal. N
est une des racines de x = 6n² – 6n |
|||||||||||||||||||||||||||||
|
Programme |
|
|||||||||||||||||||||||||||||
|
Nombres
décagonaux centrés – Tables |
||
|
Les 100 premiers dodécagonaux
centrés |
1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793,
937, 1093, 1261, 1441, 1633, 1837, 2053, 2281, 2521, 2773, 3037, 3313, 3601,
3901, 4213, 4537, 4873, 5221, 5581, 5953, 6337, 6733, 7141, 7561, 7993, 8437,
8893, 9361, 9841, 10333, 10837, 11353, 11881, 12421, 12973, 13537, 14113,
14701, 15301, 15913, 16537, 17173, 17821, 18481, 19153, 19837, 20533, 21241,
21961, 22693, 23437, 24193, 24961, 25741, 26533, 27337, 28153, 28981, 29821,
30673, 31537, 32413, 33301, 34201, 35113, 36037, 36973, 37921, 38881, 39853,
40837, 41833, 42841, 43861, 44893, 45937, 46993, 48061, 49141, 50233, 51337,
52453, 53581, 54721, 55873, 57037, 58213, 59401 |
|
|
P12G,n = 1 + 12Tn-1 = 1 + 6 (n – 1)n = 1 + 6n² – 6n |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |