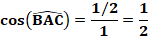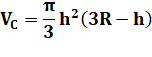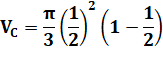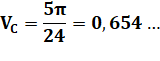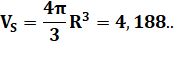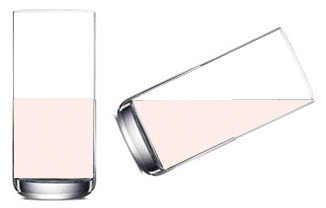
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ÉNIGMES
Débutants Vitesse	REMPLISSAGE				Glossaire Vitesse
INDEX Jeux et énigmes	Tonneau	Robinets	Travaux	Nénuphar
	Verre penché	Verres empilés
		Sommaire de cette page >>> Verre cylindrique >>> Verre sphérique

Énigme du verre penché

Cylindrique & Sphérique

Verre cylindrique: comment le remplir à moitié sans faire de mesure ?

Verre semi-sphérique à moitié plein: jusqu'où peut-on le pencher sans renverser une goutte ?

Devinette

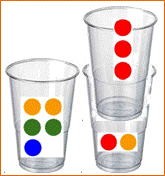
Comment passer de la situation du haut à celle du bas en un seul mouvement ?

Solution

VERRE cylindrique
Énigme Verre cylindrique à moitié plein. Comment s'en assurer ? Ou Le verre est plein, comment le remplir précisément à moitié sans effectuer de mesure ?
Solution Si le verre est penché jusqu'à ce que le niveau affleure le bord externe du verre, alors le verre contient la moitié de sa contenance. Il est aussi "à Commentaire Le cylindre est de révolution et le raisonnement sur la coupe plane est légitime.
Anglais

Voir Tonneau à moitié plein

Verre sphérique

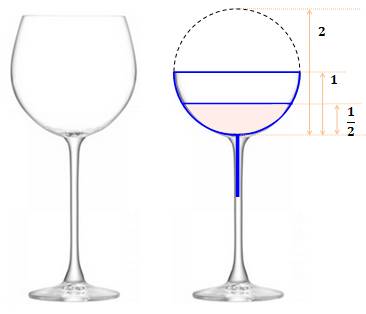
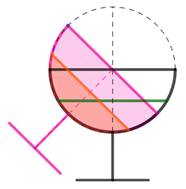
Énigme

Cette fois, nous disposons d'un verre ballon, comme celui de gauche, mais un peu arrangé pour les besoins de l'énigme.

Sa coupe est exactement une demi-sphère comme sur le dessin de droite.

Son rayon est d'une unité et il est rempli à moitié hauteur.

Jusqu'où peut-on pencher le verre sans renverser une seule goutte ? Quel est l'angle du pied avec la verticale ?

Approche

La sphère, comme le cylindre, présente une symétrie de révolution.

Un raisonnement dans le plan est légitime.

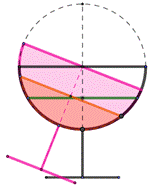
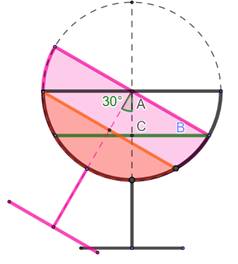
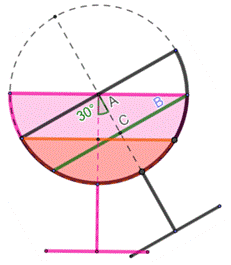
Solution

Il faut pencher le verre de 30°.

Le triangle ABC est rectangle en C et ses côtés mesurent 1 et 1/2

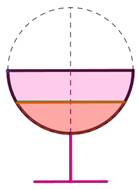
Bonus maths

Quel est le volume de liquide ?

On trouve:

Volume du liquide / Volume de la sphère = 15,6 %.

Volume de la calotte de hauteur h
Avec R = 1 et h = 1/2
Pour info: volume de la boule

Voir Brève 604

Devinette – Solution

Comment passer de la situation du haut à celle du bas en un seul mouvement ?

Prendre le deuxième verre et verser son contenu dans le cinquième, puis le remettre à sa place.

Retour / Autres énigmes

Résoudre cette énigme

2B + 1/2 B	= 15
B	= 6
J – 1/2J + 6	= 10
J	= 8
2R – 1/2R	= 6
R	= 4
1/2B + 1/2(R+B)(1/2J)
= 3 + 1/4(10) x 8	= 23

Voir Énigmes semblables

Résoudre cette énigme des trois verres

Énigme Trois verres et dix jetons (ou dix pièces). Placer un nombre impair de jetons dans chaque verre.	Solution Le nombre 10 est pair et la somme de trois nombres impairs est impaire. Solution impossible sans une astuce. Celle-ci consiste à mettre un gobelet dans un autre. Ils contiennent alors 5, 3, 5 jetons, des nombres impairs comme demandé.
Pour info: les huit partitions de 10 à trois termes (sur les 42 partitions du nombre 10): [3, 3, 4], [2, 4, 4], [2, 3, 5], [1, 4, 5], [2, 2, 6], [1, 3, 6], [1, 2, 7], [1, 1, 8] Chacune comporte un ou trois nombres pairs.

Voir Brève 593

Retour Suite	Nombre 0,5 Nénuphar Tonneau à moitié plein Énigmes avec le nombre 10
Voir	Bouteille – Calcul du volume Contenance – Bouteilles Cylindre Énigme des poules pondeuses Jeux et énigmes Mélange eau - pastis Progression géométrique Tonneau percé Verres à remettre dans le même sens les yeux bandés
Site
Cette page	http://villemin.gerard.free.fr/aJeux1/Temps/VerrePen.htm