|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Caractérisation des NOMBRES PREMIERS Quelles sont les
particularités des nombres par rapport aux nombres premiers. En maître règne bien
évidemment le théorème fondamental de l'arithmétique.
Voici d'autres relations remarquables |
|
|
|
|
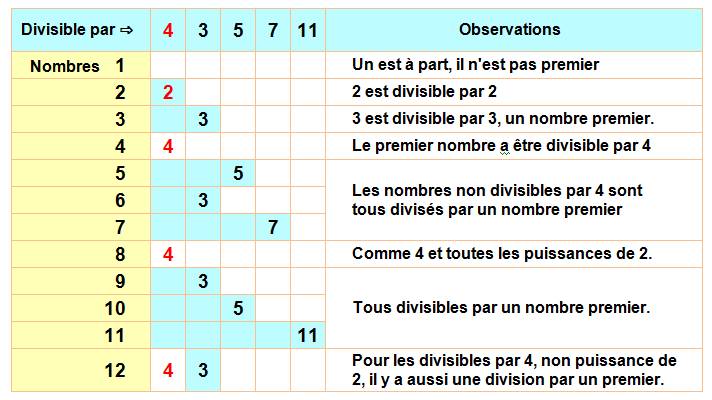
Tout nombre supérieur à 1 est divisible par 4 ou par
un nombre premier. Any integer greater than two is divisible either by 4 or by an odd
prime. |
|
|
|
|
|
|
|
Voir Tableau jusqu'à 50 / Un n'est pas
premier / Puissance de 2
|
|
||
|
Si le nombre est
premier |
n est divisible par un premier. |
|
|
Si le nombre est
composé |
Il est le produit de deux facteurs dont
l'un est premier (p1):
|
|
|
Si le facteur
premier est impair |
n est divisible par un premier. |
|
|
Si le facteur
premier est 2 |
Il considérer le second facteur comme un
nouveau nombre et recommencer cette procédure. |
|
|
|
||
|
Un nombre entier
est soit premier
soit composé |
||
|
S'il est premier Il
est divisible par un premier (lui-même). |
S'il est composé Il
est le produit de facteurs
premiers et notamment
d'un nombre par un facteur premier. |
|
|
n = premier FIN |
n = k . p Suite
|
|
|
Note:
de ce fait nous avons éliminé 2, 3, 5, 7 … |
Note: sauf dans le cas
où p = 2, le facteur premier
p est toujours impair |
|
|
|
|
|
|
Un nombre composé
est soit impair ou pair |
||
|
S'il est impair n
= k . p avec p impair. En
effet, on élimine p = 2 qui donnerait un nombre n pair,
contraire à l'hypothèse. Il
ne reste que p impair. Donc:
un nombre impair est toujours divisible par un premier impair. |
S'il est pair n
= 2k . p avec p = 2 ou p impair. Si
p est impair, il est divisible par un premier, selon ce qui est dit
ci-contre, à gauche. Si
p = 2, alors n = 4k. Donc:
un nombre pair est divisible par 4 ou par un premier. |
|
|
Impair divisible
par premier FIN |
Pair divisible par
4 ou par p Suite pour les
divisible par 4 |
|
|
|
|
|
|
Un nombre divisible
par 4 est une puissance de 2 ou non |
||
|
S'il est puissance de 2 n
= 2k Ce
nombre est toujours divisible par 2. Il
n'est pas premier. Il
fait donc partie de la catégorie des divisible par 4. Donc:
une puissance de 2 n'est pas divisible par un premier |
S'il n'est pas puissance de deux n
= 4k Ou
k est impair et on est ramené au cas déjà vu: k impair est divisible
par un premier. Ou
k est pair et il est de la forme 2k'
Cette
récurrence ne s'arête que si, en final le k"" est égal à 2, c'est à
dire si on a à faire à une puissance de 2. |
|
|
n = 2k
non divisible par un premier FIN |
Pair est une
puissance de 2 ou alors divisible par un premier FIN |
|
|
|
||
|
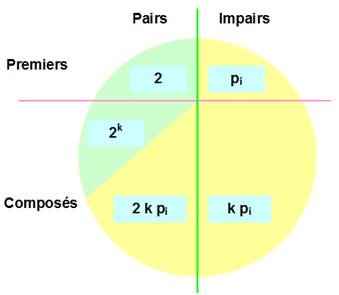
Le
cercle représente l'ensemble des nombres entiers. Tout
nombre est soit:
|
|
|
|
|
||||||||
|
0) |
n |
|
|
|
|
= k.p |
Tout
nombre est décomposable de façon unique en facteurs premiers. |
|
|
1) |
n |
|
|
= p |
ou |
= k.p |
Tout
nombre est premier ou divisible par un premier. |
|
|
2) |
n |
= 2 |
ou |
= pi |
ou |
= k.p |
Tout
nombre est premier pair (2) ou premier impair ou divisible par un premier. |
|
|
Nombre supérieur à 2 |
||||||||
|
3) |
n |
(>2) |
|
=
pi |
ou |
= k.p |
Tout
nombre supérieur à 2 est premier impair ou divisible par un premier. |
|
|
4) |
n |
(>2) |
|
= k.pi |
ou |
= 4t |
Tout
nombre supérieur à 2 est divisible par 4 ou par un premier impair. |
|
|
5) |
n |
(¹2a) |
|
= k.pi |
ou |
= 4t |
Tout
nombre supérieur à 2 est divisible par un nombre premier impair sauf les
puissances de 2. |
|
|
On se sert de telles propriétés pour limiter les cas d'études de
certains problèmes. Par exemple, pour le dernier
théorème de Fermat, on savait qu'il suffisait de traiter le cas de la
puissance 4 et ceux de puissance égale à un premier impair. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()