|
|||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 24 Formes polynomiales
divisibles par 24. Exemple Le
produit de trois nombres consécutifs (n – 1) n (n + 1) =
n3 – n dont
le central est impair, est divisible par
24. |
|
|
||
|
Le produit de quatre nombres
consécutifs est divisible par 24. En effet, parmi eux:
Le nombre résultant est un nombre polytope:
Quatre cinquièmes de ces nombres sont aussi divisible par 120. Ceux qui ne le sont pas
sont en 4 + 5k. |
|
|
|
|
||
|
n2 – 1 est divisible par 24 |
|
|
|
Autrement-dit: |
Le carré de tout nombre premier
supérieur à 3 est de la forme 24k + 1. |
|
Voir Table de ces nombres / Extension
/ Nombres carrés / Premiers
|
|
||
|
Outils utilisés |
|
|
|
|
sont impairs. |
|
|
|
est divisible par 8, car l'un l'est par 2 et
l'autre par 4. |
|
|
|
n p – 1 – 1 est divisible par p. |
|
|
Démonstration |
N = n2 – 1 = (n +
1) (n – 1) |
|
|
|
n est impair. |
|
|
|
Leur produit N est divisible par 8. |
|
|
|
N = n2 – 1 = n(p
– 1) – 1 avec p = 3 |
|
|
|
N est divisible par 3. |
|
|
|
N, divisible par 8 et par 3, est divisible par
24. |
|
|
Généralisation |
|
|
|
|
n est
impair non multiple de 3. |
|
|
|
n doit simplement
être premier avec 3. |
|
Voir Autre
démonstration
|
|
|
|
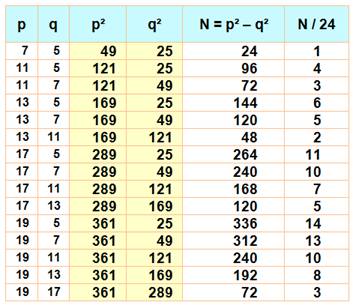
Les dernières
colonnes indiquent la raison Voir Factorielles tronquées / Nombres consécutifs impairs / Carré des impairs moins
un Explications
|
|
Voir Divisibilité par 24
|
|
||
|
Théorème p² – q² est divisible par 24 pour tout p et q premier > 4 Démonstration
p²
= 24k +1 q²
= 24k' + 1
p²
- q² = 24 (k – k') |
|
|
|
|
||
|
|
m = 2 . 7n + 3 . 5n - 5 |
|
|
Démonstration par induction |
||
|
|
2 . 7 + 3 . 5 – 5 = 14 + 15 – 5 = 24 |
|
|
|
m' = 2 . 7k+1
+ 3 . 5k+1 – 5 = 2 . 7k . 7 + 3 . 5k
. 5 – 5 = 7 ( 2 . 7k
+ 3 . 5k – 5) – 6 . 5k + 30 = 7m – 6 . 5k
+ 30 |
|
|
(La barre verticale veut dire divise) |
m' = 7m Or 24 | m |
|
|
Le premier terme de m' est divisible par 24
selon notre hypothèse. Il s'agit de démontrer que le deuxième
terme est divisible par 24. |
6 . 5k + 30 = 30 (5k-1
– 1) = 30 (5 – 1) (5k-2 + 5k-3
+ … + 5 + 1) = 30 x 4 (5k-2 + 5k-3 +
… + 5 + 1) Or 24 | (30 x 4) |
|
|
Exemples |
|
|
|
Variante de la démonstration |
(plus
d'explications) |
|
|
Validation du point de départ |
|
|
|
Le théorème est donc vrai pour n = 1. |
f(1) |
=
2 . 7 + 3 . 5 - 5 |
|
Validation de la récurrence |
|
|
|
|
f(n) |
=
24 .k |
|
On
essaie de dégager des exposants identiques à ceux de f(n). |
f(n+1) |
=
2 . 7 (n+1) + 3 . 5 (n+1) - 5 =
7 .2 . 7 n + 5 . 3 . 5 n - 5 |
|
|
7 f(n) - f(n+1) |
=
- 7 .2.7 n - 5 . 3.5 n + 5 +
7 . 2.7 n + 7 . 3.5 n - 7 . 5 = 2 . 3 . 5 n - 6 . 5 = 6 . 5 n - 6 . 5 |
|
|
|
= 6 . 5 . 5 n-1 - 6 . 5 = 30 (5 n-1 - 1) |
|
|
7 f(1) - f(2) 7 . 24 - f(2) f(2) |
=
30 (1 - 1) =
0 =
24 . 7 |
|
|
7 f(n) - f(n+1) 5
n-1 - 1 |
=
30 (5 n-1 - 1) =
(5-1) (5n-2 + 5n-3 +…+ 5 + 1) =
4 . h |
|
|
7 f(n) - f(n+1) |
=
30 (5 n-1 - 1) =
30 . 4 . h =
120 . h =
24 . 5 . h |
|
|
f(n) f(n+1) |
=
24 . k =
24 . h |
|
Conclusion |
|
|
|
Si
la propriété est vraie pour une valeur (n), elle est vraie pour la
valeur suivante (n + 1) |
||
|
|
||
|
Théorème Le produit de trois nombres
consécutifs dont le central est impair est divisible par 24. Démonstration par induction >>> |
m = n (n² – 1) = (n – 1) n (n + 1) est divisible par 24 si n est impair. |
|
|
|
m = 0 et 24 | 0 Même si ce résultat est trivial. |
|
|
|
m = (2k – 2) (2k – 1) (2k) m' = 2k (2k + 1) (2k + 2) |
|
|
|
m' = 2k (2k + 1) (2k + 2) = (2k – 2 + 4) (2k – 1 + 2) 2k |
|
|
Chaque
terme est divisible par 24. La
somme est divisible par 24. CQFD. |
= { (2k – 2) (2k – 1) + (2k – 2) 2 + 4 (2k
– 1) + 8) } 2k = m + (4k - 4 + 8k – 4 + 8) 2k = m + (12k) 2k = m + 24 k² |
|
|
Exemples |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi24.htm |
![]()