NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	Distances			Glossaire Géométrie
INDEX Graphes Géométrie Topologie Dénombrement	Distance	Médiatrice	Diagramme de Voronoï
	Lycée et +	Sommaire de cette page >>> Approche >>> Construction >>> Définition et interprétation >>> Voronoï et Delaunay >>> Propriétés >>> Historique et applications >>> Anglais		Source Voro++

Faites un double-clic pour un retour en haut de page

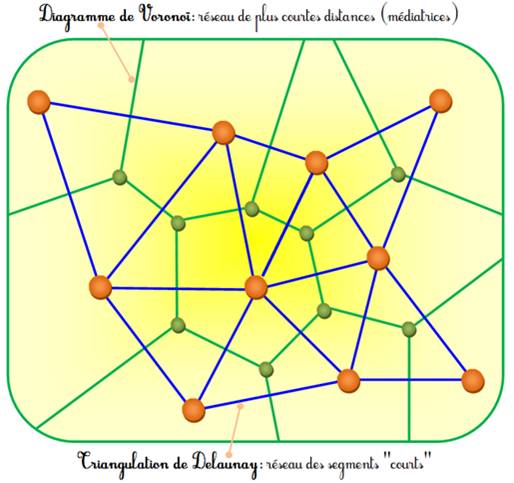
Diagramme de VORONOÏ

et partition de Delaunay

(réseau de Dirichlet ou polygone de Thiessen)

L'offre de cinémas est importante dans ma région. Mais quelle est la salle la plus proche? Comment gérer les situations de collisions potentielles en navigation maritime? Et bien d'autres applications >>>

Ces outils, qui traitent des réseaux de points, sont fondamentaux en géométrie algorithmique, c'est-à-dire traitée par ordinateurs.

Trois domaines d'investigations:

Études de leurs propriétés géométriques et même statistiques;

Construction des diagrammes par ordinateur; et

Application à la modélisation des phénomènes.

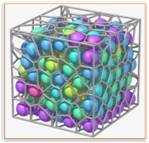
Le cas où le réseau de points dans l'espace est régulier est d'un grand intérêt pour l'étude de la cristallographie

Mais avant tout, c'est un bon sujet de découverte et d'amusement, abordable avec un bagage élémentaire en géométrie.

Anglais: Voronoi diagrams or Voronoi tessallations or Dirichlet's tessellation

Georgy Voronoï ou Voronoy (1868-1908)

Mathématicien né en Ukraine et mort en Pologne.

Travaux sur: racines des équations du troisième degré, nombres algébriques, nombres de Bernoulli, algorithmes pour les fractions continues, la géométrie des nombres, les fonctions transcendantes.

Ses diagrammes sont utilisés dans l'analyse des données distribuées spatialement. Ils sont à la base de la démonstration de la conjecture de Kepler sur l'empilement des sphères.

Boris Delone ou Delaunay et Waclaw Sierpinski furent ses élèves.

Voir Contemporains

Approche
Deux cinémas, l'un en A et l'autre en B. Là où je suis en ce moment, j'ai plutôt intérêt à me diriger vers A (si on y joue le film que je souhaite voir). La frontière de choix passe par la médiatrice MM' de AB. Chaque fois que je me trouve sur la médiatrice je suis à égale distance de chacun des points A et B. Un troisième cinéma s'est implanté dans la région. Nous avons trois zones délimitées par les trois médiatrices. Celles-ci, pour tout triangle, sont concourantes en un point. 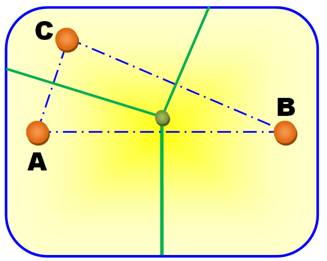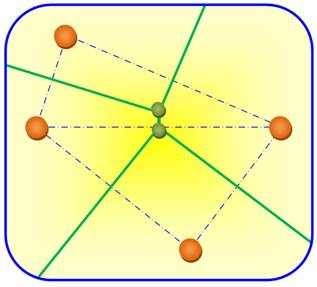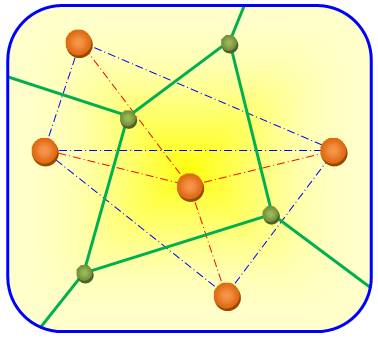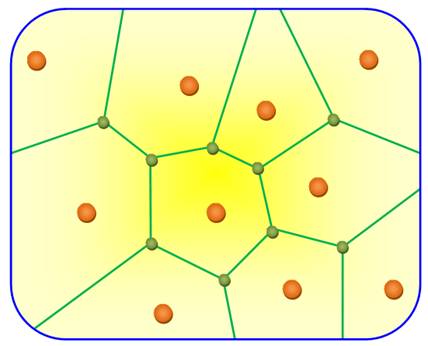Les lignes vertes forment le diagramme de Voronoï et le point de concours est un point de Voronoï. Les points A, B et C sont appelés les germes et les sites. Tous les points situés dans une zone (un polygone convexe) de Voronoï sont plus proches de son site que de tous les autres sites. Exemple: si les sites sont des garages et si je suis en panne, j'ai intérêt à me diriger vers le garage de la zone où je me trouve, c'est le plus proche. Avec quatre points la construction n'est pas plus compliquée. Les médiatrices s'arrêtent à l'intersection avec une autre.

Construction
On commence par un point central et les segments le liant aux autres sites proches (en rouge). On trace les médiatrices de tous ces segments. Elles forment un polygone autour du point considéré. On termine en traçant les médiatrices des segments formés par les couples proches. Chacune rejoint l'un des sommets du polygone (points de Voronoï). Exemple de diagramme de Voronoï à dix points. En comptant les frontières extérieures, chaque point (site) est à l'intérieur d'un polygone convexe. Tous les points de ce polygone sont plus proches du point interne que de tous les autres points. Il s'agit d'un réseau en nid d'abeille irrégulier.

Définition et interprétation

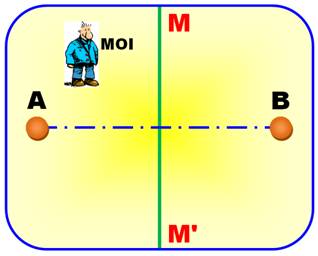
Un diagramme de Voronoï s'applique à un ensemble de points E d'un plan, appelés sites ou germes. Le diagramme est un réseau comportant des polygones convexes. Chacun délimite la zone dans laquelle tout point est plus proche de son germe que de tous les autres germes. Voir formulation

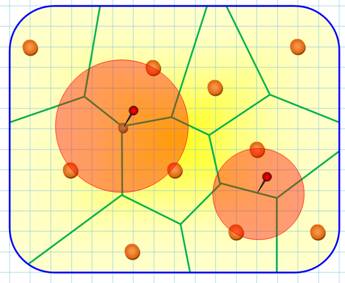
Le terme "germe" vient d'une vision dynamique de formation de ces diagrammes. Imaginez un cercle croissant à une vitesse constante, attaché à chaque point. Quand deux cercles se rencontrent la frontière forme une frontière linéaire, médiatrice des deux germes responsables. La croissance arrivée à son terme forme une partition du plan dite décomposition de Voronoï. Chaque région est l'ensemble des points les plus proches d'un germe.

Diagramme de Voronoï et partition de Delaunay
Vous avez déjà remarquez que pour engendrer un diagramme de Voronoï certaines médiatrices sont utilisée et pas d'autres. Dit-autrement, certaines connexions entre les points sont mises en jeu et pas d'autres. Les points trop lointains n'ont pas d'influence. Les segments utiles forment une triangulation ou partition du plan dite de Delaunay. En mécanique une structure en triangulation de Delaunay est le maillage le plus efficace. Elle minimise les carrés des aires des triangles.

Propriétés

Géométriques Un point de Voronoï est de degré 3. Un raisonnement impliquant la relation d'Euler montre que: quantité d'arêtes max. = 3n – 6; quantité de sommets max. = 2n – 5; et chaque arête appartient à exactement deux régions. Chaque sommet et le centre d'un cercle vide passant par trois sites. Chaque point sur une arête est le centre d'un cercle vide passant par deux sites. Générales Les deux représentations (Voronoï et Delaunay) sont des graphes planaires (qui ne se croisent pas dans le plan). L'un est le dual de l'autre. Chacun représente la même réalité. En géométrie, ce diagramme peut servir à trouver le plus grand cercle vide dans une région de Voronoï. L'algorithme de Steven Fortune (1987) engendre le diagramme par croissance de paraboles. Il a été démontré comme asymptotiquement optimum. Voir exemple animé et code en Fortune's algorithm – Wikipedia Le diagramme de Voronoï classique utilise la notion classique de distance (euclidienne) où le théorème de Pythagore s'applique. Cette notion peut être généralisée en adoptant d'autres définitions de la distance, comme, par exemple, le suivi de chemin à angle droit (comme les rues de Manhattan). Une autre de voie de généralisation consiste à s'intéresser à un groupe de points proche d'un point donné. Les diagrammes de Voronoï sont de bons candidats pour l'étude de la géométrie algorithmique. Nombreux sites sur Internet avec le détail du code.

Voir Graphe et le problème des quatre couleurs

Historique et applications

Chronologie

1644 – René Descartes utilise de tels diagrammes pour représenter l'espace du système solaire.

1840 – Gauss observe le premier un rapport avec les formes quadratiques.

1850 – Dirichlet exploite l'observation de Gauss et démontre l'unicité de la réduction des formes quadratiques.

1907 – Voronoï les utilise en les généralisant à plus de deux dimensions.

1934 – Delaunay introduit sa partition pour des réseaux irréguliers; méthode de croissance du cercle vide.

1854 – Épidémie de choléra à Londres. Cet outil permit à John Snow de mettre en évidence un lieu infecté fautif, en fait une pompe dans le quartier de Soho.

v. 1980 – Application aux polytopes (hyperpolyèdres).

v. 2000 – Application modélisation des surfaces, à leur échantillonnage. Comme les splines le font aussi.

Depuis: utilisation en images calculées, épidémiologie, géophysique, météorologie, navigation, robotique …

Applications typiques

borne d'appel de secours,

cristallographie,

croissance de cellules végétales,

empilement des sphères

espace occupés par les arbres dans la forêt,

partition du cosmos selon étoiles et galaxies,

évolution de cellules cancéreuses,

prévisions climatiques,

proximités entre atomes,

relais de communication,

restaurants le plus proche,

taches sur la peau (girafes),

zones de collision potentielle en navigation,

zones maritimes exclusives (ZEE)

etc.

Ces outils, qui traitent des réseaux de points, sont fondamentaux en géométrie algorithmique, c'est-à-dire traitée par ordinateurs: images calculées, conception assistée par ordinateur, reconnaissance de caractères, recherche opérationnelle …

English corner

The Voronoi diagram is one of the most fundamental data structures in computational geometry. Given some number of points in the plane, their Voronoi diagram divides the plane according to the nearest-neighbor rule: each point is associated with the region of the plane closest to it. Definition of the Voronoi diagram: Let S denote a set of n points, called (sites) in the plane. For two distinct sites p, q S, the dominant of p over q is defined as the subset of the plane being at least as close to p as to q. Formally, with delta denoting the euclidean distance: The planar Voronoi diagram and the Delaunay triangulation are duals in a graph theoretical sense. Voronoi vertices correspond to Delaunay triangles.

Suite	Empilement des sphères Densité des disques Hypersphère et Univers	Nombres de Delannoy Problème de Kakeya Graphe – Index
Voir	Construction à la règle et au compas Énigmes classiques Géométrie – Index Jeux divers – Index Le cube Les nombres cubes	Les trois filles Pliages Polyèdres Polytopes Quadrature du cercle
Sites	Reconstruire des surfaces pour l'imagerie – Interstices: explications et animations interactives Spherical Voronoi diagram de jason Davies - Interactif. Voir son Voronoï des aéroports Un petit peu de géométrie algorithmique – Frank Hétroy – Ensimag (pdf, supérieur)) Voronoi Diagrams – A survey of a fundamental geometric data structure – Franz Aurenhammer – 1999 – Revue de tous les domaines d'applications (anglais, pdf) Voronoi diagrams (Computational lecture) – Introduction et explication complète de l'algorithme de construction (anglais, pdf) Voronoi Diagrams – Indian Statistical Institute – Explication des algorithmes de construction (anglais, pdf)
Cette page	http://villemin.gerard.free.fr/Geometri/Voronoi.htm