|
Dimensions
supérieures
(à 4)
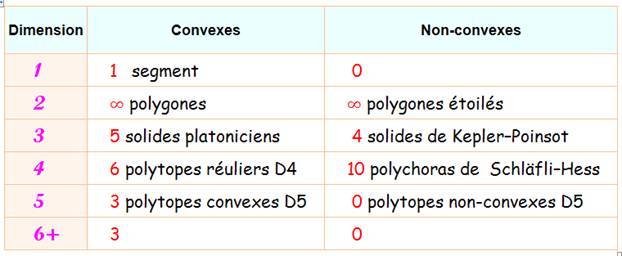
En dimension cinq ou plus, il
n'existe que trois polytopes convexes réguliers.
Polytope
spécial
Représentation du groupe de Lie E8
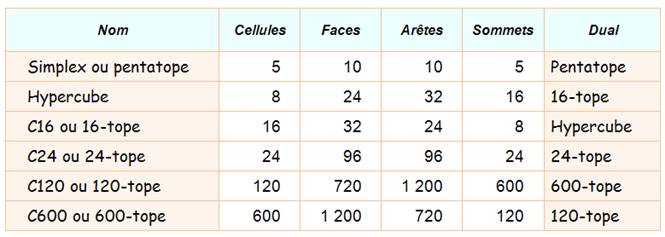
Familles
de polytopes
Voici un récapitulatif des
plus simples d'entre eux:
Suite en Liste des polytopes
 La famille comporte les sous-familles des simplexes
réguliers, famille généralisant la notion de triangle (D2) et du
tétraèdre (D3); en D4, nous aurons le pentachore.
Un simplexe est l'enveloppe convexe d'un ensemble de (n+1) points. Son nom
vient du fait qu'il s'agit de l'objet clos le plus simple enveloppant un
groupe de points donnés.
Par
exemple, un simplexe de dimension 5 (D5),
aussi nommé hexatère, possède: 6
sommets, 15 arêtes, 20 faces triangles, 15 cellules tétraédriques et 6
"faces" pentachores. L'hexatère est l'un des 19 polytères
uniformes.
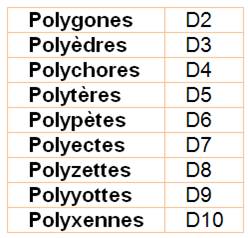
Selon la dimension, ces
objets prennent effectivement des noms dont la
racine est issue du grec:
Les polytopes sont une source
inépuisable de découvertes. Je vous laisse
les découvrir sur Internet. Laissez-vous guider sur Wikipédia français
et également anglais.
|
