|
|||||||||||||||||||||||||||||
|
LES
TROIS FILLES Le problème du recenseur (The Census-Taker Problem) Énigmes qui semblent insolubles. Finalement pas si compliquée avec un
peu de méthode. |
|
Cette
énigme remonte à la seconde Guerre Mondiale en provenance du MIT. Depuis, d'autres énigmes du même genre ont fleuries lesquelles ont soulevé des interrogations en théories des nombres |
Les nombres particuliers concernés par de type d'énigme sont appelés les nombres du recenseur (Census-Taker Number: CTN) |
|
|
||
|
Deux vieux amis se
rencontrent dans la rue ; ils ne se sont pas vus depuis très longtemps. L'un d'eux annonce à son ami
qu'il a désormais 3 filles. Curieux, l'autre lui demande
leurs âges. |
||
|
Et l'homme répond ainsi: |
Si
on multiplie leurs trois âges, on obtient 36. |
|
|
L'autre, perplexe, lui rétorque: |
Je
ne peux pas déterminer leurs âges avec si peu d'information. |
|
|
Alors le père de famille lui dit : |
La
somme de leur âges est égale au numéro de la maison d'en face. |
|
|
L'autre regarde et déclare : |
Non,
je ne peux toujours pas déterminer leurs âges. |
|
|
Alors, l'homme regarde son ami dans les
yeux et dit : |
L'aînée
est blonde... |
|
|
Le visage de son ami s'éclaire alors et il
s'écrit : |
Ça
y est ! Maintenant je sais. |
|
|
Et vous, savez-vous l'âge
des filles ? P.S. Il n'y a aucun jeu de mot, tout cela est
parfaitement logique et un enfant de 10 ans a les connaissances pour résoudre
ce problème. |
||
|
La version anglaise du Census-Taker problem A census-taker approaches a house and asks the
woman who answers the door "How
many children do you have, and what are their ages?" The woman replies "I have three children, the product of their ages is 36, the sum
of their ages is equal to the address of the house next door." The census taker walks next door, comes back and
says "I need more
information." The woman replies "I have to go, my oldest child is sleeping upstairs." Census taker then says "Thank you, I now have everything I need." Autre version A census taker knocks on a door. A mother
answers. The census taker says, “I need to know the number of children you have, and their ages.” The woman responds in puzzle-ese, “I have three daughters, the product of
their ages is 36, and the sum of their ages is equal to the house number next
door.” The census taker, who never wastes questions,
computes for a while and then asks, “Does
your oldest daughter love dogs?” The mother answers affirmatively. The census
taker says, “Thank you. I now know the
ages.” What are the ages of the children? |
||
|
Premier indice |
|
|
|
Si on multiplie les 3 âges,
on obtient 36. Quels sont les trois nombres
dont la multiplication donne 36 ? Il y a huit solutions dont
trois avec des jumeaux (en rouge) . |
1
x 1 x 36 |
|
|
Deuxième indice |
|
|
|
La somme de leur âges est
égale au numéro de la maison d'en face. Bien sûr, vous ne voyez pas
le numéro de la maison d'en face, mais calculons les sommes. Si l'ami ne trouve pas l'âge
des filles c'est qu'ils sont en face du numéro 13, le numéro répété deux
fois, créant une ambiguïté. Sinon, avec un seul numéro, il aurait eu la
solution ! C'est pourquoi il répond, je ne peux pas encore trouver la
solution. En effet, il reste encore 2
solutions possibles. |
1 + 1 + 36
= 38 |
|
|
Troisième indice |
|
|
|
L'aînée est blonde. Voici un indice qui va
permettre une nouvelle déduction Dans le triplé: 1 an, 6 ans
et 6 ans, il n'y a deux aînées: ce qui n'est pas possible puisqu'il y a une
aînée seulement. |
La solution est
donc:
|
|
|
|
||
|
Dialogue entre le capitaine et son second |
||
|
Capitaine |
Son second |
|
|
J'ai rencontré 3
filles et le produit de leurs âges est 2450. |
Je ne peux pas déterminer leurs âges avec
si peu d'information. |
|
|
J'ajoute que la
somme de leurs âges est égale au double du mien. |
Je ne peux toujours pas ! |
|
|
Et enfin, la plus
âgée est au moins aussi vieille que moi. |
Ca y est !!! Maintenant je sais. |
|
|
Quel
est l'âge du capitaine ? |
||
|
Solution |
|
|
|
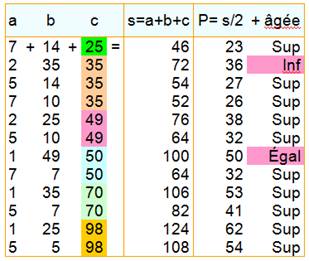
Les diviseurs de 2450 sont: 1, 2, 5,
7, 10, 14, 25, 35, 49, 50, 70, 98, 175, 245, 350,
490, 1225, 2450. On note: a, b, et c l'âge de chaque
fille. Quels sont les groupes de trois diviseurs qui donnent un
produit de 2450? Voir recherche des produits ci-dessous. On observe que l'âge de l'aînée est unique dans le seul
premier cas: 7, 14, 25. Voyons maintenant l'âge du capitaine: P = (a+b+c) /2. Et indiquons les cas pour lesquels la fille aînée est
au moins aussi âgée que le capitaine c'est-à-dire: son âge est supérieur ou
égal à celui du capitaine. En disant "et enfin", le
capitaine indique que le seul indice qui suit doit donner la solution. Or
dans une majorité des cas, il y a indécision. Par
exemple avec 35 ans, le
capitaine peut avoir soit 26 ou 27 ans Il ne faut donc ne prendre que les cas sans confusion.
Il n'en reste qu'un seul. 7, 14 & 25 pour les filles et 23 pour le capitaine |
|
|
Voir Nombres recenseurs
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
