|
Édition du: 24/08/2022 |
|
INDEX |
TRIANGLES Éléments remarquables |
||||
|
Éléments remarquables – Index |
|||||
![]()
|
POINTS CARACTÉRISTIQUES du Triangle Nombres de Kimberling Kimberling Numbers
Clark
Kimberling (né en 1942), mathématicien et musicien (religieux) américain
(Illinois). Créateur de Encyclopedia of Triangle Centers (ETC). |
||
|
|
Sommaire de cette page >>>
Approche – Les quatre points classiques >>>
Points remarquables et nombres de Kimberling |
Débutants Glossaire |
|
Les quatre premiers X(1)
Centre du cercle inscrit X(2)
Centre de gravité X(3)
Centre du cercle circonscrit X(4)
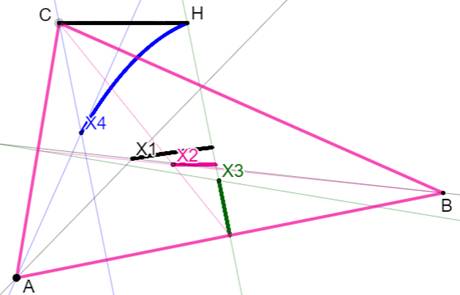
Orthocentre Figure Les quatre points sont positionnés dans le
triangle ABC. On montre la trace de ces quatre points lorsque
le sommet C se déplace sur le segment CH. Avec C en H, le triangle ABC est isocèle.
Les quatre points sont alignés. Ils seraient confondus avec un triangle équilatéral. |
Trace des points remarquables selon
le déplacement du point C
|
|
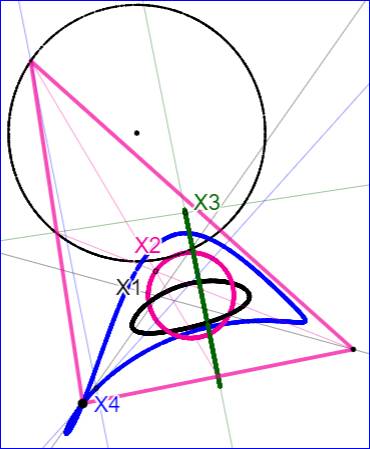
Trace des quatre points avec le point C parcourant un cercle
|
POINTS – Points (Triangle centers) & Nombres de Kimberling (K) |
||||
|
Rubrique |
K |
Nom du point |
Concerne |
Lien |
|
Sur triangle |
/ |
Milieux des côtés |
Pieds des médianes et des
médiatrices. |
|
|
/ |
Exmédian |
Sommets des segments
exmédians. Points de rencontre des parallèles aux côtés passant par le sommet
opposé. |
||
|
Classiques |
1 |
Centre du cercle inscrit Incenter |
PC (Point de
concours) des Bissectrices. |
|
|
|
2 |
Centre de gravité Gravity center / Centroid |
PC des Médianes. Isobarycentre des sommets. |
|
|
|
3 |
Centre du cercle circonscrit Circumcenter |
PC des Médiatrices. |
|
|
|
4 |
Orthocentre Orthocenter |
PC des Hauteurs. |
|
|
|
(1) |
Centres des cercles exinscrits Excenter |
PC d'une Bissectrice
intérieure et deux Bissectrices extérieures. Trois points. |
|
|
Spéciaux |
8 |
Nagel |
PC des droites reliant les
points de tangence des cercles exinscrits aux sommets du triangle. |
|
|
|
9 |
Mittenpunkt |
PC des droites reliant les
centres des trois cercles exinscrits aux milieux respectifs des côtés du
triangle. |
|
|
|
10 |
Spieker |
Centre du cercle inscrit au
triangle médian Centre de masse du périmètre
du triangle |
|
|
|
181 |
Appollonius |
Le cercle d'Apollonius est
le cercle circonscrit aux trois cercles exinscrits. Le point d'Apollonius est le
PC des droites reliant les points de tangence aux sommets opposés du
triangle. |
|
|
Céviennes |
/ |
Céva |
Théorème de Céva. |
|
|
|
76 |
Brocard |
Deux points de Brocard et un
troisième X(76) |
|
|
|
6 |
Lemoine Symmedian point |
PC des symédianes (symétriques des médianes par
rapport aux bissectrices). |
|
|
Conjugués |
/ |
Terquem |
Deux faisceaux de céviennes. |
|
|
|
/ |
Isotomique |
Deux faisceaux de céviennes et symétrie par
rapport aux milieux des côtés. |
|
|
|
7 |
Gergonne |
PC des céviennes des points
de tangence du cercle inscrit. |
|
|
|
14 |
Isogonaux |
Points en rapport à un point
P et les bissectrices des angles du triangle. |
|
|
|
15 16 |
Isodynamique |
Centre d'inversion qui
transforme le triangle en triangle équilatéral. |
|
|
Construction |
12 |
Fermat (Steiner, Torricelli) |
Triangles équilatéraux sur
les côtés. |
|
|
|
5 |
Euler Nine-point center |
Points milieux entre sommets
et orthocentre. Situés sur le cercle des neuf points. |
|
|
|
11 |
Feuerbach |
Cercles tangents. |
|
|
|
22 |
Exeter |
Droites de jonction dans le
triangle circonscrit au cercle circonscrit du triangle. |
|
|
|
485 |
Vecten |
PC des droites joignant les
centres des carrés apposés aux côtés aux sommets opposés du triangle. |
|
|
|
17 18 |
Napoléon |
PC des droites joignant les
centres des triangles équilatéraux apposés aux côtés aux sommets opposés du
triangle. |
|
|
|
501 |
Miquel |
PC de trois cercles. |
|
|
|
99 |
Steiner |
Point en relation avec le
cercle circonscrit et la symédiane. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Remarqua/Kimberli.htm
|