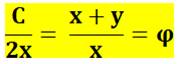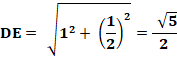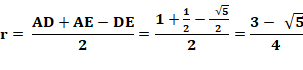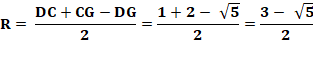Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 15/11/2024 M'écrire Brèves de Maths

INDEX Suite de Fibonacci et nombre d'or Défis en géométrie Géométrie	Nombre d'or
	Index	Introduction	Proportion	Construction
	Géométrie	Étoile	Aire Phi	Cercle
	Carré + Cercles

Faites un double-clic pour un retour en haut de page

Nombre d'or dans un carré avec deux cercles tangents Une jolie propriété avec le nombre d'or caché dans le carré accompagné de deux cercles inscrits, et une démonstration finalement pas si simple à trouver ! On trouvera une introduction à ce sujet en: deux cercles dans un carré – Défi
	Sommaire de cette page >>> Nombre d'or improbable >>> Démonstration	Débutants Nombre d'or Glossaire Nombre d'or

Nombre d'or improbable		haut
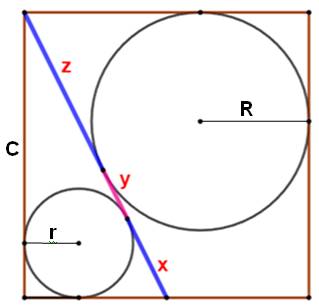
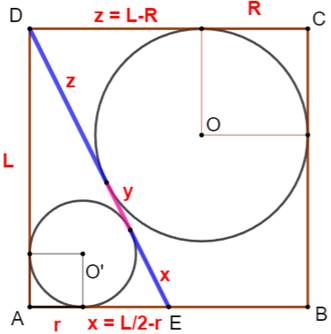
Construction Un carré et une semi diagonale joignant un sommet au milieu du côté opposé. Les deux cercles inscrits dans les espaces créés. Les points de tangence partage la semi-diagonale en trois segments de longueur x, t et z Propriété On a aussi: y = r = R/2 x + y = C/2	Figure

Voir Brève 59-1162

Démonstration		haut
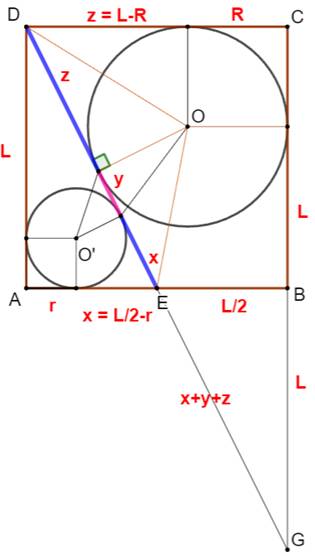
Pistes des tangentes On choisit L = 1, ce qui ne retire rien à la généralité. Les segments de tangentes issues d'un même point ont même longueur. Ce qui permet de noter: x = L/2 – r = 1/2 – r et z = L – R = 1 – R Longueur de l'hypoténuse DE (avec Pythagore). Rayon du petit cercle Rayon du cercle inscrit dans un triangle rectangle: Rayon du grand cercle Prolongeons le trapèze rectangle DCBE pour en faire un triangle rectangle DCG. Avec DC parallèle à EB et DC = 2 EB, alors: BG = BC et EG = ED. Rayon du cercle inscrit dans ce triangle rectangle: Soit: R = 2r Calcul de la proportion dorée	Mise en évidence des tangentes Construction du triangle rectangle

Voir Brève 59-1162

Haut de page (ou double-clic)

Suite	Deux cercles dans un carré – Calcul des rayons Deux cercles dans un carré – Divers défis Géométrie et nombre d'or Valeurs du nombre d'or Construction Trigonométrie
Voir	Cercle Constante Pi Constantes Mathématiques Construction géométrique des nombres Série du type Fibonacci et cousins
Sites	Golden ratio in geometry – Cut the Knot Golden ratio by compass only – Cut the Knot Geometric construction of Phi in circles – The Golden Number
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrCarr.htm