|
|||||||||||||||||||||||||||||||||||
![]()
|
|
|||
|
Nombres
consécutifs dont les sommes des chiffres (SC) sont divisibles par des nombres
consécutifs ou identiques. Liste: n, n+1, SC(n), SC(n+1), [d1, d2] Exemple: SC(189)
= 18 divisible par 6 et SC(190) = 10 divisible par 5. Les suivants (en rose) du même type);
espacés de 90. |
|||
|
8, 9, 8,
9, [4, 3] 17, 18, 8,
9, [4, 3] 26, 27, 8,
9, [4, 3] 35, 36, 8,
9, [4, 3] 44, 45, 8,
9, [4, 3] 53, 54, 8,
9, [4, 3] 62, 63, 8,
9, [4, 3] 71, 72, 8,
9, [4, 3] 78, 79, 15, 16, [3, 4] 79, 80,
16, 8, [4, 4] 80, 81, 8, 9, [4, 3] 87, 88,
15, 16, [3, 4] 96, 97,
15, 16, [3, 4] 107, 108,
8, 9, [4, 3] 116, 117,
8, 9, [4, 3] 125, 126,
8, 9, [4, 3] 134, 135,
8, 9, [4, 3] 143, 144,
8, 9, [4, 3] 152, 153,
8, 9, [4, 3] 161, 162,
8, 9, [4, 3] 168, 169, 15, 16, [3, 4] 169,
170, 16, 8, [4, 4] 170, 171, 8, 9, [4, 3] 177, 178,
15, 16, [3, 4] 186, 187,
15, 16, [3, 4] |
189,
190, 18, 10, [6, 5] 195, 196,
15, 16, [3, 4] 206, 207,
8, 9, [4, 3] 215, 216,
8, 9, [4, 3] 224, 225,
8, 9, [4, 3] 233, 234,
8, 9, [4, 3] 242, 243,
8, 9, [4, 3] 251, 252,
8, 9, [4, 3] 258, 259,
15, 16, [3, 4] 259, 260,
16, 8, [4, 4] 260, 261,
8, 9, [4, 3] 267, 268,
15, 16, [3, 4] 276, 277,
15, 16, [3, 4] 279,
280, 18, 10, [6, 5] 285, 286, 15,
16, [3, 4] 294, 295,
15, 16, [3, 4] 305, 306,
8, 9, [4, 3] 314, 315,
8, 9, [4, 3] 323, 324,
8, 9, [4, 3] 332, 333,
8, 9, [4, 3] 341, 342,
8, 9, [4, 3] 348, 349,
15, 16, [3, 4] 349, 350,
16, 8, [4, 4] 350, 351,
8, 9, [4, 3] 357, 358,
15, 16, [3, 4] |
366, 367,
15, 16, [3, 4] 369,
370, 18, 10, [6, 5] 375, 376,
15, 16, [3, 4] 384, 385,
15, 16, [3, 4] 389, 390,
20, 12, [4, 3] 393, 394,
15, 16, [3, 4] 398, 399,
20, 21, [4, 3] 404, 405,
8, 9, [4, 3] 413, 414,
8, 9, [4, 3] 422, 423,
8, 9, [4, 3] 431, 432, 8,
9, [4, 3] 438, 439,
15, 16, [3, 4] 439, 440,
16, 8, [4, 4] 440, 441,
8, 9, [4, 3] 447, 448,
15, 16, [3, 4] 456, 457,
15, 16, [3, 4] 459,
460, 18, 10, [6, 5] 465, 466,
15, 16, [3, 4] 474, 475,
15, 16, [3, 4] 479, 480,
20, 12, [4, 3] 483, 484,
15, 16, [3, 4] 488, 489,
20, 21, [4, 3] 492, 493,
15, 16, [3, 4] 497, 498,
20, 21, [4, 3] |
|
|
Cas
6, 5 189, 190,
18, 10, [6, 5] 279, 280,
18, 10, [6, 5] 369, 370,
18, 10, [6, 5] 459, 460,
18, 10, [6, 5] 549, 550,
18, 10, [6, 5] 639, 640,
18, 10, [6, 5] 729, 730, 18,
10, [6, 5] 819, 820,
18, 10, [6, 5] 909, 910,
18, 10, [6, 5] 1089,
1090, 18, 10, [6, 5] 1179,
1180, 18, 10, [6, 5] 1269,
1270, 18, 10, [6, 5] |
Cas
10, 11 (seul après 6, 5) 4989,
4990, 30, 22, [10, 11] 5889,
5890, 30, 22, [10, 11] 5979,
5980, 30, 22, [10, 11] 6789,
6790, 30, 22, [10, 11] 6879,
6880, 30, 22, [10, 11] 6969,
6970, 30, 22, [10, 11] 7689,
7690, 30, 22, [10, 11] 7779,
7780, 30, 22, [10, 11] 7869,
7870, 30, 22, [10, 11] 7959,
7960, 30, 22, [10, 11] 8589,
8590, 30, 22, [10, 11] 8679, 8680,
30, 22, [10, 11] 8769,
8770, 30, 22, [10, 11] 8859,
8860, 30, 22, [10, 11] 8949,
8950, 30, 22, [10, 11] 9489,
9490, 30, 22, [10, 11] 9579,
9580, 30, 22, [10, 11] 9669,
9670, 30, 22, [10, 11] 9759,
9760, 30, 22, [10, 11] 9849,
9850, 30, 22, [10, 11] 9939,
9940, 30, 22, [10, 11] |
Rienau-delà Cas7,
7 69999,
70000, 42, 7, 159999,
160000, 42, 7, 249999,
250000, 42, 7, 339999,
340000, 42, 7, 429999,
430000, 42, 7, 519999,
520000, 42, 7, 589999,
590000, 49, 14, 609999,
610000, 42, 7, 679999,
680000, 49, 14, 769999,
770000, 49, 14, 859999,
860000, 49, 14, 949999,
950000, 49, 14, |
|
|
|
|
|
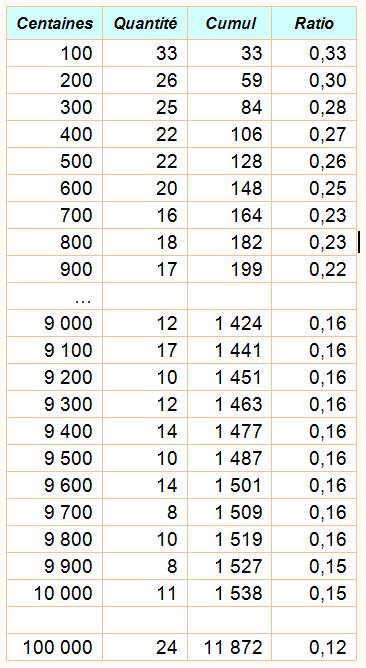
On donne la quantité de nombres harshads
par tranche de centaines. Avec le cumul, on calcule le ratio nombres harshads sur
nombres naturels.
|
|
|
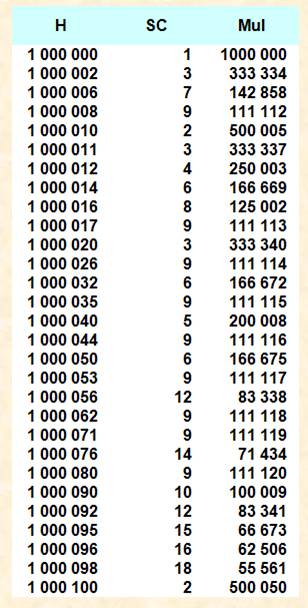
Liste de grands nombres HARSHADS 1 000 000 < N < 1000 100 |
|
|
En présence de zéros, quantité appréciable de nombres harshads.
|
|
|
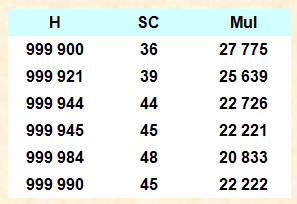
Liste
de grands nombres HARSHADS 999 900 < N <
1000 000 |
|
|
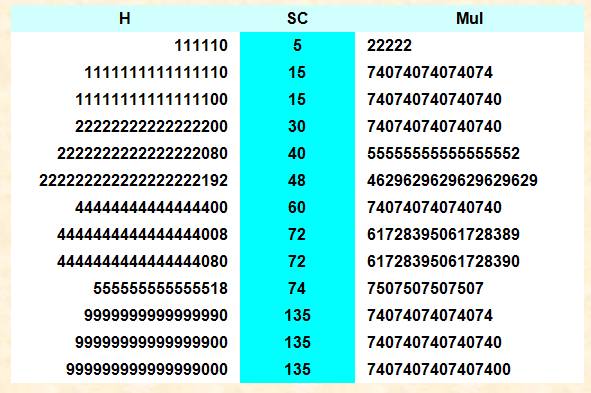
Effectivement beaucoup moins de nombres harshad dans
les plages de nombres sans chiffre zéro. Et, une somme de chiffres qui croît (ici > 36)
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/HarshadQ.htm |
![]()