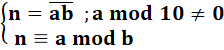|
Édition du: 24/08/2020 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
NOMBRES MODESTES |
||
|
|
Sommaire de cette page >>> Approche et définition >>> Nombres modestes – Listes >>> Nombres modestes au sens étendu – Records |
Débutants Glossaire |
|
Prenons le nombre 763.
Les chiffres du nombre se retrouvent tous dans la division
euclidienne hors le quotient. La
première présentation est triviale. Un nombre, divisé par 10, a toujours pour
reste son chiffre des unités. |
Voir Modulo |
|
|
Définition Un nombre n est modeste si on peut le partager en deux
parties a et b
et si n divisé par a donne un reste b. Sont
exclus les a finissant en 0 qui produisent
des présentations triviales. |
|
|
|
Nombres modestes (colonne de
gauche) La colonne de gauche montre la liste des vrais
modestes, car les chiffres dans la division euclidienne sont dans l'ordre de
ceux du nombre. Ce sont les nombres
définis comme modestes dans la liste OEIS A054986. Dans cette colonne, les nombres en rouge me
semblent illicites car ce sont des solutions triviales. Il est évident, par
exemple, que 111 = 10 x 11 + 1. Nombres modestes étendus (colonnes
en jaune) Dans les quatre colonnes en jaune, on trouve
toutes les solutions de divisibilités quel que soit l'ordre des chiffres.
Rappel en rouge de ceux dans le bon ordre. En jaune foncé, les cas de
répétitions. À noter que même dans la liste officielle, on
trouve les nombres avec des zéros implicites comme 103 pour lequel il faut
noter l'opération: 103 mod 03 = 1 pour
avoir tous les chiffres. |
|||||
|
|
13, 3, 1 19, 9, 1 23, 3, 2 |
26, 6, 2 29, 9, 2 39, 9, 3 |
46, 6, 4 49, 9, 4 59, 9, 5 |
69, 9, 6 79, 9, 7 89, 9, 8 |
|
|
Nombres de Suite de cette liste en Aplenty |
103, 03, 1 105, 15, 0 108, 18, 0 109, 09, 1 128, 18, 2 130, 3, 1 133, 33, 1 148, 18, 4 152, 21, 5 162, 12, 6 168, 18, 6 168, 81, 6 190, 9, 1 199, 99, 1 203, 03, 2 206, 06, 2 209, 09, 2 211, 11, 2 217, 27, 1 217, 72, 1 218, 18, 2 230, 3, 2 231, 12, 3 233, 33, 2 247, 27, 4 260, 6, 2 266, 66, 2 271, 12, 7 281, 21, 8 290, 9, 2 297, 72, 9 299, 99, 2 309, 09, 3 310, 3, 1 311, 11, 3 |
316, 63, 1 320, 3, 2 326, 36, 2 327, 27, 3 371, 13, 7 379, 93, 7 381, 18, 3 386, 63, 8 390, 9, 3 399, 99, 3 405, 45, 0 406, 06, 4 409, 09, 4 411, 11, 4 412, 12, 4 418, 18, 4 422, 22, 4 433, 33, 4 435, 54, 3 436, 36, 4 460, 6, 4 462, 24, 6 466, 66, 4 490, 9, 4 495, 54, 9 499, 99, 4 509, 09, 5 511, 11, 5 521, 12, 5 527, 75, 2 533, 33, 5 561, 15, 6 572, 27, 5 581, 18, 5 590, 9, 5 |
594, 45, 9 599, 99, 5 609, 9, 6 611, 11, 6 613, 36, 1 618, 18, 6 620, 6, 2 622, 22, 6 627, 27, 6 633, 33, 6 640, 6, 4 651, 15, 6 653, 36, 5 654, 54, 6 679, 96, 7 690, 9, 6 693, 36, 9 699, 99, 6 702, 27, 0 703, 37, 0 709, 09, 7 711, 11, 7 721, 21, 7 732, 27, 3 733, 33, 7 745, 57, 4 762, 27, 6 763, 36,
7 763, 63, 7 781, 18, 7 790, 9, 7 791, 17, 9 792, 27, 9 799, 99, 7 809, 09, 8 |
811, 11, 8 812, 12, 8 822, 22, 8 824, 24, 8 831, 18, 3 833, 33, 8 836, 36, 8 844, 44, 8 851, 18, 5 866, 66, 8 871, 18, 7 872, 27, 8 872, 72, 8 890, 9, 8 891, 18, 9 899, 99, 8 910, 9, 1 911, 11, 9 912, 21, 9 920, 9, 2 921, 12, 9 927, 27, 9 930, 9, 3 933, 33, 9 934, 49, 3 940, 9, 4 950, 9, 5 954, 45, 9 960, 9, 6 970, 9, 7 980, 9, 8 981, 18, 9 981, 81, 9 983, 39, 8 |
|
Nombres modestes au sens étendu – Records de
quantités de présentations
De 100 à 1000 000
|
Lecture; 168 est le plus petit nombre n
avec deux présentations (Q = 2):
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |