NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Diviseurs
Débutants Diviseurs Débutants Nombres parfaits	Types de nombres selon leurs diviseurs			Glossaire Diviseurs
INDEX Décomposition Diviseurs	Abondant …	Économes …	Parfait	Sublimes
		Sommaire de cette page >>> Approche >>> Premières valeurs >>> Conjecture de Dickson >>> Nombres frugaux >>> Nombres équidigitaux >>> Nombres prodigues ou extravagant

Nombres ÉCONOMES, FRUGAUX

ÉQUIDIGITAUX et

PRODIGUES ou EXTRAVAGANTS

Classement selon la quantité de chiffres pour écrire le nombre et ses facteurs premiers.

Approche
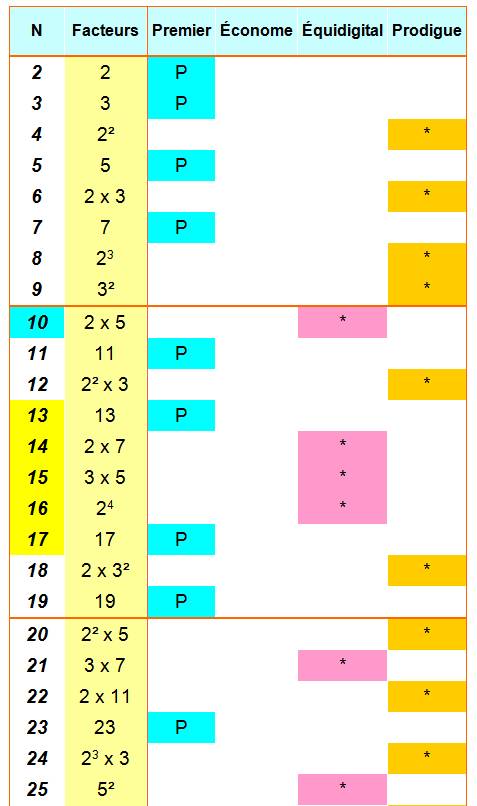
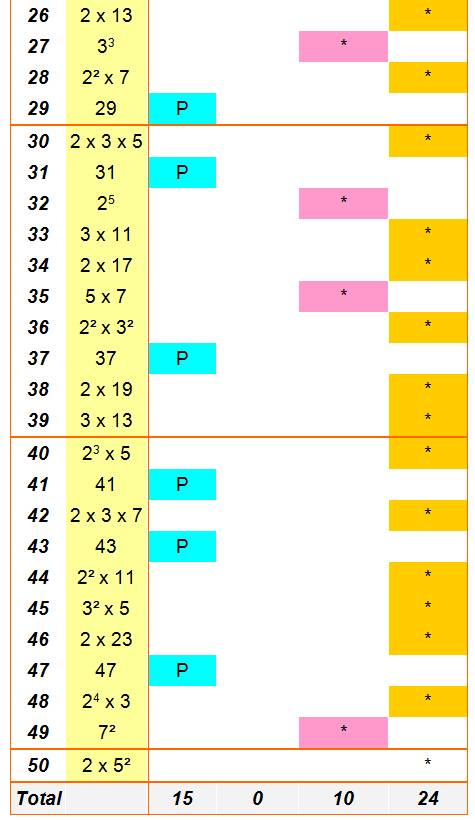
On compte le nombre de chiffres pour écrire les facteurs et on compare au nombre de chiffres du nombre lui-même. Le facteur 1 initial est ignoré. Les exposants différents de 1 sont coptés. Nombres récemment introduit par Bernardo Recamàn Santos.
Économes / Economical		Prodigue ou extravagant Wasteful or Extravagant
Frugal / Frugal	Équidigital / Equidigital
125 = 5^3	10 = 2 x 5	4 = 2²
1024 = 2^10	49 = 7²	26 = 2 x 13
Moins de chiffres	Même nombre de chiffres	Plus de chiffres
>>>	>>>	>>>
À rapprocher des nombre simples au sens de Kolmogorov, définis en considérant le moyen de codage le plus économique qui représente un nombre.

Approche – Premières valeurs
Les nombres premiers sont tous équidigitaux (47 = 1 x 47, soit 47 en excluant le facteur 1) 10 est le premier véritable équidigital (en excluant les nombres premiers). 13, 14, 15, 16 et 17: première chaîne de 5 premiers nombres économes successifs. Il n'existe pas de nombres économes inférieurs à 100. Le plus petit est 125. De 157 à 163, on trouve 7 entiers économes successifs (R. Pinch)

Suite et tables en Nombres économes ou frugaux

CONJECTURE DE DICKSON

Énoncée en 1904, non démontrée. Pour toute suite ai et bi (i = 1,...,k d'entiers), il existe une infinité de valeurs de n telles que tous les nombres (a1n + b1), (a2n + b2), ..., (akn + bk) soient simultanément des nombres premiers, sauf s'il existe un entier d qui, pour tout n, divise le produit (a1n + b1)(a2n + b2)...(akn + bk). Pour k égal à 1, la conjecture indique que, si les nombres a1n + b1 ne sont pas tous multiples d'un même nombre d quand n varie, alors il existe une infinité de nombres premiers de la forme a1n + b1 Démontrée cette conjecture, permettrait de dire que: les nombres premiers jumeaux sont en nombre infini; les nombres composés 2^n - 1, avec n premier, sont en nombre infini ; etc. Théorème de Dirichlet: Cas particulier de la conjecture de Dickson pour k = 1. 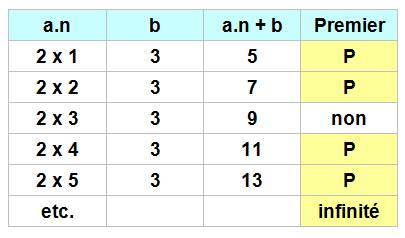Si a et b sont premiers entre eux, alors il existe une infinité de nombres premiers de la forme a.n + b Exemples: 2 et 3 sont premiers entre eux R.Pinch (1998) À partir ce cette conjecture, il montre qu'il existe des suites de nombres économes consécutifs aussi longues que l'on veut de même que pour les nombres prodigues.

Nombres frugaux Frugal numbers
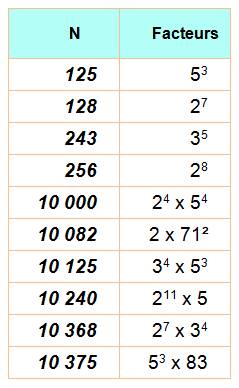
Nombre qui a plus de chiffres que ceux de sa factorisation, exposants supérieurs à 1 compris. Ex: 125 = 5^3	125, 128, 243, 256, 343, 512, 625, 729, 1024, 1029, 1215, 1250, 1280, 1331, 1369, 1458, 1536, 1681, 1701, 1715, 1792, 1849, 1875, 2048, 2187, 2197, 2209, 2401, 2560, 2809, 3125, 3481, 3584, 3645, 3721, 4096, 4374, 4375, 4489, 4802, 4913, 5041, 5103, 5329, 6241, 6250, 6561, 6859, 6889, 7203, 7921, 8192, 9375, 9409, 10000, 10082, 10112, 10125, 10201, 10206, 10240, 10368, 10375, 10443, 10449, 10496, 10609, 10624, 10625, 10633, 10658, 10752, 10935, 10976, 10985, 11008, 11045, 11125, 11163, 11392, 11421, 11449, 11664, 11767, 11776, 11875, 11881, 11907, 12005, 12032, 12125, 12167, 12288, 12393, 12416, 12482, 12500, 12544, 12691, 12769, 12800, 12879, 12943, 13122, 13125, 13467, 13568, 13718, 13778, 13824, 13851, 14045, 14063, 14336, 14337, 14375, 14406, 14641, 14739, 14749, 14823, 14848, 15104, … A046759
Sous condition de véracité de la conjecture des premiers jumeaux, Pinch a montré qu'il existe des suites de nombres économes consécutifs aussi longues que l'on veut. Une telle suite de neuf nombres commende par: 1 034 429 177 995 381 247. D'autres exemples avec sept nombres: 157, 108 746, 109 997, 121, 981, 142, 421.
English: Economical Number is a number N if the number of digits in the prime factorization of N (including powers) is less than the number of digits in N. The first few Economical numbers are: 125, 128, 243, 256, 343, 512, 625, 729, …

Nombres équidigitaux Equidigital numbers
Nombre qui a autant de chiffres que ceux de sa factorisation, exposants supérieurs à 1 compris. Ex: 16 = 2^4	1, 2, 3, 5, 7, 10, 11, 13, 14, 15, 16, 17, 19, 21, 23, 25, 27, 29, 31, 32, 35, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 105, 106, 107, 109, 111, 112, 113, 115, 118, 119, 121, 122, 123, 127, 129, 131, 133, 134, 135, 137, 139, 141, 142, 145, 146, 147, 149, 151, 155, 157, 158, 159, 160, 161, 162, 163, 166, 167, 169, 173, 175, 177, 178, 179, 181, 183, 185, 189, 191, 192, 193, 194, 197, 199, 201, 203, 205, 211, 213, 215, 217, 219, 223, 224, 227, 229, 233, 235, 237, 239, 241, 245, 249, 250, 251, 257, 259, 263, 265, 267, 269, 271, 277, 281, 283, 287, 289, 291, 293, 295, 301, 305, 307, 311, 313, 317, 320, 329, 331, 335, 337, 347, 349, 353, 355, 359, 361, 365, 367, 371, 373, 375, 379, 383, 384, 389, 395, 397, 401, 405, 409, 413, 415, 419, 421, 427, 431, 433, 439, 443, 445, 448, 449, 457, 461, 463, 467, 469, 479, 485, 486, 487, 491, 497, 499, 503, A046758
Suite de

Nombres prodigues ou extravagant Wasteful ot extravagant numbers
Nombre qui a moins de chiffres que ceux de sa factorisation, exposants supérieurs à 1 compris. Ex: 30 = 2 x 3 x 5	4, 6, 8, 9, 12, 18, 20, 22, 24, 26, 28, 30, 33, 34, 36, 38, 39, 40, 42, 44, 45, 46, 48, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 108, 110, 114, 116, 117, 120, 124, 126, 130, 132, 136, 138, 140, 143, 144, 148, 150, 152, 153, 154, 156, 164, 165, 168, 170, 171, 172, 174, 176, 180, 182, 184, 186, 187, 188, 190, 195, 196, 198, 200, 202, 204, 206, 207, 208, 209, 210, 212, 214, 216, 218, 220, 221, 222, 225, 226, 228, 230, 231, 232, 234, 236, 238, 240, 242, 244, 246, 247, 248, 252, 253, 254, 255, 258, 260, 261, 262, 264, 266, 268, 270, 272, 273, 274, 275, 276, 278, 279, 280, 282, 284, 285, 286, 288, 290, 292, 294, 296, 297, 298, 299, 300, 302, 303, 304, 306, 308, 309, 310, 312, 314, 315, 316, 318, 319, 321, 322, 323, 324, 325, 326, 327, 328, 330, 332, 333, 334, 336, 338, 339, 340, 341, 342, 344, 345, 346, 348, 350, 351, 352, 354, 356, 357, 358, 360, 362, 363, 364, 366, 368, 369, 370, 372, 374, 376, 377, 378, 380, 381, 382, 385, 386, 387, 388, 390, 391, 392, 393, 394, 396, 398, 399, 400, 402, 403, 404, 406, 407, 408, 410, 411, 412, 414, 416, 417, 418, 420, 422, 423, 424, 425, 426, 428, 429, 430, 432, 434, 435, 436, 437, 438, 440, 441, 442, 444, 446, 447, 450, 451, 452, 453, 454, 455, 456, 458, 459, 460, 462, 464, 465, 466, 468, 470, 471, 472, 473, 474, 475, 476, 477, 478, 480, 481, 482, 483, 484, 488, 489, 490, 492, 493, 494, 495, 496, 498, 500, 501, … A046760

Wasteful: gaspilleur, dépensier

Suite	Nombres parfaits Nombres selon diviseurs Voir haut de page
Voir	Calcul mental – Index Géométrie – Index Nombres économes, équidistants et prodigues Tables abondants / déficients Théorie des nombres – Index
Sites	Les chasseurs de nombres premiers – Jean-Paul Delahaye – Un chapitre concerne les nombres économes et les nombres prodigues. Nombre frugal – Wikipédia Economical numbers – Wolfram MathWorld Economical numbers – The Prime Glosary Economical numbers – Numbers Aplenty Economical numbers – Geeks for Geeks – Programmation Nombre équidigital – Wikipédia Equidigital – Geeks for Geeks – Programmation Equidigital – Numbers Aplenty Nombre extravagant – Wikipédia Wasteful numbers – Numbers Aplenty Wasteful numbers – Geeks for Geeks – Programmation
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Econome.htm