nombres fourchettes ou gapful

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 06/12/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Nombres	NOMBRES de HARSHAD et voisins				Glossaire Chiffres
INDEX Décomposition Types de nombres	Harshad =>	Présentation	Listes	Curiosités
	Nus =>	Présentation	Nombres nus	Zuckerman
	Insolite =>	Présentation
	Chiffres =>	Fourchette	Divise-Chiffres
		Sommaire de cette page >>> Nombres fourchettes: (x…y) / xy – GAPFUL >>> Nombres fourchettes retournés: (x…y) / yx >>> Nombres fourchettes doubles: (xu…vy) / xuvy >>> Nombres trappes: (xu…y) / x…y >>> Anglais

Nombres FOURCHETTES

Gapful numbers et voisins

Propriété des nombres face à la division par ses chiffres.

Nombre divisibles par le nombre formé par ses chiffres extrêmes; autrement-dit: divisible par lui-même après avoir supprimé les chiffres de son centre.

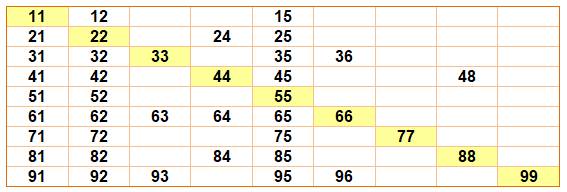
Nombres à deux chiffres divisibles par le chiffre de leurs unités

Exemple: 63 se termine par 3 et il est divisible par 3.

NOMBRES FOURCHETTES: (x…y)/xy
Définition	Nombre qui est divisible par le nombre formé avec les chiffres de ses extrémités. Les nombres divisibles par 10 sont ignorés (cas triviaux. Ex: 1230 est divisible par 10). Les nombres dits "gapful" inclut les divisibles par 10.
Exemples	105 / 15 = 7 315 = 35 x 9
Remarque	De 100 à 999, on trouve une majorité de cas où le quotient est 11. En effet, dans ce cas) la multiplication par 11 conserve les deux chiffres extrêmes tout en plaçant la somme au centre. Exemple: 594 = 11 x 54 et 594 est divisible par 54.
Propriété	Aucun nombre de trois chiffres n'est divisible par le nombre formé par les centaines et les dizaines. xyz n'est pas divisible par xy, en revanche, il peut être divisible par xz (c'est alors un nombre fourchette). Voir Nombres trappes

Liste

de 100

à 999

(44)

Ex: 105 / 15 = 7 devient [105, 15, 7]

[105, 15, 7], [108, 18, 6], [121, 11, 11], [132, 12, 11], [135, 15, 9], [143, 13, 11], [154, 14, 11], [165, 15, 11], [176, 16, 11], [187, 17, 11], [192, 12, 16], [195, 15, 13], [198, 18, 11], [225, 25, 9], [231, 21, 11], [242, 22, 11], [253, 23, 11], [264, 24, 11], [275, 25, 11], [286, 26, 11], [297, 27, 11], [315, 35, 9], [341, 31, 11], [352, 32, 11], [363, 33, 11], [374, 34, 11], [385, 35, 11], [396, 36, 11], [405, 45, 9], [451, 41, 11], [462, 42, 11], [473, 43, 11], [484, 44, 11], [495, 45, 11], [561, 51, 11], [572, 52, 11], [583, 53, 11], [594, 54, 11], [671, 61, 11], [682, 62, 11], [693, 63, 11], [781, 71, 11], [792, 72, 11], [891, 81, 11].

Liste

de 1000

à 1999

(118)

[1001, 11, 91], [1005, 15, 67], [1008, 18, 56], [1032, 12, 86], [1035, 15, 69], [1037, 17, 61], [1053, 13, 81], [1056, 16, 66], [1064, 14, 76], [1065, 15, 71], [1092, 12, 91], [1095, 15, 73], [1098, 18, 61], [1111, 11, 101], [1125, 15, 75], [1134, 14, 81], [1136, 16, 71], [1152, 12, 96], [1155, 15, 77], [1159, 19, 61], [1183, 13, 91], [1185, 15, 79], [1188, 18, 66], [1204, 14, 86], [1207, 17, 71], [1212, 12, 101], [1215, 15, 81], [1216, 16, 76], [1221, 11, 111], [1245, 15, 83], [1272, 12, 106], [1274, 14, 91], [1275, 15, 85], [1278, 18, 71], [1296, 16, 81], [1305, 15, 87], [1313, 13, 101], [1331, 11, 121], [1332, 12, 111], [1335, 15, 89], [1344, 14, 96], [1349, 19, 71], [1365, 15, 91], [1368, 18, 76], [1376, 16, 86], [1377, 17, 81], [1392, 12, 116], [1395, 15, 93], [1414, 14, 101], [1425, 15, 95], [1441, 11, 131], [1443, 13, 111], [1452, 12, 121], [1455, 15, 97], [1456, 16, 91], [1458, 18, 81], [1484, 14, 106], [1485, 15, 99], [1512, 12, 126], [1515, 15, 101], [1536, 16, 96], [1539, 19, 81], [1545, 15, 103], [1547, 17, 91], [1548, 18, 86], [1551, 11, 141], [1554, 14, 111], [1572, 12, 131], [1573, 13, 121], [1575, 15, 105], [1605, 15, 107], [1616, 16, 101], [1624, 14, 116], [1632, 12, 136], [1635, 15, 109], [1638, 18, 91], [1661, 11, 151], [1665, 15, 111], [1692, 12, 141], [1694, 14, 121], [1695, 15, 113], [1696, 16, 106], [1703, 13, 131], [1717, 17, 101], [1725, 15, 115], [1728, 18, 96], [1729, 19, 91], [1752, 12, 146], [1755, 15, 117], [1764, 14, 126], [1771, 11, 161], [1776, 16, 111], [1785, 15, 119], [1812, 12, 151], [1815, 15, 121], [1818, 18, 101], [1833, 13, 141], [1834, 14, 131], [1845, 15, 123], [1856, 16, 116], [1872, 12, 156], [1875, 15, 125], [1881, 11, 171], [1887, 17, 111], [1904, 14, 136], [1905, 15, 127], [1908, 18, 106], [1919, 19, 101], [1932, 12, 161], [1935, 15, 129], [1936, 16, 121], [1963, 13, 151], [1965, 15, 131], [1974, 14, 141], [1991, 11, 181], [1992, 12, 166], [1995, 15, 133], [1998, 18, 111]

NOMBRES FOURCHETTES retournés: (x…y)/yx
Définition	Nombre qui est divisible par le nombre formé avec les chiffres de ses extrémités dans l'ordre inverse. Les nombres divisibles par 10 sont ignorés
Exemple	164 / 41 = 4
Liste de 100 à 999 (20)	[121, 11, 11], [164, 41, 4], [242, 22, 11], [294, 42, 7], [322, 23, 14], [344, 43, 8], [351, 13, 27], [363, 33, 11], [432, 24, 18], [484, 44, 11], [644, 46, 14], [688, 86, 8], [702, 27, 26], [703, 37, 19], [731, 17, 43], [812, 28, 29], [816, 68, 12], [864, 48, 18], [931, 19, 49], [966, 69, 14]

NOMBRES FOURCHETTES doubles: (xu…vy)/xuvy
Définition	Nombre qui est divisible par le nombre formé avec les deux chiffres de ses extrémités. Les nombres divisibles par 10 sont ignorés. Les nombres produisant un quotient 101 sont ignorés.
Exemple	104 275 / 1075 = 97
Remarque	Ils sont tous avec un quotient 97 ou 105.
Liste pour n de 10⁵ à 10⁶ (20)	[104275, 1075, 97], [107625, 1025, 105], [113975, 1175, 97], [118125, 1125, 105], [123675, 1275, 97], [128625, 1225, 105], [133375, 1375, 97], [139125, 1325, 105], [143075, 1475, 97], [149625, 1425, 105], [152775, 1575, 97], [162475, 1675, 97], [172175, 1775, 97], [181875, 1875, 97], [191575, 1975, 97], [201275, 2075, 97], [210975, 2175, 97], [220675, 2275, 97], [230375, 2375, 97], [240075, 2475, 97], …
Trivial	[101101, 1001, 101], [101202, 1002, 101], [101303, 1003, 101], [101404, 1004, 101], [101505, 1005, 101], [101606, 1006, 101], … Ils sont très nombreux.
Cas de (x..vy) / xvy (Nombreux)	[10032, 132, 76], [10065, 165, 61], [10098, 198, 51], [10125, 125, 81], [10336, 136, 76], [10625, 125, 85], [10675, 175, 61], [10935, 135, 81], [10944, 144, 76], [11125, 125, 89], [11248, 148, 76], [11285, 185, 61], [11375, 175, 65], [11552, 152, 76], [11625, 125, 93], [11745, 145, 81], [11856, 156, 76], [11895, 195, 61], …
Analyse numérique	Un seul chiffre initial et central a = 1, b = 25 N = 10000 + 100x + 25 d = 100 + 25 On cherche: x pour N = qd 10000 + 100x + 25 = 100q + 25q x = (125q – 10025) / 100 Une tabulation montre que: x = 89, 93 et 97 En effet: 11125 / 125 = 89 11625 / 125 = 93 12125 / 125 = 97	Deux chiffres centraux a = 10, b = 75 N = 10000 + 100x + 75 d = 10000 + 75 On cherche: x pour N = qd 10000 + 100x + 75 = 1000q + 75q x = (1075q – 100075) / 100 Une tabulation montre que: x = 97, 101 Seul 97 a deux chiffres. Seule solution: 104275 / 1075 = 97

NOMBRES TRAPPES (xu…y) / x…y
Définition	Nombre, non multiple de 10, qui est divisible par lui-même en ayant omis un chiffre quelconque, sauf celui- de tête. Ex: pour 1234, on cherche la divisibilité par 123, 124 ou 134.
Exemple	105 / 15 = 7 1625 / 125 = 13
Propriété	Parmi toutes les possibilités, le seul diviseur est celui avec le deuxième chiffre éliminé (mis à la trappe). Exemple avec 1625, les diviseurs possibles sont: 162, 165, 125; seul 125 est un diviseur.
Liste de 100 à 999 (44)	[105, 15, 7], [108, 18, 6], [121, 11, 11], [132, 12, 11], [135, 15, 9], [143, 13, 11], [154, 14, 11], [165, 15, 11], [176, 16, 11], [187, 17, 11], [192, 12, 16], [195, 15, 13], [198, 18, 11], [225, 25, 9], [231, 21, 11], [242, 22, 11], [253, 23, 11], [264, 24, 11], [275, 25, 11], [286, 26, 11], [297, 27, 11], [315, 35, 9], [341, 31, 11], [352, 32, 11], [363, 33, 11], [374, 34, 11], [385, 35, 11], [396, 36, 11], [405, 45, 9], [451, 41, 11], [462, 42, 11], [473, 43, 11], [484, 44, 11], [495, 45, 11], [561, 51, 11], [572, 52, 11], [583, 53, 11], [594, 54, 11], [671, 61, 11], [682, 62, 11], [693, 63, 11], [781, 71, 11], [792, 72, 11], [891, 81, 11] Ce sont les mêmes que les nombres fourchettes à trois chiffres
de 1000 à 10 000 (10)	[1125, 125, 9], [1575, 175, 9], [1625, 125, 13], [2025, 225, 9], [2475, 275, 9], [2925, 225, 13], [3375, 375, 9], [4275, 475, 9], [5175, 575, 9], [6075, 675, 9]
de 10⁴ à 10⁵ (17)	[10125, 1125, 9], [12375, 1375, 9], [14625, 1625, 9], [16875, 1875, 9], [19125, 1125, 17], [21375, 2375, 9], [23625, 2625, 9], [25875, 2875, 9], [30375, 3375, 9], [32625, 3625, 9], [34875, 3875, 9], [41625, 4625, 9], [43875, 4875, 9], [50625, 5625, 9], [52875, 5875, 9], [61875, 6875, 9], [70875, 7875, 9]
de 10⁴ à 10⁵ (1)	[180625, 10625, 17], le plus grand !

Anglais

Gapful Number is a number N of at least 3 digits such that it is divisible by the concatenation of it’s first and last digit.

Few Gapful Numbers are: 100, 105, 108, 110, 120, 121, 130, 132, 135, 140,…

Gapful signifie béant en anglais.

Voir Anglais pour le bac et pour les affaires

Suite	Liste de nombres de Harshad Nombres insolites Nombres k fois la somme de ses chiffres Racine numérique Nombres de Kaprekar Jeux avec somme des chiffres
Voir	Carré magique avec des nombres nus Nom des nombres Nombres économes, équidigitaux, prodigues Théorie des nombres Calcul mental Géométrie Type de nombres selon ses diviseurs
Sites	Un chiffre à la trappe – Diophante.fr Gapful numbers – Numbers Aplenty OEIS A308237 - Numbers m not ending with 0 that contain a digit, other than the leftmost digit, that can be removed such that the resulting number d divides m OEIS A108343 - Gapful numbers >= 100: numbers that are divisible by the number formed by their first and last digit. Numbers up to 100 trivially have this property and are excluded OEIS A034837 - Numbers that are divisible by first digit OEIS A178157 - Numbers n that are divisible by every prefix of n Gapful numbers – Geekforgeek – Programmation Python (et autres) Gapful numbers – Rosetta code – Programation Python (et autres)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Fourche.htm