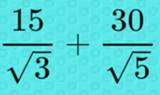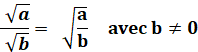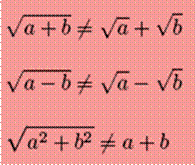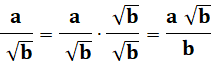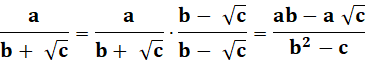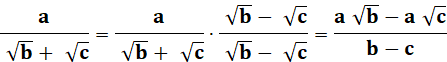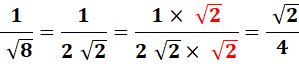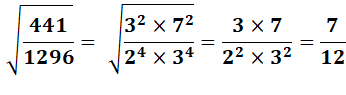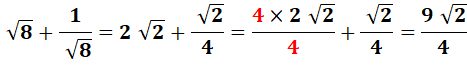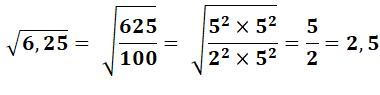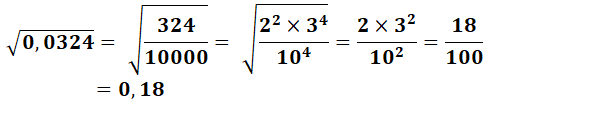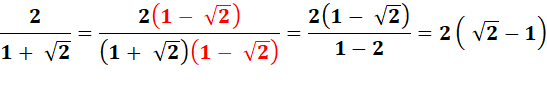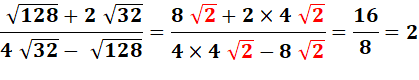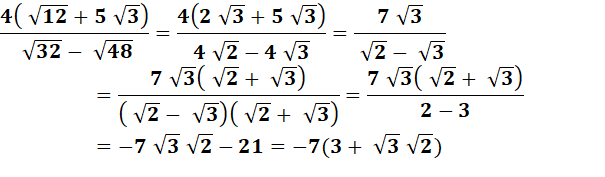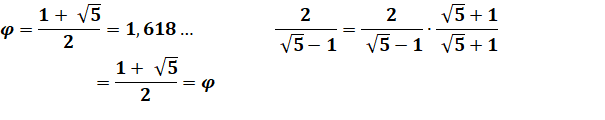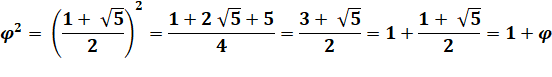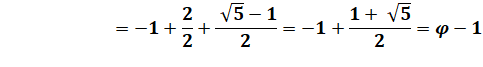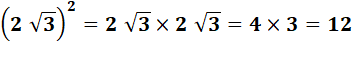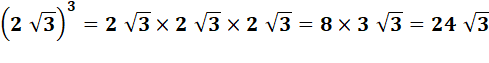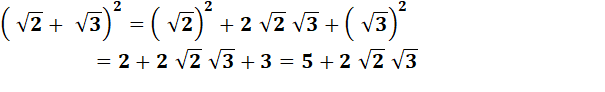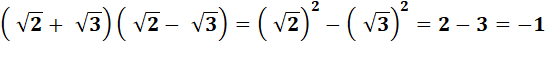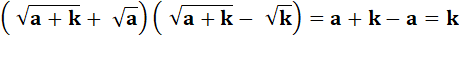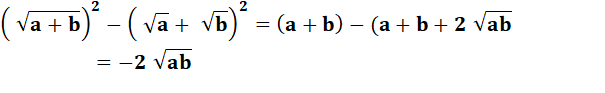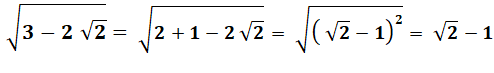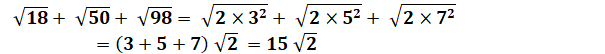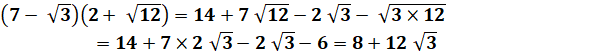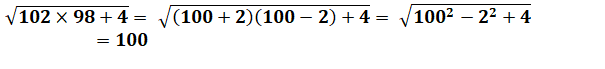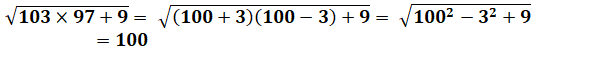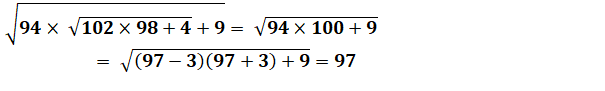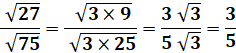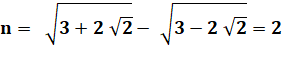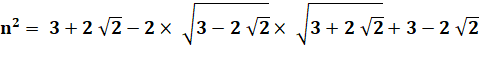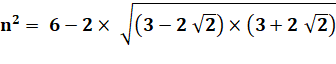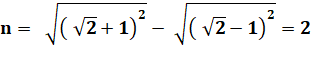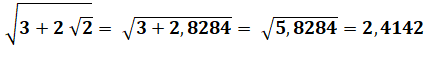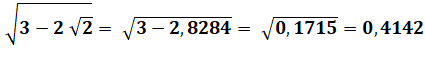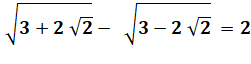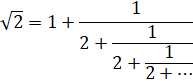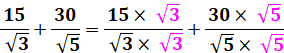|
||||||||||||||||||||||||||||||||||||
![]()
|
RACINE CARRÉE Exemples de calculs avec les radicaux Le
radical Un
élève de seconde doit connaitre les méthodes de calcul exposées dans cette
page |
Voir Enseignement – Index
|
Calculez
|
|
Définition |
|
|
|
C |
Voir
Toutes
les formules |
|
|
Attention |
|
|
|
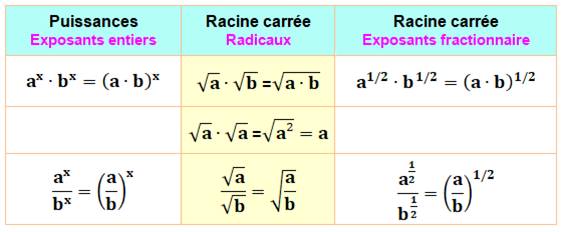
Comparaison Mêmes règles de
calcul que pour les puissances Une racine est
en fait une puissance fractionnaire. |
|
|
|
Dénominateur
sans radical Multiplier par
la fraction des conjugués (qui vaut 1) |
|
|
|
|
||
|
Les quatre opérations |
|
|
|
Sous le radical |
Et pas son opposé: Car ce symbole implique: racine carrée positive
|
|
|
Piège! |
= 2 x 14142 … = 2,8284…
2,2360 … 1,4142… + 1, 7320… = 3,1462
|
|
|
Positif et négatif |
|
|
|
Fractions |
|
|
|
Rationnels |
|
|
|
Exemples de calcul avec le nombre d'or
|
![]()
|
Puissances
Développements et
applications d'identités
remarquables
Détection d'identités
remarquables
Voir Calcul impossible?
/ Application au
calcul de tg (Pi/8) Calcul numérique
|
|
Exercices
|
|
Voir Racines en équations
/ Racines en
fractions / Radicaux et Maple
Voir aussi Pièges de calcul / Fractions / Puissances / Identités
/ Calculs avec des racines
cubiques
|
|
||
|
1)
Montrez que: |
|
|
|
Au carré |
|
|
|
Calcul |
|
|
|
Identité remarquable |
|
|
|
Retour au nombre |
|
|
|
2)
On aurait pu faire Voir Autre
exemple ci-dessous |
|
|
|
3)
Calcul arithmétique pour comparer |
|
|
Exemple avec radical sous radical:
qrt(2+sqrt(3))

Pour info
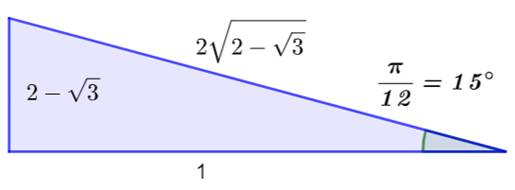
Voir Angle
pi/12
Exemple de calcul d'une racine de racines
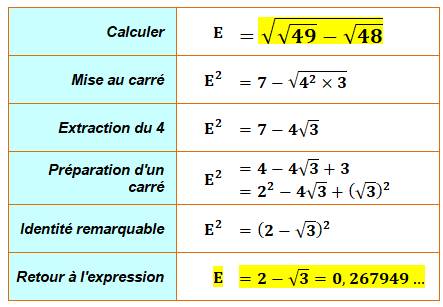
Voir Brève 58-1148
Autre exemple: 4*sqr(4-2*sqrt(3))+sqrt(97-56*sqrt(3))

Voir Brève
733
|
Bon
à savoir |
|
En effet:
|
||
|
Irr |
Sauf si le nombre est un
carré parfait, la racine est un nombre irrationnel. Voir Démonstration |
|||
|
Fr |
|
Noté:
[1 ;
2, 2, 2, 2, 2, 2, 2, 2...] Voir Autres
valeurs / Équation de Pell |
||
|
Curiosité |
Observation Considérons la valeur
entière de la racine des nombres successifs:
Observez le passage à la
valeur entière suivante. La taille des marches de l'escalier (en bleu) est la
suite des nombres impairs! Explication Le passage à la nouvelle
valeur entière apparaît lorsqu'on atteint un carré parfait. Or, d'un carré parfait au
suivant, on peut écrire la relation suivante (a + 1)² – a² = a² + 2a +
1 – a² = 2a + 1 Cette différence
représente exactement les nombres impairs successifs. |
|||
|
Calculez
|
|
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
||
|
Cette page |
||
![]()