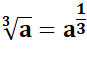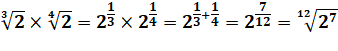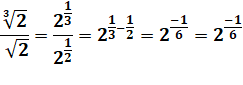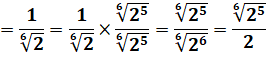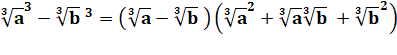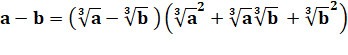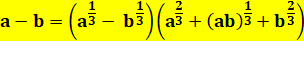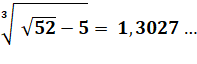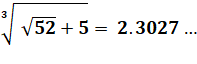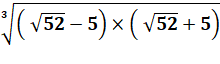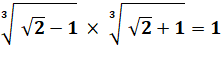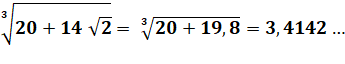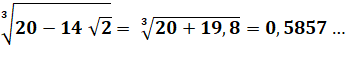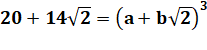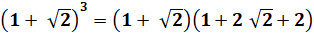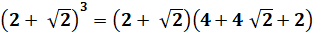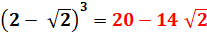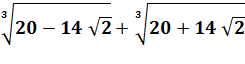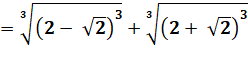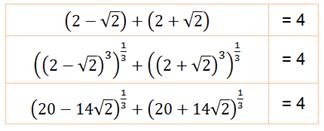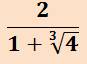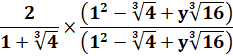NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Mathématiques
Débutants Général	Calcul avec radicaux			Glossaire Général
INDEX Racines Calculs Calcul mental	Racine carrée	Racine cubique	Racines des complexes
	Lycée	Sommaire de cette page >>> Calculs de base >>> Identité avec les racines cubiques >>> Produit de racines cubiques conjuguées >>> Somme de racines cubiques conjuguées >>> Suppression radical au dénominateur

Calculs algébriques avec radicaux

Puissances fractionnaires

Quelques exemples typiques.

Calculs
Écriture fractionnaire
Exemple avec produit
Exemple avec fraction

Voir Simplification sous radicaux – Brève 59-1161 / Calcul de (2/3)^(2/3)

Identité avec les racines cubiques
Différence de cubes
Posons
L'égalité devient
Simplification à gauche
Écriture fractionnaire

Voir Identités remarquables / Application

PRODUIT:
Écriture Vous trouverez aussi cette formulation (écriture traitement de texte).		(52^(1/2)-5)^1/3x(52^(1/2)+5)^1/3
Calcul numérique Avec une calculette on vérifie cette égalité.		Leur produit = 3
Calcul algébrique La racine cubique s'applique en fait à l'ensemble du produit
Identité remarquable (a – b)(a + b) = a² - b²
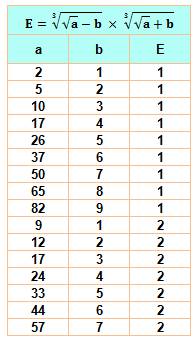
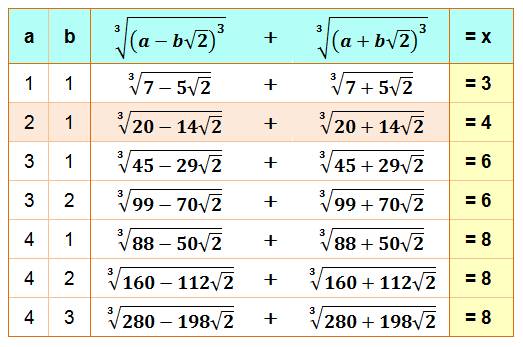
Alternatives Ce tableau montre quelques autres possibilités pour ce type d'égalité. La plus petite étant:

SOMME:
Écriture Vous trouverez aussi cette formulation (écriture traitement de texte).		(20-14x2^(1/2))^1/3+(20+14x2^(1/2))^1/3
Calcul numérique Avec une calculette on vérifie cette égalité		Leur somme = 4
Calcul algébrique Avant de penser à une identité remarquable, voyons si les termes sous racine ne sont pas des cubes.		Le développement sera en a^3 + … Avec a^3 < 20 a = 1 ou 2 et b du même ordre
Recherche d'un cube Essayons a = b = 1
Essayons a = 2 et b = 1 Bon choix!
Est-ce bon aussi pour son conjugué? Tous calculs faits, c'est bon!
Notre expression devient alors:
Commentaires Il semble évident que l'auteur de cette question l'a composé à l'envers
Alternatives Ce tableau montre quelques autres possibilités pour ce type d'égalité.

FRACTION:
Écriture Vous trouverez aussi cette formulation (écriture traitement de texte).		(20-14x2^(1/2))^1/3+(20+14x2^(1/2))^1/3
Calcul numérique Avec une calculette:
Problème	On cherche à éliminer le radical au dénominateur. La méthode classique du conjugué, utilisée avec les racines carrées, ne marche pas. Notez que la méthode s'applique si le signe est négatif au dénominateur; prendre l'identité remarquable avec les signe moins.
Calcul algébrique Différence de cubes, en prenant a = 1 et b = racine cubique de 4 Mise en évidence de notre dénominateur.
En multipliant notre fraction
En reprenant l'égalité trouvée au dénominateur

Voir Radicaux et Maple

Suite	Voir haut de page
Voir	Calcul – Index Radicaux avec Maple P8 = f(P4)
Cette page	http://villemin.gerard.free.fr/aMaths/ARITALGE/Radicaux.htm