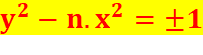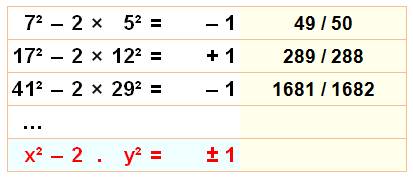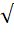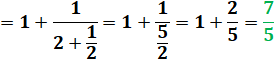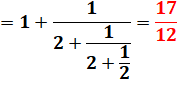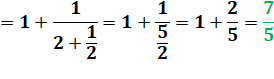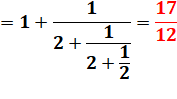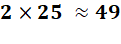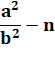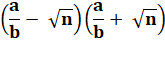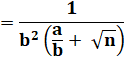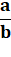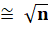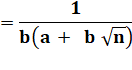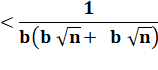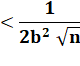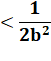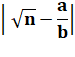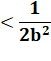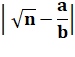|
|||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATION DE PELL-FERMAT
|
Exemple historique
|
32 188 120 829 134 849² – 313 x 1 819 380 158 564 160² = 1 |
|
|
1657: William Brouncker trouve les relations qui
relient la fraction
continue d'un nombre quadratique à l'équation de Pell-Fermat. Bernard Frénicle résout l'équation pour n
jusqu'à 150. Il défie Brouncker de trouver la
solution pour n = 313 tout en précisant que lui, il l'a trouvée en quelques
heures. |
|
|
|
||
|
Quels
sont les carrés égaux au double d'un autre à un près? Exemple 5²
= 25 Son
double = 50 Or
7² = 49 = 50 – 1 Note: Il est possible de
généraliser à m près. |
|
|
|
|
||
|
Une
équation diophantienne
ne comporte que des coefficients entiers. Une
équation de Pell-Fermat est une équation diophantienne de la forme indiquée,
avec n positif et non carré. |
Équation de Pell
Exemple 3²
= 2 x 2² + 1 |
|
Suite Exemples
d'équations de Pell
|
|
||||
|
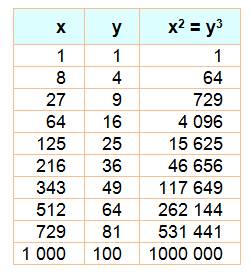
Équation de Pell en cube et carré. x² = y3
+ 1 Cette équation sous une forme ou une autre
ne possède qu'une seule solution avec les nombre 8 et 9. Équation
de Catalan. |
3² = 23 + 1 23 = 3² – 1 |
|||
|
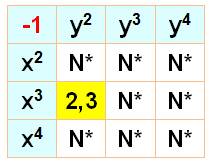
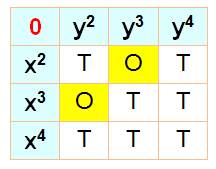
Par contre, cette
équation de Pell n'a pas de solution x² =
y² + 1 Les tableaux montrent les autres
possibilités d'équations, toutes sans solution sauf celle en x2 et
y3. |
Exemple
de lecture x² = y² + 1 => N (Non), aucune solution.
* hors solution
trivi |
|||
|
En passant
de 1 à 0. x3
= y² + 0 Solutions
possible avec cube = carré. Solutions
également évidentes: tous les y sont des carrés: y = t² => x² =
(t²)3 & x = t3 |
|
T = trivi O = oui,
solutions; voir ci-contre |
||
|
|
||
|
Lorsqu'on
cherche quels sont les carrés égaux au double d'un autre à un près, on fait
appel à un merveilleux outil mathématique: les fractions continues. |
|
|
|
En
l'occurrence la fraction continue de racine
de 2. Lorsque la fraction continue est tronquée, la fraction
correspondante est appelée réduite de racine de 2. |
|
|
|
Miracle ou
magie! Numérateur et dénominateur sont solutions de l'équation de Pell. |
N² – 2D² = |
|
|
Fraction
continue de racine de 2: |
|
|
|
Voici les quatre premières réduites de racine de 2. Anglais: convergents. |
(1) |
|
|
(2) |
|
|
|
(3) |
|
|
|
(4) |
|
|
Exemples de solutions de
l'équation de Pell. Il y en a une infinité.
Elles alternent en positif et négatif; positives lorsque le dénominateur est
pair. |
1² – 2 x 1² |
= –1 |
|
3² – 2 x 2² |
= 1 |
|
|
7² – 2 x 5² |
= –1 |
|
|
17² – 2 x 12² |
= 1 |
Les réduites de racines de 2 et vérification de l'équation de
Pell
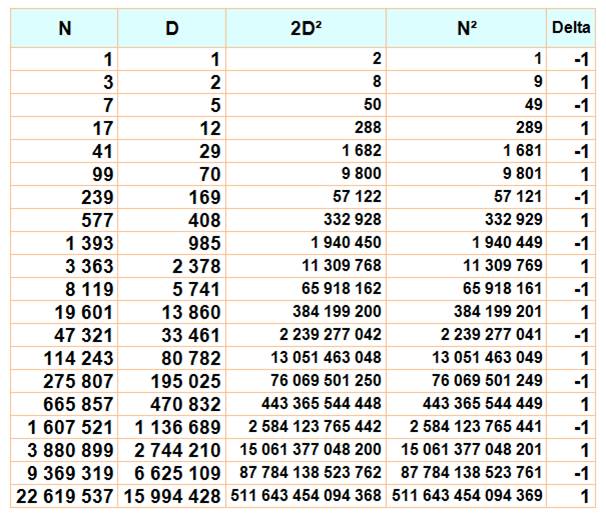
Voir Tables des réduites
|
|
|||||
|
Que les
réduites donnent des valeurs proches, nous n'en sommes pas très étonnés. Le
théorème de la meilleure approximation dit que: Si la
réduite s'écrit N/D, alors l'écart entre ce nombre rationnel et le nombre
irrationnel qu'elle représente est inférieur à 1/D². |
Écart
selon le théorème: 1/25 = 0,04 |
||||
|
La
différence est extrêmement petite |
|||||
|
Si nous
disposons d'une solution avec a et b. |
a² – n.b² |
= 1 |
|||
|
En
divisant par b²: |
|
|
|||
|
|
|
||||
|
En
divisant par le 2e facteur: |
|
|
|||
|
Le
deuxième membre est très petit, surtout si b est grand. |
|
= très petit |
|||
|
La
fraction est très voisine de la racine de n. |
|
|
|||
|
Pourquoi
une solution de l'équation de Pell est une réduite de racine de n? |
|||||
|
Soit a et
b une solution: |
a² – n.b² |
= 1 |
|||
|
Développement: |
(a – b |
= 1 |
|||
|
En
divisant par le 2e facteur |
(a – b |
|
|||
|
Le
dénominateur est positif |
(a – b |
> 0 |
|||
|
Soustraction
du 2e terme |
a |
> b |
|||
|
Calculons
cette expression, en multipliant en haut et en bas par le conjugué |
|
|
|||
|
Reprenons
notre inégalité |
|
|
|||
|
|
|
|
|||
|
En diminuant
le dénominateur, on augmente la valeur de la fraction. |
|
|
|||
|
C'est
précisément la condition pour que a/b soit une
réduite de racine de n. |
|
|
|||
|
Les
solutions de cette équation sont les paires (numérateur / dénominateur) des
réduites de racine de n. Cette
page montrait l'exemple pour n = 2. |
Voir Énigme du numéro de la villa comme
belle application
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()