|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Rectangles magiques avec nombres répétés
Exemple |
Anglais: Magic rectangle with repetition of numbers
|
|
||
|
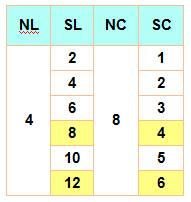
Condition sur les constantes
magiques La somme
de tous les nombres du rectangle (S) est
égale à la somme de toutes les lignes (SLL) et aussi à la somme de
toutes les colonnes (SCC)
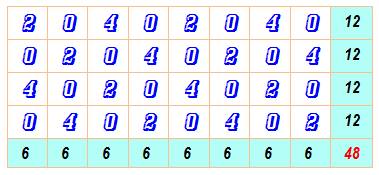
Tout rectangle magique avec répétitions (RMrep) devra respecter cette condition sous
peine d'être impossible à réaliser. Exemple avec les sommes
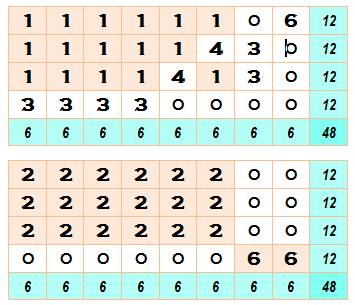
12 et 6, la grille comportera: (1 ligne et 2 colonnes) ou (2 lignes et 4
colonnes) ou (3 lignes et 6 colonnes) ou (4 lignes et 8 colonnes, exemple
ci-contre) ou etc. |
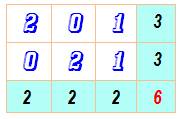
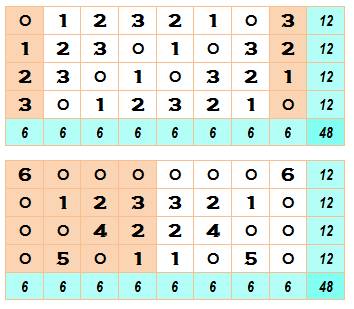
Exemple (trivial)
Partitions Les nombres sur une ligne constituent une partition
du nombre 12, et il y en a: 77 Les nombres sur une colonne constituent une partition du nombre 6, et il
y en a: 11 dont 9 avec quatre chiffes ou moins: [1,1,2,2], [2,2,2],
[1,1,1,3], [1,2,3], [3,3], [1,1,4], [2,4], [1,5], [6]. |
|
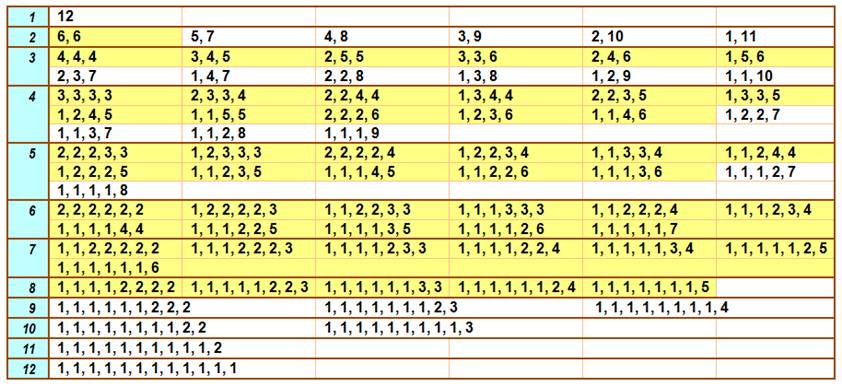
Les 77 partitions du nombre 12 selon
la quantité de termes
Pour la formation du rectangle 8 x 3, seules les 52
partitions notées en jaune sont recevables
(Pas plus de 8 termes et nombres de 0 à 6
seulement)
|
|
||
|
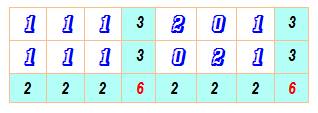
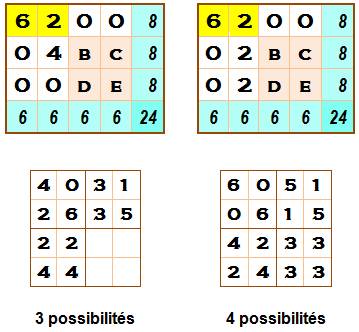
La somme
en colonne est 2; avec partitions possibles: [1, 1] et [2]. La somme
en ligne est 3; avec partitions possibles: [1, 1, 1], [2, 1], [3]. Le dernier
cas avec 3 est à éliminer car supérieur à la somme en colonne. |
Deux possibilités avec R3/2
Deux possibilités uniquement, hors les permutations; possibles avec le
rectangle de droite. |
|
|
|
||
|
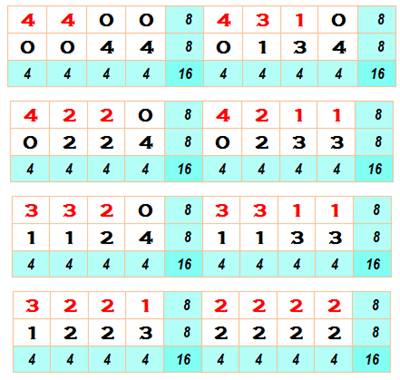
La somme
en colonne est 4; avec partitions possibles: [2, 2], [3,1] et [4]. La somme
en ligne est 8; avec les partitions possibles indiquées en rouge sur les
grilles ci-contre. Chacune
des partitions de 8 est portée sur la première ligne; le complément à 4 est
calculé pour compléter les colonnes. |
Huit possibilités avec R4/2 (hors permutations)
|
|
|
|
|||||||
|
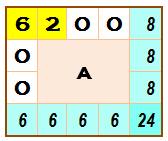
Paramètres Rectangle
4 x 3 Sommes: 6 et 8 Partitions Sachant
que chaque terme est au plus égal à 6 et que pour 6 il y a trois termes au
maximum et pour 8, quatre au maximum. |
Partitions recevables
|
||||||
|
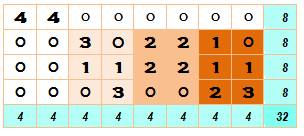
Partition 8 = 6 + 2 Testons
la première colonne et la première ligne avec 600 et 6200 A = 3 x 6
– 2 = 16 = 2 x 8 = 16 Sous-rectangle
A: faisable |
|
||||||
|
Sous-rectangle magique A À gauche,
partitions de 6 comprenant un 2: À droite,
partitions de 6 avec deux termes: Etc. |
|
||||||
|
Les
29 possibilités avec 6200 et 600 dont 10 primitives (les autres s'en
déduisent par permuttaions)
Avec les
autres configurations en première ligne et première colonne, il y a 8 623
rectangles magiques RMrep 8 x 3, y compris les permutations. |
|||||||
|
|
||
|
Choix
des sommes Le rectangle est faisable tant que nous
respectons la formule:
|
Nous choisissons d'étudier les deux cas: |
|
|
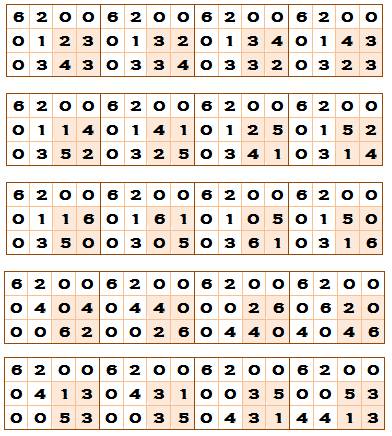
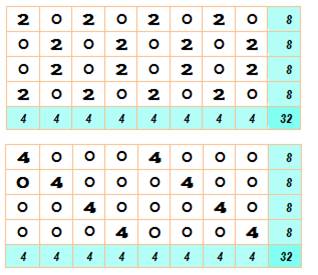
Somme 8 et 4 La grille
remplies de 1 est magique. Ci-contre
deux spécimens de RMrep 8 x 4. Exemple
de construction Choisissez des partitions de 8 ou de 4 et de vérifiez que celles-ci ne
font pas déborder la somme en ligne et en colonne. Vérifiez également que les
sommes pourront bien être atteintes.
On
comprend aisément qu'il existe une multitude de choix possibles. Soit des
milliers de RMrep 8 x 4 avec sommes 8 et 4. |
Deux
rectangles parmi les plus simples
Exemple
de construction
La mise sur tableur de cette grille peut vous faciliter la recherche de
tels rectangles. |
|
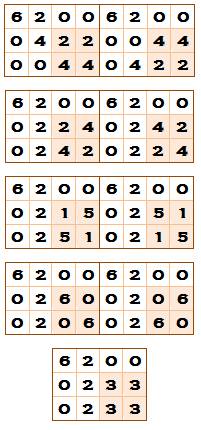
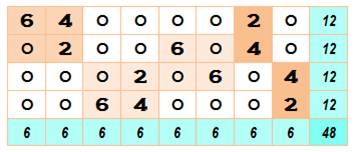
Somme 12 et 6 Comme on
peut s'y attendre la quantité de tels rectangles est très grande (plusieurs
milliers). |
Exemple de
construction
|
|
Maximum de 1
ou maxium de 2
|
Symétries
avec nombres de 0 à 3, puis de 0 à 6
|
Estimation de la quantité de RMrep
|
La programmation directe du calcul de la quantité est
relativement simple; par contre, le temps de calcul est rédhibitoire sans
trouver le moyen d'accélérer le processus. Prenons les cas du carré 8 x 4 avec somme 12 et 6, il y a
neuf partitions du nombre 6 et pour chacune un certain nombre de
combinaisons; tout compte fait, cela fait 78 types de colonnes à prendre 8
par 8. Ce qui donne:
Potentiellement 23 milliards de rectangles magiques. Avec
le rectangle 4 x 3, le programme donne 8 623 RMrep pour 3 108 105
explorations soit un ratio de réussite égal à 360. |
|
On comprend pourquoi
la littérature tout comme Internet ne parlent pas
beaucoup de ce type de rectangle magique.
Il est possible d'en construire autant que l'on en veut. Sans doute un
bon divertissement. |
|
|
||
|
|
Commentaires Positionnement d'un compteur de succès (kt). Ouverture du package logiciel combinatoire. Liste des cinq partitions du nombre 4 avec quatre termes. Listes des permutations (PPj) et quantité de permutations
dans chacune (qPPj). Boucle de choix de la première colonne avec j1 parmi les cinq
partitions et k1 pour une des permutations de cette partition. Notez l'emploi de la double barre de concaténation qui permet de faire
évoluer le nom des listes. Boucles pour les sept autres colonnes. Calcul de la somme sur les quatre lignes (L1, L2, L3 et L4). Pas
besoin de calculer sur les colonnes puisque nous utilisons une partition de
cette somme. Si les quatre sommes de lignes sont égales à 8, alors progression du
compteur kt. Pas d'impression car beaucoup trop et saturation assurée de
l'ordinateur. Fin des 2 x 8 boucles. L'exécution de ce programme exige plusieurs dizaines d'heures de
calcul. La principale piste pour réduire considérablement cette durée
d'exécution serait d'éliminer rapidement les configurations redondantes. Une
autre piste serait de procéder par sous rectangles emboités. |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/RecRepet.htm
|
![]()