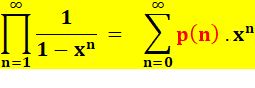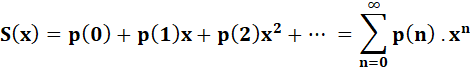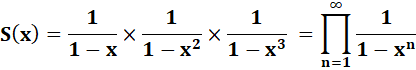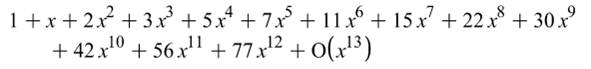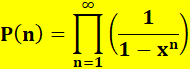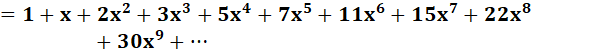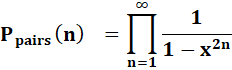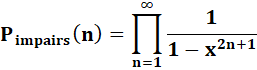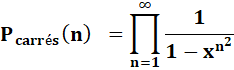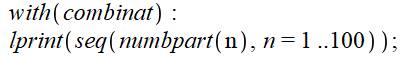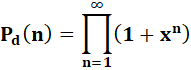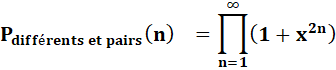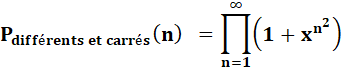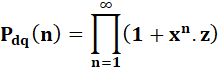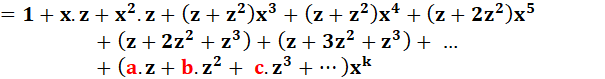|
||||||||||||||||||||||||||||||||||||||||
![]()
|
FONCTIONS GÉNÉRATRICES des QUANTITÉS de PARTITIONS des
NOMBRES Nous
savons qu'une fraction polynomiale simple
engendre tous les nombres entiers. Existe-t-il
une telle fraction qui donnerait des renseignements sur les partitions des
nombres? OUI, elle existe, mais la formule se
complique juste un petit peu. Fonction génératrice
d'Euler et son théorème
Voyons
cela pas à pas… |
|
|
|
|
Euler montre
l'égalité des deux séries suivantes:
Développement pour n = 5 S(x) = 1 + x +
2x2 + 3x3 + 5x4 + 7x5
Exemple de calculs jusqu'à 6
En jaune, le développement pertinent compte tenu
du nombre de facteurs dans le produit. Nous reconnaissons bien la quantité de
partitions. Voici le développement pour n = 16
Le O(x13) final indique que le terme
suivant sera en puissance 13. Utilisation Nous allons utiliser cette relation et des
semblables pour dénombrer les partitions: complète ou alors avec sommants
diiférents. |
|
Voir Identité
d'Euler avec les nombres premiers / Identités
classiques / k-bonacci et partitions
|
|
|||||
|
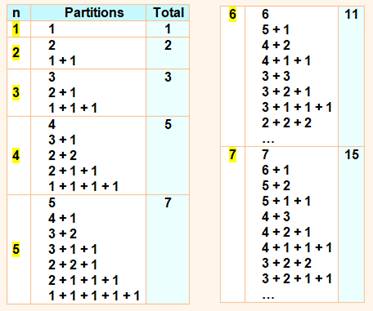
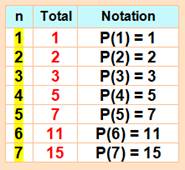
Dénombrement Nous
nous intéressons aux partitions
des nombres: toutes les sommes possibles sans se préoccuper des permutations
des nombres (1 + 2 et 2 + 1 comptent pour une seule partition. Constituons la table qui donne la quantité de partitions
des nombres de 1 à 7 Par exemple, pour le
nombre 6, il ya 11 sommes possibles: P(6) = 11. |
Quantité
de partitions des nombres de 1 à 7
|
||||
|
En
résumé |
|
||||
|
Polynôme
générateur Prenons le polynôme
suivant: Développons en sachant
que le calcul peut se faire en se souvenant que
(pour x proche de 0):
1 / (1 – x2) = 1 + x2
+ x4 + x6 + x8 +… 1 / (1 – x3) = 1 + x3
+ x6 + x9 +… Conservons les
premiers monômes en les ordonnant selon le degré de x (en
rouge à droite). Comparez les
coefficients obtenus aux nombres du tableau des partitions ci-dessus.
Identique! C'est Euler qui a
découvert cette relation. |
= 1 + 1 x1 + 2 x2 + 3 x3 + 5 x4 + 7 x5 + 11 x6 + 15 x7 + 22 x8 + 30 x9 + 42 x10 etc. |
||||
|
Formule pour toutes les partitions Il existe donc un
polynôme qui, une fois développé, donne la quantité des partitions Les coefficients de ce
polynôme indiquent la quantité de partitions du nombre exposant de x. P(9) =
30. |
|
||||
|
Généralisation |
|
||||
|
Programme
MAPLE Les quantités de partitions des cent
premiers nombres |
1, 2, 3,
5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627,
792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, 6842, 8349, 10143,
12310, 14883, 17977, 21637, 26015, 31185, 37338, 44583, 53174, 63261, 75175,
89134, 105558, 124754, 147273, 173525, 204226, 239943, 281589, 329931,
386155, 451276, 526823, 614154, 715220, 831820, 966467, 1121505, 1300156,
1505499, 1741630, 2012558, 2323520, 2679689, 3087735, 3554345, 4087968,
4697205, 5392783, 6185689, 7089500, 8118264, 9289091, 10619863, 12132164,
13848650, 15796476, 18004327, 20506255, 23338469, 26543660, 30167357,
34262962, 38887673, 44108109, 49995925, 56634173, 64112359, 72533807,
82010177, 92669720, 104651419, 118114304, 133230930, 150198136, 169229875,
190569292 … |
||||
|
|
||||||||||||||||||||||||||||||||||||
|
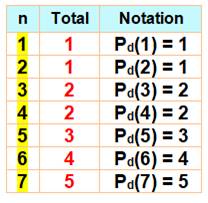
Dénombrement Nous
nous intéressons aux partitions
des nombres et plus particulièrement aux partitions formées de nombres tous différents. Constituons la table qui donne la quantité de partitions
en nombres différents des nombres de 1 à 7 Par exemple 6
se décompose en
Soit Pd(6) = 4 Bilan
|
|
|||||||||||||||||||||||||||||||||||
|
Polynôme
générateur Prenons le polynôme
suivant: Développons en
ordonnant les monômes selon le degré de x Comparez les
coefficients obtenus aux nombres du tableau des partitions ci-dessus Identique! C'est encore Euler qui
a découvert cette relation. |
(1
+ x) (1 + x2) (1 + x3) … (1 + x8) 1 + 1 x1 + 1 x2 + 2 x3 + 2 x4 + 3 x5 + 4 x6 + 5 x7 Tableau limité à x7 |
|||||||||||||||||||||||||||||||||||
|
Formule
pour des partitions formées de nombres différents Il existe un polynôme
qui, une fois développé, donne la quantité des
partitions formées de nombres différents |
|
|||||||||||||||||||||||||||||||||||
|
Généralisation |
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
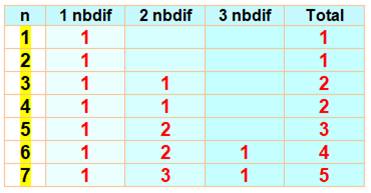
Dénombrement Reprenons
le tableau des partitions en distinguant la quantité de nombres utilisés pour
chaque partition et en repérant les cas avec un, deux ou trois nombres
différents. Constituons
la table qui donne la quantité de telles partitions pour les nombres de 1 à 7
Construisons
la table des quantités:
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Polynôme
générateur Prenons le polynôme
suivant: Développons en
ordonnant les monômes selon le degré de x en ligne et de z en colonne. Comparez les
coefficients obtenus aux nombres du tableau des partitions ci-dessus Identique! C'est encore Euler qui a
découvert cette relation. |
(1 + xz) (1 + x2z)
(1 + x3z) … (1 + x8z) 1 + 1 x1 . z1 + 1 x2 . z1 + 1 x3 . z1 + 1 x3 . z2 + 1 x4 . z1 + 1 x4 . z2 + 1 x5 . z1 + 2 x5 . z2 + 1 x6 . z1 + 2 x6 . z2 + 1 x6 . z3 + 1 x7 . z1 +
3 x7 . z2
+ 1 x7 . z3 Tableau
limité à x7 |
||||||||||||||||||||||||||||||||||||||||||
|
Formule
pour des partitions formées de nombres différents Il existe un polynôme qui, une fois
développé, donne la quantité des
partitions formées de nombres différents. Les coefficients (a, ,
c …) indiquent la quantité de partitions du nombre k en exactement (a, b, c
…) nombres différents. |
|
||||||||||||||||||||||||||||||||||||||||||
Voir Partitions strictes (avec nombre différents)
Bilan
|
Nous avons mis en correspondance des fractions qui
développées donnent les quantités de partitions des nombres. Ces formules sont intéressantes sur le plan des
mathématiques, mais le calcul pour un nombre n, surtout s'il est grand, est
fastidieux Hélas, il n'existe pas de formule donnant immédiatement le
résultat. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()