|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ESCALIER
qui mène à FIBONACCI Décomposition d'un entier sous
contraintes (1/2) Qui l'eut cru? Lorsque vous
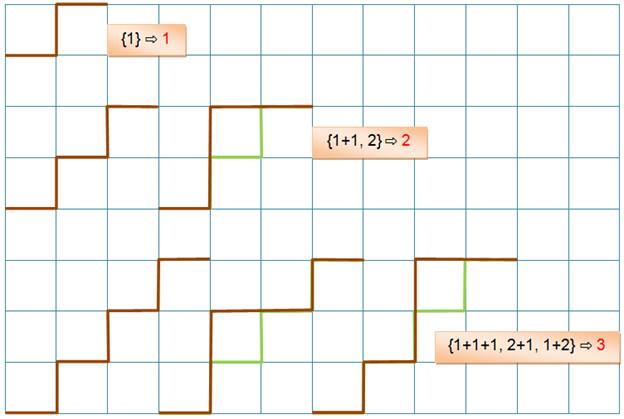
montez les marches d'un escalier en progressant d'une ou deux marches à la
fois, vous expérimentez la suite des nombres de Fibonacci sans le savoir. Voici l'énigme classique à
résoudre: Un escalier compte 5 marches. Je monte les marches par une ou par
deux. Combien de possibilités? Moyen imagé de compter les
façons de décomposer un nombre en sommes de termes avec la contrainte de
n'utiliser que des nombres allant de 1 à k, comme 5 = 1 + 2 + 2. |
Petit point de situation
|
Cette page et la suivante
traite de la décomposition partielle des
nombres: partitions avec permutation avec
les nombres de 1 à k seulement. S'agissant des
partitions (vraies, sans permutation), on rappelle la propriété importante
des partitions partielles: la quantité de partitions avec k sommants est
égale à celle des partitions avec le nombre k. Ce n'est pas le cas
avec les compositions. Mais, deux propriétés sont à noter:
|
Voir Partitions – Orientation – Petit
narratif avec liens sur ces pages
![]()
|
|
|
|
{deux fois 1 marche (21)
et une fois 2 marches (12)
};
|
|
|
|
||||||||||||||||||||||
|
Récapitulatif:
Suppléments
= quantité de possibilités en plus pour une marche de plus. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
En
fait, ce sont les toutes les combinaisons
de deux objets (ici le nombre 2) parmi quatre objets:
En vert, la simplification que l'on
effectue immédiatement avec un peu d'habitude. On peut voir les choses aussi avec les permutations: permuter quatre
objets: 4!. Mais les deux 1 donnent des permutations identiques: 2! C'est la
même chose pour les 2 qui donnent 2! permutations à éliminer. Soit le bilan:
4!/ (2! x 2!) = 1 x 2 x 3 x 4 / 4 = 6.
ou permutations: 5! / (3! x 2!) = 10.
ou permutations: 6! / (3! x 3!) = 4 x 5 x 6 / 6 = 20. |
|
|
|
|
|
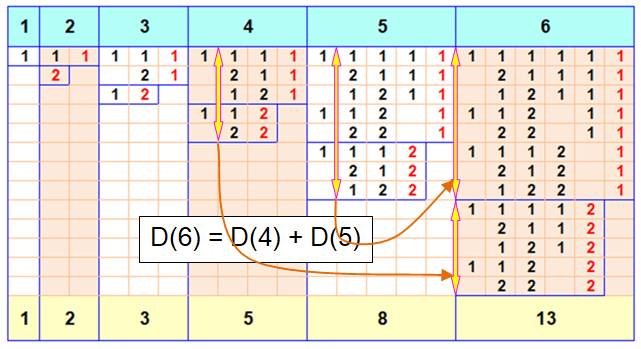
Ce tableau présente les compositions des nombres de 1 à 6:
partitions avec autorisation des permutations. On se limite aux additions avec les nombres 1 et 2
exclusivement. Voyez la construction: 1. Recopiez
la composition précédente et ajoutez 1; 2. Recopiez
la composition d'avant et ajoutez 2.
Pour le nombre 6: On retrouve toutes les compositions du 5 en ajoutant 1. Facile! Ensuite, pami toutes ces nouvelles combinaisons, il est possible de
remplacer les deux 1 finaux par un seul 2. Or, c'est la même quantité que
pour le 4 à laquelle on a ajouté 1 pour faire le 5, puis 1 pour faire le 6. Soit la formule générale: D(n + 1) = D(n) +
D(n–1) C'est typiquement la formule de récurrence de la construction des
nombres de Fibonacci. |
|
|
Le problème de la montée des n marches d'un escalier est équivalent à celui de la composition
(partition avec permutations) du nombre n. Avec la montée de 1 ou 2 marches à la fois – ou la
composition avec des 1 et 2 exclusivement – la quantité de possibilités est
égale au nombre de rang n+1 de la suite de Fibonacci.
Que
se passe-t-il si je pouvais monter aussi trois marches? >>> Donnez-moi
les conclusions, tout de suite >>> |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()