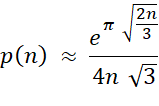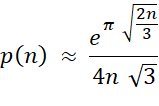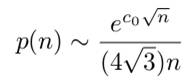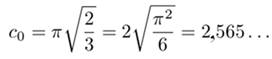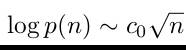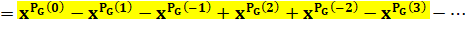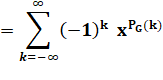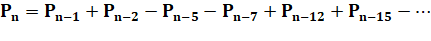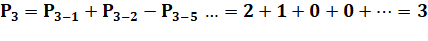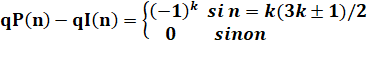![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PARTITION - Quantité Décomposition d'un nombre en sommes de nombres. Combien ? Formule ? P(n) est la quantité de partitions du nombre entier n
Par définition: P(0) = 1 et
P(n<0) = 0 Historique te point des recherches Euler
s'est intéressé le premier à la partition des nombres, notamment avec sa fonction
génératrice. Savoir ce que devient P(n) pour n grand a beaucoup intrigué les
mathématiciens. Hardy, Ramanujan et Rademacher tentèrent de donner des formules d'approximation de P(n). Encore aujourd'hui, on ne sait pas décider si P(n) est pair ou
impair. Un sujet souvent traité consiste à trouver des identités (bijections) entre sous-ensembles
de partitions. Le diagramme de Ferrers
s'est avéré un précieux outil. |
|
|
Voir Types de partitions
Voir NUMBER
OF PARTTIONS – Calculateur en ligne – dcode
|
|
|||
|
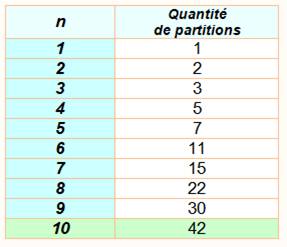
On peut compter les partitions ou se
référer à une liste établie (Tableau). Voir
l'encyclopédie des suites de nombres: A000041
– a(n) = number of partitions of n (the partition numbers). |
|
||
|
Avoir recours à un logiciel de
calcul mathématique: Exemple
avec Maple et son logiciel
spécialisé: combinat
(combinatoire). L'instruction numbpart fournit immédiatement la quantité de
partitions. L'instruction
seq
demande de calculer la même chose pour n de 1 à 30. |
|
||
|
Faire une division de polynôme. |
|
||
|
Conclusions |
Pas facile
de dénombrer les partitions d'un nombre
entier ! >>> Par contre, compter les compositions (partitions, y compris les
permutations) est assez simple >>> |
||
|
|
|||
|
Dénombrement Les compostions
sont toutes les partitions déclinées avec leurs permutations. La quantité de
compositions pour partitionner n est: 2n-1. Toutes les partitions, permutations
comprises. |
Exemple 3 = 1 + 1 + 1 = 1 +
2 = 2 + 1 4 possibilités (dont le nombre
lui-même) Soit: 4 = 23 – 1 |
||
|
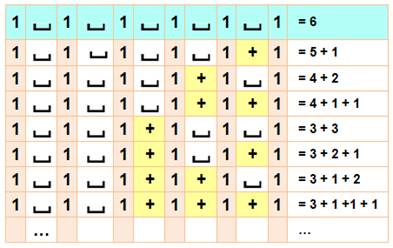
Démonstration Le nombre à
décomposer est écrit sous forme de bâtons: 6 = I I I I I I Les compositions
sont formée en plaçant le signe + ou le signe espace entre les "I"
de toutes les façons possibles: I I I + I I I représente 3 + 3. Pour le nombre n,
il y a n – 1 intervalles et donc 2n – 1 façons de placer les deux
symboles. |
|||
|
Exemple avec n = 6 Remarquez
qu'en plaçant 0 et 1 à la place des deux symboles "plus" et
"espace", on retrouve les nombres en binaire.
|
Compositions du nombre
6
D(6)
= 25 |
||
|
|
||
|
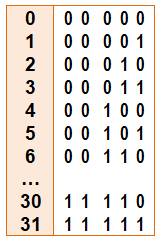
Quantité de partitions Il n'existe pas de
formule simple donnant la quantité p(n) de décompositions d'un nombre n en
somme de nombres, permutations exclues. Vers 1918, Ramanujan et Hardy trouvent une limite asymptotique
qui conduit à la formule:
Eux-mêmes, puis
d'autres comme Rademacher en 1937, donnèrent d'autres formules plus précises,
mais beaucoup plus compliquées. |
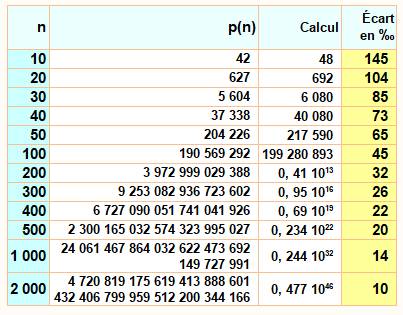
Que donne la formule ?
La
quantité de partitions croît vertigineusement. Plus
de 1040 dès le nombre 2 000. La
formule converge très lentement. Encore
10 pour 1000 (soit 1%) pour n = 2000. |
|
|
La quantité de partitions p(n) d'un nombre positif n satisfait la
formule asymptotique suivante:
Avec:
= 2,5650996603237281911… On en déduit que:
|
Hardy et Ramanujan et aussi Uspensky ont trouvé
cette formule indépendamment. Leurs démonstrations font usage des variables complexes et les fonctions modulaires. Plus tard, Erdös trouvera
une démonstration plus directe, mais … très ardue. Méthode appliquant une démonstration par induction à une
formule récursive. D'après Elementary
Methods in Number Theory - Melvyn B. Nathanson - Springer - 2000 |
|
|
|
||
|
Pentagonaux généralisés |
Les nombres pentagonaux généralisés
Les premiers de la liste: 0, 1, 2,
5, 7, 12, 15, 22, 26, 35, 40, … |
|
|
Polynôme générateur Relation
entre puissances successives et puissance en pentagonaux généralisés (PG) |
Ces nombres se trouvent impliqués ici, via leur polynôme
générateur.
On retrouve les nombres pentagonaux généralisés en exposant. Voir Développements de cette expression |
|
|
Théorème des nombres pentagonaux (Euler) |
Cette expression se trouve liée aux partitions des
nombres par:
|
|
|
Calcul des quantités de partitions par récurrence Note: P0 = 1 |
L'établissement de cette somme à partir de la relation
précédente n'est pas évidente. Une approche est proposée ci-dessous. Plus
d'explications sur les sites en rérérence. Exemples de calcul d'une partition à partir des précédentes.
|
|
Anglais Euler's Pentagonal Number Theorem
|
|
|||
|
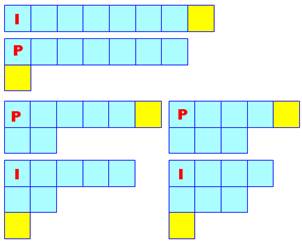
Parmi les
vingt-deux partitions du nombre 8,
seules six sont formées de nombres distincts: Leur diagramme
de Ferrers montre qu'il a autant
de partions avec une quantité paire de termes qu'impaire (notées P et I). Il est intéressant de noter que les couples se forment
en considérant un échange entre les carrés jaunes: carrés en bout droit (en
fait, la diagonale droite lorsqu'elle existe) contre les carrés de la base. |
Six partitions distinctes du nombre 8
|
||
|
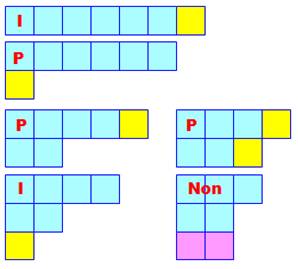
Parmi les
quinze partitions du nombre 7, seules cinq sont formées de nombres distincts: Leur diagramme de Ferrers montre que (impair oblige), les quantités P
et I sont différentes Deux couples sont formés. Pour la partition
restante (4 + 3), l'inversion de la diagonale droite contre la base conduit à
une partition (3 + 2 + 2) qui n'est plus en nombres distincts. |
Cinq partitions distinctes du nombre 7
|
||
|
Propriété Il se
trouve que les nombres avec partitions distinctes non équilibrées
(paires/impaires) sont les nombres pentagonaux généralisés, comme l'avait
découvert Euler. |
Question Comment
interviennent ces partitions disctinctes dans le calcul de l'expression E
(vue ci-dessus) ? |
||
|
Développement de l'expression E Voyons la contribution au coefficient de x5 Comparons aux trois partitions distinctes de 5:
Bilan: un impair et deux pairs Avec ce nombre pentagonal, le bilan est
déséquilibré. |
(1 – x) (1 – x2) (1 – x3)
(1 – x4) (1 – x5)…
Bilan pour x5
|
||
|
Et avec x56 Comparons aux quatre partitions distinctes de x6:
Bilan: autant de pairs que d'impairs Avec ce nombre pentagonal, le bilan est
équilibré. Moralité: tous les x avec une puissance
disparaissent de E, sauf pour celles égale à
un pentagonal. |
(1 – x) (1 – x2) (1 – x3)
(1 – x4) (1 – x5) (1 – x6) …
Bilan pour x5
|
||
|
Théorème des partitions distinctes Quantité de partitions distinctes paires (qP) et
impaire (qI). Propriété énoncée par Legendre (1752-1833) |
|
||
![]()
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Tables – Index
![]()
|
Retour |
|
|
Suite |
|
|
|
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()